人教版 八年级数学上册 12.3 角平分线的性质 课时训练(word含答案)
文档属性
| 名称 | 人教版 八年级数学上册 12.3 角平分线的性质 课时训练(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 551.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




文档简介
人教版 八年级数学 12.3 角平分线的性质 课时训练
一、选择题
1. 用直尺和圆规作一个角的平分线,示意图如图,则能说明OC是∠AOB的平分线的依据是( )
A.SSS B.SAS C.AAS D.ASA
2. 如图,OC平分∠AOB,P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是( )
A.2 B.3 C.4 D.5
3. 如图,在直角坐标系中,AD是Rt△OAB的角平分线,点D的坐标是(0,-3),那么点D到AB的距离是 ( )
A.3 B.-3 C.2 D.-2
4. 如图,OP平分∠AOB,点P到OA的距离为3,N是OB上的任意一点,则线段PN的长度的取值范围为 ( )
A.PN<3 B.PN>3 C.PN≥3 D.PN≤3
5. (2019?张家界)如图,在中,,,,BD平分,则点D到AB的距离等于
A.4 B.3 C.2 D.1
6. 如图,已知.按照以下步骤作图:①以点为圆心,以适当的长为半径作弧,分别交的两边于,两点,连接;②分别以点,为圆心,以大于线段的长为半径作弧,两弧在内交于点,连接,;③连接交于点.下列结论中错误的是
A. B.
C. D.
7. 如图,平面上到两两相交的三条直线a,b,c的距离相等的点一共有( )
A.4个 B.3个 C.2个 D.1个
8. 如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于点H.若∠AFB=40°,则∠BCF的度数为( )
A.40° B.50° C.55° D.60°
二、填空题
9. 如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为________.
10. 如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=________°.
11. 如图,请用符号语言表示“角的平分线上的点到角的两边的距离相等”.
条件:____________________________________.
结论:PC=PD.
12. △ABC的周长为8,面积为10,若其内部一点O到三边的距离相等,则点O到AB的距离为________.
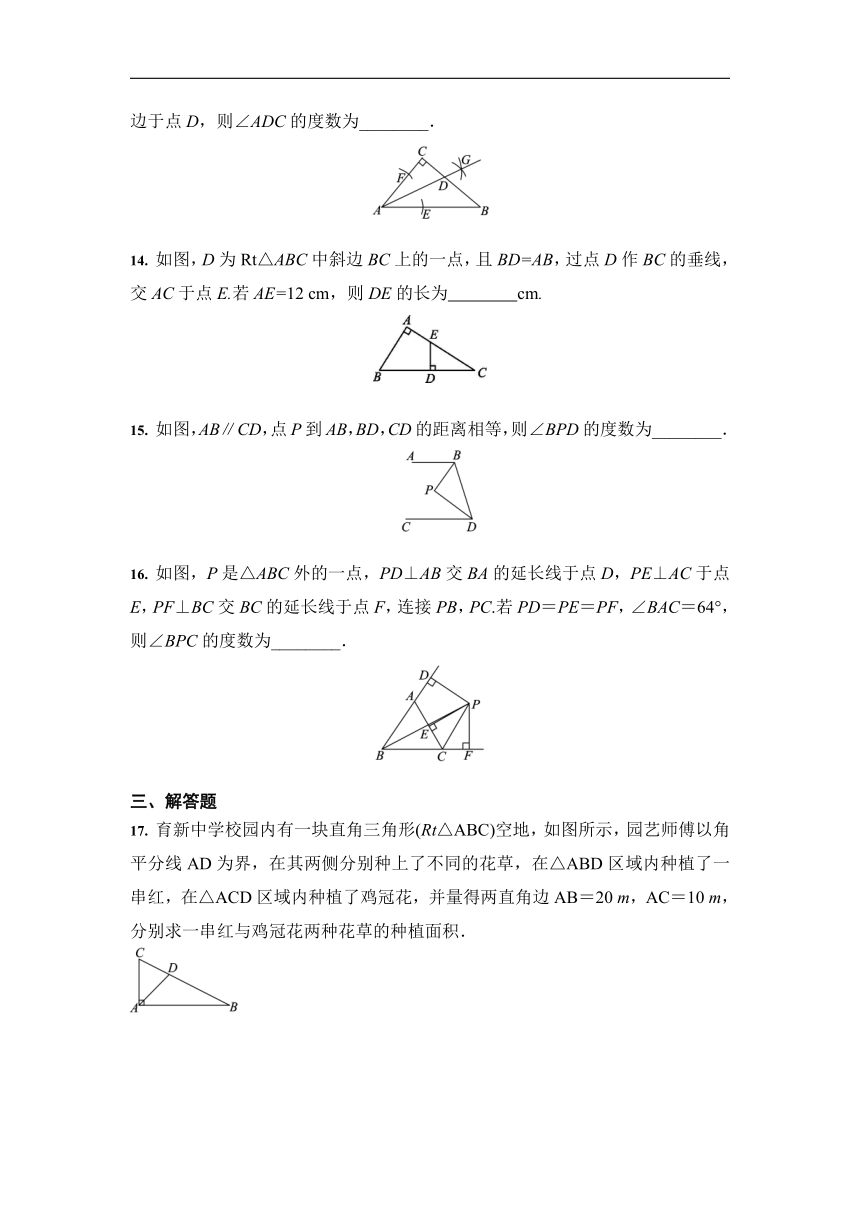
13. 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为________.
14. 如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12 cm,则DE的长为 cm.?
15. 如图,AB∥CD,点P到AB,BD,CD的距离相等,则∠BPD的度数为________.
16. 如图,P是△ABC外的一点,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,连接PB,PC.若PD=PE=PF,∠BAC=64°,则∠BPC的度数为________.
三、解答题
17. 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20 m,AC=10 m,分别求一串红与鸡冠花两种花草的种植面积.
18. 如图,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是142.5 cm2,AB=20 cm,AC=18 cm,求DE的长.
19. 如图,现有一块三角形的空地,其三条边长分别是20 m,30 m,40 m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.(要求:尺规作图,保留作图痕迹,不写作法)
20. 数学家鲁弗斯设计了一个仪器,它可以三等分一个角.如图所示,A,B,C,D分别固定在以O为公共端点的四根木条上,且OA=OB=OC=OD,E,F可以在中间的两根木条上滑动,AE=CE=BF=DF.
求证:∠AOE=∠EOF=∠FOD.
21. 如图,A,B两点分别在射线OM,ON上,点C在∠MON的内部且CA=CB,CD⊥OM,CE⊥ON,垂足分别为D,E,且AD=BE.
(1)求证:OC平分∠MON;
(2)如果AO=10,BO=4,求OD的长.
人教版 八年级数学 12.3 角平分线的性质 课时训练-答案
一、选择题
1. 【答案】A
2. 【答案】A [解析] 如图,过点P作PE⊥OA于点E.
∵OC平分∠AOB,PD⊥OB,∴PE=PD=3.
∵动点Q在射线OA上运动,∴PQ≥3.
∴线段PQ的长度不可能是2.
3. 【答案】A [解析] 如图,过点D作DE⊥AB于点E.
∵点D的坐标是(0,-3),
∴OD=3.
∵AD是△OAB的角平分线,
∴ED=OD=3,
即点D到AB的距离是3.
4. 【答案】C [解析] 作PM⊥OB于点M.∵OP平分∠AOB,PE⊥OA,PM⊥OB,∴PM=PE=3.∴PN≥3.
5. 【答案】C
【解析】如图,过点D作于E,
∵,,∴,
∵,BD平分,∴,即点D到AB的距离为2,故选C.
6. 【答案】C
【解析】由作图步骤可得:是的角平分线,∴∠COE=∠DOE,
∵OC=OD,OE=OE,OM=OM,
∴△COE≌△DOE,∴∠CEO=∠DEO,
∵∠COE=∠DOE,OC=OD,∴CM=DM,OM⊥CD,
∴S四边形OCED=S△COE+S△DOE=,
但不能得出,
∴A、B、D选项正确,不符合题意,C选项错误,符合题意,故选C.
7. 【答案】A [解析] 如图,到三条直线a,b,c的距离相等的点一共有4个.
8. 【答案】B [解析] 如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.
∵AF平分∠BAC,FZ⊥AE,FW⊥AB,
∴FZ=FW.同理FW=FY.
∴FZ=FY.
又∵FZ⊥AE,FY⊥CB,
∴∠FCZ=∠FCY.
由∠AFB=40°,易得∠ACB=80°.
∴∠ZCY=100°.∴∠BCF=50°.
二、填空题
9. 【答案】3 【解析】如解图,过点P作PD⊥OA于点D,∵OP为∠AOB的平分线,PC⊥OB于点C,∴PD=PC,∵PC=3,∴PD=3,即点P到点OA的距离为3.
10. 【答案】150 [解析] ∵DB⊥AE于点B,DC⊥AF于点C,且DB=DC,
∴AD是∠BAC的平分线.
∵∠BAC=40°,∴∠CAD=∠BAC=20°.
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
11. 【答案】∠AOP=∠BOP,PC⊥OA于点C,PD⊥OB于点D
12. 【答案】2.5 [解析] 设点O到AB,BC,AC的距离均为h,∴S△ABC=×8·h=10,解得h=2.5,即点O到AB的距离为2.5.
13. 【答案】65°
14. 【答案】12 [解析] 如图,连接BE.∵D为Rt△ABC中斜边BC上的一点,过点D作BC的垂线,交AC于点E,∴∠A=∠BDE=90°.
在Rt△DBE和Rt△ABE中,
∴Rt△DBE≌Rt△ABE(HL).∴DE=AE.∵AE=12 cm,∴DE=12 cm.
15. 【答案】90° [解析] ∵点P到AB,BD,CD的距离相等,∴BP,DP分别平分∠ABD,∠BDC.
∵AB∥CD,∴∠ABD+∠BDC=180°.
∴∠PBD+∠PDB=90°.故∠BPD=90°.
16. 【答案】32° [解析] ∵PD=PE=PF,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,
∴CP平分∠ACF,BP平分∠ABC.
∴∠PCF=∠ACF,∠PBF=∠ABC.
∴∠BPC=∠PCF-∠PBF=(∠ACF-∠ABC)=∠BAC=32°.
三、解答题
17. 【答案】
解:如图,过点D作DE⊥AB于点E,DF⊥AC于点F.
∵AD是∠BAC的平分线,∴DE=DF.
∵AB=20 m,AC=10 m,
∴S△ABC=×20×10=×20·DE+×10·DF,解得DE=(m).
∴△ACD的面积=×10×=(m2),
△ABD的面积=×20×=(m2).
故一串红的种植面积为 m2,鸡冠花的种植面积为 m2.
18. 【答案】
解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF.
设DE=x cm,则S△ABD=AB·DE=×20x=10x(cm2),S△ACD=AC·DF=×18x=9x(cm2).
∵S△ABC=S△ABD+S△ACD,∴10x+9x=142.5,
解得x=7.5,∴DE=7.5 cm.
19. 【答案】
解:(答案不唯一)如图,分别作∠ACB和∠ABC的平分线,相交于点P,连接PA,则△PAB,△PAC,△PBC的面积之比为2∶3∶4.
理由如下:
如图,过点P分别作PE⊥AB于点E,PF⊥AC于点F,PH⊥BC于点H.
∵P是∠ABC和∠ACB的平分线的交点,
∴PE=PF=PH.
∵S△PAB=AB·PE=10PE,S△PAC=AC·PF=15PF,S△PBC=BC·PH=20PH,
∴S△PAB∶S△PAC∶S△PBC=10∶15∶20=2∶3∶4.
20. 【答案】
证明:在△AOE和△COE中,
∴△AOE≌△COE(SSS).
∴∠AOE=∠COE.
同理∠COE=∠FOD.
∴∠AOE=∠EOF=∠FOD.
21. 【答案】
解:(1)证明:∵CD⊥OM,CE⊥ON,
∴∠CDA=∠CEB=90°.
在Rt△ACD与Rt△BCE中,
∴Rt△ACD≌Rt△BCE(HL).
∴CD=CE.
又∵CD⊥OM,CE⊥ON,∴OC平分∠MON.
(2)在Rt△ODC与Rt△OEC中,
∴Rt△ODC≌Rt△OEC.
∴OD=OE.
设BE=x.
∵BO=4,∴OE=OD=4+x.
∵AD=BE=x,
∴AO=OD+AD=4+2x=10.
∴x=3.∴OD=4+3=7.
一、选择题
1. 用直尺和圆规作一个角的平分线,示意图如图,则能说明OC是∠AOB的平分线的依据是( )
A.SSS B.SAS C.AAS D.ASA
2. 如图,OC平分∠AOB,P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是( )
A.2 B.3 C.4 D.5
3. 如图,在直角坐标系中,AD是Rt△OAB的角平分线,点D的坐标是(0,-3),那么点D到AB的距离是 ( )
A.3 B.-3 C.2 D.-2
4. 如图,OP平分∠AOB,点P到OA的距离为3,N是OB上的任意一点,则线段PN的长度的取值范围为 ( )
A.PN<3 B.PN>3 C.PN≥3 D.PN≤3
5. (2019?张家界)如图,在中,,,,BD平分,则点D到AB的距离等于
A.4 B.3 C.2 D.1
6. 如图,已知.按照以下步骤作图:①以点为圆心,以适当的长为半径作弧,分别交的两边于,两点,连接;②分别以点,为圆心,以大于线段的长为半径作弧,两弧在内交于点,连接,;③连接交于点.下列结论中错误的是
A. B.
C. D.
7. 如图,平面上到两两相交的三条直线a,b,c的距离相等的点一共有( )
A.4个 B.3个 C.2个 D.1个
8. 如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于点H.若∠AFB=40°,则∠BCF的度数为( )
A.40° B.50° C.55° D.60°
二、填空题
9. 如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为________.
10. 如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=________°.
11. 如图,请用符号语言表示“角的平分线上的点到角的两边的距离相等”.
条件:____________________________________.
结论:PC=PD.
12. △ABC的周长为8,面积为10,若其内部一点O到三边的距离相等,则点O到AB的距离为________.
13. 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为________.
14. 如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12 cm,则DE的长为 cm.?
15. 如图,AB∥CD,点P到AB,BD,CD的距离相等,则∠BPD的度数为________.
16. 如图,P是△ABC外的一点,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,连接PB,PC.若PD=PE=PF,∠BAC=64°,则∠BPC的度数为________.
三、解答题
17. 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20 m,AC=10 m,分别求一串红与鸡冠花两种花草的种植面积.
18. 如图,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是142.5 cm2,AB=20 cm,AC=18 cm,求DE的长.
19. 如图,现有一块三角形的空地,其三条边长分别是20 m,30 m,40 m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.(要求:尺规作图,保留作图痕迹,不写作法)
20. 数学家鲁弗斯设计了一个仪器,它可以三等分一个角.如图所示,A,B,C,D分别固定在以O为公共端点的四根木条上,且OA=OB=OC=OD,E,F可以在中间的两根木条上滑动,AE=CE=BF=DF.
求证:∠AOE=∠EOF=∠FOD.
21. 如图,A,B两点分别在射线OM,ON上,点C在∠MON的内部且CA=CB,CD⊥OM,CE⊥ON,垂足分别为D,E,且AD=BE.
(1)求证:OC平分∠MON;
(2)如果AO=10,BO=4,求OD的长.
人教版 八年级数学 12.3 角平分线的性质 课时训练-答案
一、选择题
1. 【答案】A
2. 【答案】A [解析] 如图,过点P作PE⊥OA于点E.
∵OC平分∠AOB,PD⊥OB,∴PE=PD=3.
∵动点Q在射线OA上运动,∴PQ≥3.
∴线段PQ的长度不可能是2.
3. 【答案】A [解析] 如图,过点D作DE⊥AB于点E.
∵点D的坐标是(0,-3),
∴OD=3.
∵AD是△OAB的角平分线,
∴ED=OD=3,
即点D到AB的距离是3.
4. 【答案】C [解析] 作PM⊥OB于点M.∵OP平分∠AOB,PE⊥OA,PM⊥OB,∴PM=PE=3.∴PN≥3.
5. 【答案】C
【解析】如图,过点D作于E,
∵,,∴,
∵,BD平分,∴,即点D到AB的距离为2,故选C.
6. 【答案】C
【解析】由作图步骤可得:是的角平分线,∴∠COE=∠DOE,
∵OC=OD,OE=OE,OM=OM,
∴△COE≌△DOE,∴∠CEO=∠DEO,
∵∠COE=∠DOE,OC=OD,∴CM=DM,OM⊥CD,
∴S四边形OCED=S△COE+S△DOE=,
但不能得出,
∴A、B、D选项正确,不符合题意,C选项错误,符合题意,故选C.
7. 【答案】A [解析] 如图,到三条直线a,b,c的距离相等的点一共有4个.
8. 【答案】B [解析] 如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.
∵AF平分∠BAC,FZ⊥AE,FW⊥AB,
∴FZ=FW.同理FW=FY.
∴FZ=FY.
又∵FZ⊥AE,FY⊥CB,
∴∠FCZ=∠FCY.
由∠AFB=40°,易得∠ACB=80°.
∴∠ZCY=100°.∴∠BCF=50°.
二、填空题
9. 【答案】3 【解析】如解图,过点P作PD⊥OA于点D,∵OP为∠AOB的平分线,PC⊥OB于点C,∴PD=PC,∵PC=3,∴PD=3,即点P到点OA的距离为3.
10. 【答案】150 [解析] ∵DB⊥AE于点B,DC⊥AF于点C,且DB=DC,
∴AD是∠BAC的平分线.
∵∠BAC=40°,∴∠CAD=∠BAC=20°.
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
11. 【答案】∠AOP=∠BOP,PC⊥OA于点C,PD⊥OB于点D
12. 【答案】2.5 [解析] 设点O到AB,BC,AC的距离均为h,∴S△ABC=×8·h=10,解得h=2.5,即点O到AB的距离为2.5.
13. 【答案】65°
14. 【答案】12 [解析] 如图,连接BE.∵D为Rt△ABC中斜边BC上的一点,过点D作BC的垂线,交AC于点E,∴∠A=∠BDE=90°.
在Rt△DBE和Rt△ABE中,
∴Rt△DBE≌Rt△ABE(HL).∴DE=AE.∵AE=12 cm,∴DE=12 cm.
15. 【答案】90° [解析] ∵点P到AB,BD,CD的距离相等,∴BP,DP分别平分∠ABD,∠BDC.
∵AB∥CD,∴∠ABD+∠BDC=180°.
∴∠PBD+∠PDB=90°.故∠BPD=90°.
16. 【答案】32° [解析] ∵PD=PE=PF,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,
∴CP平分∠ACF,BP平分∠ABC.
∴∠PCF=∠ACF,∠PBF=∠ABC.
∴∠BPC=∠PCF-∠PBF=(∠ACF-∠ABC)=∠BAC=32°.
三、解答题
17. 【答案】
解:如图,过点D作DE⊥AB于点E,DF⊥AC于点F.
∵AD是∠BAC的平分线,∴DE=DF.
∵AB=20 m,AC=10 m,
∴S△ABC=×20×10=×20·DE+×10·DF,解得DE=(m).
∴△ACD的面积=×10×=(m2),
△ABD的面积=×20×=(m2).
故一串红的种植面积为 m2,鸡冠花的种植面积为 m2.
18. 【答案】
解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF.
设DE=x cm,则S△ABD=AB·DE=×20x=10x(cm2),S△ACD=AC·DF=×18x=9x(cm2).
∵S△ABC=S△ABD+S△ACD,∴10x+9x=142.5,
解得x=7.5,∴DE=7.5 cm.
19. 【答案】
解:(答案不唯一)如图,分别作∠ACB和∠ABC的平分线,相交于点P,连接PA,则△PAB,△PAC,△PBC的面积之比为2∶3∶4.
理由如下:
如图,过点P分别作PE⊥AB于点E,PF⊥AC于点F,PH⊥BC于点H.
∵P是∠ABC和∠ACB的平分线的交点,
∴PE=PF=PH.
∵S△PAB=AB·PE=10PE,S△PAC=AC·PF=15PF,S△PBC=BC·PH=20PH,
∴S△PAB∶S△PAC∶S△PBC=10∶15∶20=2∶3∶4.
20. 【答案】
证明:在△AOE和△COE中,
∴△AOE≌△COE(SSS).
∴∠AOE=∠COE.
同理∠COE=∠FOD.
∴∠AOE=∠EOF=∠FOD.
21. 【答案】
解:(1)证明:∵CD⊥OM,CE⊥ON,
∴∠CDA=∠CEB=90°.
在Rt△ACD与Rt△BCE中,
∴Rt△ACD≌Rt△BCE(HL).
∴CD=CE.
又∵CD⊥OM,CE⊥ON,∴OC平分∠MON.
(2)在Rt△ODC与Rt△OEC中,
∴Rt△ODC≌Rt△OEC.
∴OD=OE.
设BE=x.
∵BO=4,∴OE=OD=4+x.
∵AD=BE=x,
∴AO=OD+AD=4+2x=10.
∴x=3.∴OD=4+3=7.
