人教版 九年级数学 上册第25章 概率初步 单元训练(word含答案)
文档属性
| 名称 | 人教版 九年级数学 上册第25章 概率初步 单元训练(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 12:54:07 | ||
图片预览



文档简介
人教版 九年级数学 第25章 概率初步 课时训练
一、选择题
1. 从正五边形的五个顶点中,任取四个顶点连成四边形,对于事件M:“这个四边形是等腰梯形”,下列推断正确的是( )
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为 D. 事件M发生的概率为
2. 2019·泰州 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表:
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20 B.300 C.500 D.800
3. 下列说法错误的是( )
A.必然事件发生的概率是1
B.通过大量重复试验,可以用频率估计概率
C.概率很小的事件不可能发生
D.投一枚图钉,“钉尖朝上”的概率不能用列举法求得
4. 下列说法正确的是( )
A.可能性很小的事件在一次试验中一定不会发生
B.可能性很小的事件在一次试验中一定发生
C.可能性很小的事件在一次试验中有可能发生
D.不可能事件在一次试验中也可能发生
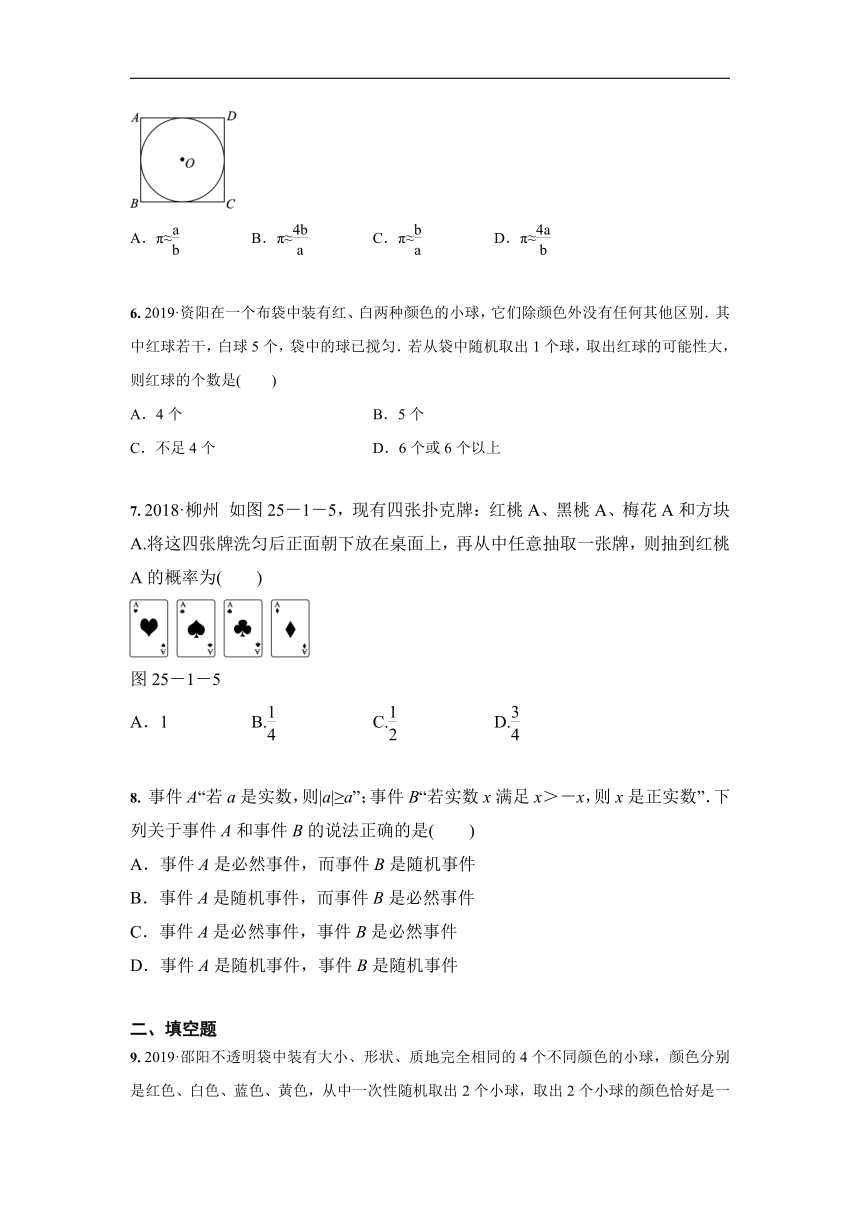
5. 如图,正方形ABCD内有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数为a,⊙O内的点数为b(在正方形边上和圆上的点不在统计中).根据用频率估计概率的原理,可推得π的大小是 ( )
A.π≈ B.π≈ C.π≈ D.π≈
6. 2019·资阳在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是( )
A.4个 B.5个
C.不足4个 D.6个或6个以上
7. 2018·柳州 如图25-1-5,现有四张扑克牌:红桃A、黑桃A、梅花A和方块A.将这四张牌洗匀后正面朝下放在桌面上,再从中任意抽取一张牌,则抽到红桃A的概率为( )
图25-1-5
A.1 B. C. D.
8. 事件A“若a是实数,则|a|≥a”;事件B“若实数x满足x>-x,则x是正实数”.下列关于事件A和事件B的说法正确的是( )
A.事件A是必然事件,而事件B是随机事件
B.事件A是随机事件,而事件B是必然事件
C.事件A是必然事件,事件B是必然事件
D.事件A是随机事件,事件B是随机事件
二、填空题
9. 2019·邵阳不透明袋中装有大小、形状、质地完全相同的4个不同颜色的小球,颜色分别是红色、白色、蓝色、黄色,从中一次性随机取出2个小球,取出2个小球的颜色恰好是一红一蓝的概率是________.
10. 某市初中毕业男生体育测试项目有四项,其中“立定跳远”“1000米跑”“肺活量测试”为必测项目,另外从“引体向上”“推铅球”中选一项进行测试.小亮、小明和小刚从“引体向上”“推铅球”中选择同一个测试项目的概率是________.
11. 2019·贵阳 一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出1个球,如果摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是____________.
12. 从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色不同外,其他都一样,由此估计口袋中有________个白球.
13. 一枚质地均匀的骰子的6个面上分别刻有1~6的点数,抛掷这枚骰子一次,向上一面的点数是4的概率是________.
14. 如图,转盘中6个扇形的面积相等,任意转动转盘1次,转盘停止转动后,指针指向的数小于5的概率为________.
15. 点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是________.
16. 已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则能使电路形成通路的概率是________.
三、解答题
17. 某路口红绿灯的时间设置为红灯40秒,绿灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到哪一种灯的可能性最大?遇到哪一种灯的可能性最小?根据是什么?
18. 只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润从哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是:“每个大于2的偶数都可以表示为两个素数的和.”如20=3+17.
(1)若从7,11,19,23这4个素数中随机抽取一个,则抽到的数是7的概率是________;
(2)从7,11,19,23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,再用画树状图或列表的方法,求抽到的2个素数之和等于30的概率.
19. “共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图41-K-2是四位院士(依次记为A,B,C,D),为了让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可以从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报.求小明和小华查找同一位院士资料的概率.
20. 在甲、乙两个不透明的口袋中装有大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字1,2,3,4,乙袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中任意摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)的可能的结果;
(2)若m,n都是方程x2-5x+6=0的解,则小明获胜;若m,n都不是方程x2-5x+6=0的解,则小利获胜,他们两人谁获胜的概率大?
21. 方案设计盒中装有红球、黄球共10个,每个球除颜色不同外其余都相同,每次从盒中摸出1个球,摸三次,不放回,请你按要求设计盒中红球的个数.
(1)“摸出的3个球都是红球”是不可能事件;
(2)“摸出红球”是必然事件;
(3)“至少摸出2个黄球”是确定性事件;
(4)“至少摸出2个黄球”是随机事件.
人教版 九年级数学 第25章 概率初步 课时训练-答案
一、选择题
1. 【答案】B 【解析】本题考查正多边形的性质、等腰梯形的判定以及概率的相关概念. 解题思路:先证明出符合条件的四边形是等腰梯形.所以事件M是必然事件.故选B.
2. 【答案】C
3. 【答案】C
4. 【答案】C
5. 【答案】B [解析] 设圆的半径为r,则正方形的边长为2r.根据题意,得≈,故π≈.故选B.
6. 【答案】D [解析] 因为袋子中白球有5个,且从袋中随机取出1个球,取出红球的可能性大,
所以红球的个数比白球个数多,
所以红球个数为6个或6个以上.故选D.
7. 【答案】B
8. 【答案】C [解析] 当a是非负实数时,有|a|=a,当a是负实数时,有|a|>a,∴事件A是必然事件;“若实数x满足x>-x,则x是正实数”也是一个必然事件.
二、填空题
9. 【答案】 [解析] 画树状图如下:
由树状图知,共有12种等可能的结果,其中取出2个小球的颜色恰好是一红一蓝的结果有2种,
所以取出2个小球的颜色恰好是一红一蓝的概率为=.故答案为.
10. 【答案】 [解析] 分别用A,B代表“引体向上”与“推铅球”,画树状图如图所示.由图可知共有8种等可能的结果,小亮、小明和小刚从“引体向上”“推铅球”中选择同一个测试项目的有2种结果,所以小亮、小明和小刚从“引体向上”“推铅球”中选择同一个测试项目的概率是=.
11. 【答案】m+n=10 [解析] ∵一个袋中装有m个红球,10个黄球,n个白球,摸到黄球的概率与不是黄球的概率相同,∴m与n的关系是m+n=10.
故答案为m+n=10.
12. 【答案】20 [解析] 摸了150次,其中有50次摸到黑球,则摸到黑球的频率是=.
设口袋中有x个白球,则=,
解得x=20.
经检验,x=20是原方程的解,
故答案为20.
13. 【答案】 [解析] 抛掷骰子一次,向上一面的点数可能是1,2,3,4,5,6,一共有6种等可能的结果,其中向上一面的点数是4的结果有1种,所以P(向上一面的点数是4)=.
14. 【答案】 [解析] 转盘转动一次,出现6种等可能的结果,小于5的结果共有4种,故指针指向的数小于5的概率为=.
15. 【答案】 [解析] 画树状图如下:
共有20种等可能的结果,其中点P(a,b)在平面直角坐标系中第二象限内的结果有4种,
所以点P(a,b)在平面直角坐标系中第二象限内的概率为=.
16. 【答案】 [解析] 列表如下:
∴一共有20种等可能的结果,使电路形成通路的结果有12种,
∴使电路形成通路的概率是=.
三、解答题
17. 【答案】
解:当人或车随意经过该路口时,遇到绿灯的可能性最大,遇到黄灯的可能性最小.根据:绿灯持续的时间最长,黄灯持续的时间最短.
18. 【答案】
解:(1)从7,11,19,23这4个素数中随机抽取一个,抽到的数是7的概率是.故答案为.
(2)画树状图如图所示:
共有12种等可能的结果,其中满足条件的结果有4种,所以抽到的2个素数之和等于30的概率为=.
19. 【答案】
解:根据题意画树状图如下:
共有16种等可能的结果,其中小明和小华查找同一位院士资料的结果有4种,所以小明和小华查找同一位院士资料的概率为=.
20. 【答案】
解:(1)画树状图如图所示:
(2)因为解方程x2-5x+6=0,得x=2或x=3.
由树状图得共有12种等可能的结果,其中m,n都是方程x2-5x+6=0的解的结果有4种,
m,n都不是方程x2-5x+6=0的解的结果有2种,
所以小明获胜的概率为=,小利获胜的概率为=,
所以小明获胜的概率大.
21. 【答案】
解:(1)2个或1个.
(2)8个或9个.
(3)9个或1个.
(4)多于1个且小于9个.
一、选择题
1. 从正五边形的五个顶点中,任取四个顶点连成四边形,对于事件M:“这个四边形是等腰梯形”,下列推断正确的是( )
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为 D. 事件M发生的概率为
2. 2019·泰州 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表:
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20 B.300 C.500 D.800
3. 下列说法错误的是( )
A.必然事件发生的概率是1
B.通过大量重复试验,可以用频率估计概率
C.概率很小的事件不可能发生
D.投一枚图钉,“钉尖朝上”的概率不能用列举法求得
4. 下列说法正确的是( )
A.可能性很小的事件在一次试验中一定不会发生
B.可能性很小的事件在一次试验中一定发生
C.可能性很小的事件在一次试验中有可能发生
D.不可能事件在一次试验中也可能发生
5. 如图,正方形ABCD内有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数为a,⊙O内的点数为b(在正方形边上和圆上的点不在统计中).根据用频率估计概率的原理,可推得π的大小是 ( )
A.π≈ B.π≈ C.π≈ D.π≈
6. 2019·资阳在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是( )
A.4个 B.5个
C.不足4个 D.6个或6个以上
7. 2018·柳州 如图25-1-5,现有四张扑克牌:红桃A、黑桃A、梅花A和方块A.将这四张牌洗匀后正面朝下放在桌面上,再从中任意抽取一张牌,则抽到红桃A的概率为( )
图25-1-5
A.1 B. C. D.
8. 事件A“若a是实数,则|a|≥a”;事件B“若实数x满足x>-x,则x是正实数”.下列关于事件A和事件B的说法正确的是( )
A.事件A是必然事件,而事件B是随机事件
B.事件A是随机事件,而事件B是必然事件
C.事件A是必然事件,事件B是必然事件
D.事件A是随机事件,事件B是随机事件
二、填空题
9. 2019·邵阳不透明袋中装有大小、形状、质地完全相同的4个不同颜色的小球,颜色分别是红色、白色、蓝色、黄色,从中一次性随机取出2个小球,取出2个小球的颜色恰好是一红一蓝的概率是________.
10. 某市初中毕业男生体育测试项目有四项,其中“立定跳远”“1000米跑”“肺活量测试”为必测项目,另外从“引体向上”“推铅球”中选一项进行测试.小亮、小明和小刚从“引体向上”“推铅球”中选择同一个测试项目的概率是________.
11. 2019·贵阳 一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出1个球,如果摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是____________.
12. 从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色不同外,其他都一样,由此估计口袋中有________个白球.
13. 一枚质地均匀的骰子的6个面上分别刻有1~6的点数,抛掷这枚骰子一次,向上一面的点数是4的概率是________.
14. 如图,转盘中6个扇形的面积相等,任意转动转盘1次,转盘停止转动后,指针指向的数小于5的概率为________.
15. 点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是________.
16. 已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则能使电路形成通路的概率是________.
三、解答题
17. 某路口红绿灯的时间设置为红灯40秒,绿灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到哪一种灯的可能性最大?遇到哪一种灯的可能性最小?根据是什么?
18. 只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润从哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是:“每个大于2的偶数都可以表示为两个素数的和.”如20=3+17.
(1)若从7,11,19,23这4个素数中随机抽取一个,则抽到的数是7的概率是________;
(2)从7,11,19,23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,再用画树状图或列表的方法,求抽到的2个素数之和等于30的概率.
19. “共和国勋章”是中华人民共和国的最高荣誉勋章,在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图41-K-2是四位院士(依次记为A,B,C,D),为了让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可以从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应院士的资料制作小报.求小明和小华查找同一位院士资料的概率.
20. 在甲、乙两个不透明的口袋中装有大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字1,2,3,4,乙袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中任意摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)的可能的结果;
(2)若m,n都是方程x2-5x+6=0的解,则小明获胜;若m,n都不是方程x2-5x+6=0的解,则小利获胜,他们两人谁获胜的概率大?
21. 方案设计盒中装有红球、黄球共10个,每个球除颜色不同外其余都相同,每次从盒中摸出1个球,摸三次,不放回,请你按要求设计盒中红球的个数.
(1)“摸出的3个球都是红球”是不可能事件;
(2)“摸出红球”是必然事件;
(3)“至少摸出2个黄球”是确定性事件;
(4)“至少摸出2个黄球”是随机事件.
人教版 九年级数学 第25章 概率初步 课时训练-答案
一、选择题
1. 【答案】B 【解析】本题考查正多边形的性质、等腰梯形的判定以及概率的相关概念. 解题思路:先证明出符合条件的四边形是等腰梯形.所以事件M是必然事件.故选B.
2. 【答案】C
3. 【答案】C
4. 【答案】C
5. 【答案】B [解析] 设圆的半径为r,则正方形的边长为2r.根据题意,得≈,故π≈.故选B.
6. 【答案】D [解析] 因为袋子中白球有5个,且从袋中随机取出1个球,取出红球的可能性大,
所以红球的个数比白球个数多,
所以红球个数为6个或6个以上.故选D.
7. 【答案】B
8. 【答案】C [解析] 当a是非负实数时,有|a|=a,当a是负实数时,有|a|>a,∴事件A是必然事件;“若实数x满足x>-x,则x是正实数”也是一个必然事件.
二、填空题
9. 【答案】 [解析] 画树状图如下:
由树状图知,共有12种等可能的结果,其中取出2个小球的颜色恰好是一红一蓝的结果有2种,
所以取出2个小球的颜色恰好是一红一蓝的概率为=.故答案为.
10. 【答案】 [解析] 分别用A,B代表“引体向上”与“推铅球”,画树状图如图所示.由图可知共有8种等可能的结果,小亮、小明和小刚从“引体向上”“推铅球”中选择同一个测试项目的有2种结果,所以小亮、小明和小刚从“引体向上”“推铅球”中选择同一个测试项目的概率是=.
11. 【答案】m+n=10 [解析] ∵一个袋中装有m个红球,10个黄球,n个白球,摸到黄球的概率与不是黄球的概率相同,∴m与n的关系是m+n=10.
故答案为m+n=10.
12. 【答案】20 [解析] 摸了150次,其中有50次摸到黑球,则摸到黑球的频率是=.
设口袋中有x个白球,则=,
解得x=20.
经检验,x=20是原方程的解,
故答案为20.
13. 【答案】 [解析] 抛掷骰子一次,向上一面的点数可能是1,2,3,4,5,6,一共有6种等可能的结果,其中向上一面的点数是4的结果有1种,所以P(向上一面的点数是4)=.
14. 【答案】 [解析] 转盘转动一次,出现6种等可能的结果,小于5的结果共有4种,故指针指向的数小于5的概率为=.
15. 【答案】 [解析] 画树状图如下:
共有20种等可能的结果,其中点P(a,b)在平面直角坐标系中第二象限内的结果有4种,
所以点P(a,b)在平面直角坐标系中第二象限内的概率为=.
16. 【答案】 [解析] 列表如下:
∴一共有20种等可能的结果,使电路形成通路的结果有12种,
∴使电路形成通路的概率是=.
三、解答题
17. 【答案】
解:当人或车随意经过该路口时,遇到绿灯的可能性最大,遇到黄灯的可能性最小.根据:绿灯持续的时间最长,黄灯持续的时间最短.
18. 【答案】
解:(1)从7,11,19,23这4个素数中随机抽取一个,抽到的数是7的概率是.故答案为.
(2)画树状图如图所示:
共有12种等可能的结果,其中满足条件的结果有4种,所以抽到的2个素数之和等于30的概率为=.
19. 【答案】
解:根据题意画树状图如下:
共有16种等可能的结果,其中小明和小华查找同一位院士资料的结果有4种,所以小明和小华查找同一位院士资料的概率为=.
20. 【答案】
解:(1)画树状图如图所示:
(2)因为解方程x2-5x+6=0,得x=2或x=3.
由树状图得共有12种等可能的结果,其中m,n都是方程x2-5x+6=0的解的结果有4种,
m,n都不是方程x2-5x+6=0的解的结果有2种,
所以小明获胜的概率为=,小利获胜的概率为=,
所以小明获胜的概率大.
21. 【答案】
解:(1)2个或1个.
(2)8个或9个.
(3)9个或1个.
(4)多于1个且小于9个.
同课章节目录
