苏科版九年级数学下册 5.3 用待定系数法确定二次函数的表达式二次函数 同步测试题(Word版 有答案)
文档属性
| 名称 | 苏科版九年级数学下册 5.3 用待定系数法确定二次函数的表达式二次函数 同步测试题(Word版 有答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 65.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 13:15:32 | ||
图片预览
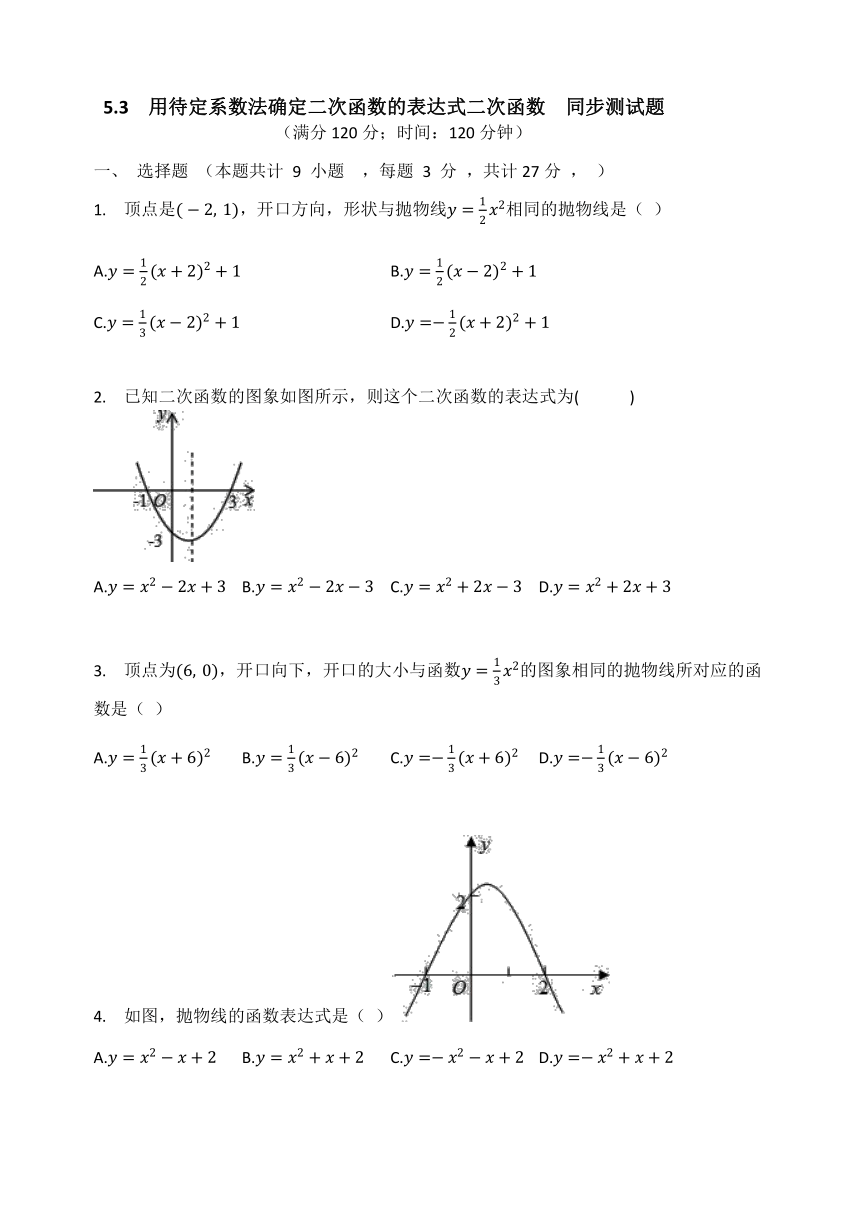




文档简介
10858500119380001231900005.3 用待定系数法确定二次函数的表达式二次函数 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
1. 顶点是(-2,?1),开口方向,形状与抛物线y=12x2相同的抛物线是( )
A.y=12(x+2)2+1 B.y=12(x-2)2+1
C.y=13(x-2)2+1 D.y=-12(x+2)2+1
?
2. 已知二次函数的图象如图所示,则这个二次函数的表达式为(? ? ? ? )
A.y=x2-2x+3 B.y=x2-2x-3 C.y=x2+2x-3 D.y=x2+2x+3
?
3. 顶点为(6,?0),开口向下,开口的大小与函数y=13x2的图象相同的抛物线所对应的函数是( )
A.y=13(x+6)2 B.y=13(x-6)2 C.y=-13(x+6)2 D.y=-13(x-6)2
?
4. 如图,抛物线的函数表达式是( )
A.y=x2-x+2 B.y=x2+x+2 C.y=-x2-x+2 D.y=-x2+x+2
?
5. 下表是变量x与y的一组对应值:
x
-2
-1
0
1
2
3
y
1
-0.5
-1
-0.5
1
3.5
从这组数据看,y与x的函数关系是( )
A.正比例函数 B.常数项不为零的一次函数
C.二次函数 D.反比例函数
?6. 抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
A.y=x2-x-2 B.y=-12x2-12x+2
C.y=-12x2-12x+1 D.y=-x2+x+2
?
7. 一个二次函数,当x=0时,y=-5;当x=-1时,y=-4;当x=-2时,y=5,则这个二次函数的关系式是( )
A.y=4x2+3x-5 B.y=2x2+x+5 C.y=2x2-x+5 D.y=2x2+x-5
?
8. 若所求的二次函数图象与抛物线y=2x2-4x-1有相同的顶点,并且在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,则所求二次函数的解析式为(? ? ? ? )
A.y=-x2+2x+4 B.y=-ax2-2ax-3(a>0)
C.y=-2x2-4x-5 D.y=ax2-2ax+a-3(a<0)
?
9. 若a,b,c满足a+b+c=0,a-b+c=0,则关于x的方程ax2+bx+c=0a≠0的解是(? ? ? ? )
A.1,0 B.-1,0 C.1,-1 D.无法确定
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
10. 已知:二次函数的图象过A(1,?0),B(k,?0),C(0,?k)(k≠1).若D是抛物线的顶点,且△ABD是直角三角形,则k=________.
?
11. 二次函数y=x2-2mx+m2-1经过原点,则此二次函数的解析式为________.
?
12. 已知抛物线y=ax2+bx+c与x轴交于A(-2,?0),B(4,?0)两点,顶点C到x轴的距离为2,则此抛物线的解析式为________.
?
13. 若抛物线y=ax2+bx+c的顶点是A(2,?1),且经过点B(1,?0),则抛物线的函数关系式为________.
?
14. 已知直线 y=x+1 与抛物线 y=ax2+2x+c 相交于点 A(-1,0) 和点 B(2,m)两点.则该抛物线的函数表达式是________.
?
15. 二次函数y=ax2+bx+c的图象经过点(-1,?0),(3,?0),(0,?2),当x=2时,y的值为________.
?
16. 二次函数y=ax2+bx+c经过三个点A(-3,?0)、B(0,?3)、C(2,?-5),则二次函数解析式为________.
?
17. 二次函数的图象经过原点(-1,?-2),且图象与x轴的另一交点到原点的距离为2.则二次函数的解析式为________.
?
18. 如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为________.
三、 解答题 (本题共计 8 小题,共66分 , ) ?
19. 已知二次函数y=ax2+bx+c的图象经过A(-1,?0),B(3,?0),C(0,?-3)三点,求这个二次函数的解析式.
?
20. 根据所给条件求抛物线的解析式:
(1)抛物线过点(0,?2)、(1,?1)、(3,?5);
(2)抛物线关于y轴对称,且过点(1,?-2)和(-2,?0).
?
21. 已知二次函数y=ax2+2x+c的图象经过点(-2,?-5),(1,?4).求这个二次函数的解析式.
?
22. 已知二次函数图像的顶点坐标为(1,?-3),且过点(2,?0),求这个二次函数的解析式.
?
23. 已知一个二次函数的图象经过点(1,?-1),(0,?-1),(-1,?13),求这个二次函数的解析式.
?
24. 已知二次函数y=ax2-4ax+b的图象经过点A(1,?0),B(x2,?0),与y轴正半轴交于C点,且S△ABC=2,
求二次函数的解析式.
?
25. 已知抛物线y=ax2+bx+c经过(-1,?0),(0,?-3),(2,?3)三点.
(1)求这条抛物线的表达式.
(2)写出抛物线的开口方向、对称轴和顶点坐标.
?
26. 有一个二次函数的图象,三位学生分别说出了它的一些特点.
甲:对称轴是直线x=4;
乙:与x轴两交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3;
请写出满足上述全部特点的二次函数解析式.
参考答案
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
1.
【答案】
A
【解答】
解:根据题意得:抛物线解析式为y=12(x+2)2+1,
故选A
2.
【答案】
B
【解答】
解:设二次函数的表达式为y=ax2+bx+c,
抛物线过(-1,?0),(0,?-3),(3,?0),
所以a-b+c=0c=-39a+3b+c=0,
解得a=1,b=-2,c=-3,
这个二次函数的表达式为y=x2-2x-3.
故选B.
3.
【答案】
D
【解答】
解:∵ 一个二次函数的图象开口向下,开口的大小与函数y=13x2的图象相同,
故设该二次函数的解析为y=-13(x-h)2+k,
∴ 该函数的顶点坐标为:(h,?k),
又∵ 该二次函数的顶点为(6,?0),
∴ h=6,k=0,
∴ 该二次函数的解析为y=-13(x-6)2.
故选D.
4.
【答案】
D
【解答】
解:根据题意,设二次函数的表达式为y=ax2+bx+c,
抛物线过(-1,?0),(0,?2),(2,?0),
所以a-b+c=0c=24a+2b+c=0,
解得a=-1,b=1,c=2,
这个二次函数的表达式为y=-x2+x+2.
故选D.
5.
【答案】
C
【解答】
解:观察可知,函数图象关于y轴对称,顶点坐标是(0,?-1),
∴ 设函数解析式为y=ax2-1,
当x=1时,a-1=-0.5,
解得a=12,
y=12x2-1,
所以是二次函数.
故选C.
6.
【答案】
D
【解答】
解:A、由图象可知开口向下,故a<0,此选项错误;
B、抛物线过点(-1,?0),(2,?0),根据抛物线的对称性,顶点的横坐标是12,
而y=-12x2-12x+2的顶点横坐标是--122×(-12)=-12,故此选项错误;
C、y=-12x2-12x+1的顶点横坐标是-12,故此选项错误;
D、y=-x2+x+2的顶点横坐标是12,并且抛物线过点(-1,?0),(2,?0),故此选项正确.
故选D.
7.
【答案】
A
【解答】
解:设二次函数的关系式是y=ax2+bx+c(a≠0),
∵ 当x=0时,y=-5;当x=-1时,y=-4;当x=-2时,y=5,
∴ c=-5①,
a-b+c=-4②,
4a-2b+c=5③,
解由①②③组成的方程组得,a=4,b=3,c=-5,
所以二次函数的关系式为:y=4x2+3x-5.
故选A.
8.
【答案】
D
【解答】
解:抛物线y=2x2-4x-1的顶点坐标为(1,?-3),
根据题意得所求的二次函数的解析式的顶点坐标是(1,?-3),
且抛物线开口向下.
A,抛物线开口向下,顶点坐标是(1,?5),故选项A错误;
B,抛物线开口向下,顶点坐标是(-1,?a-3),故选项B错误;
C,抛物线开口向下,顶点坐标是(-1,?-3),故选项C错误;
D,抛物线开口向下,顶点坐标是(1,?-3),故选项D正确.
故选D.
9.
【答案】
C
【解答】
解:a+b+c=0①,a-b+c=0②,
①-②得,2b=0,所以b=0.
①+②得,2a+2c=0,
所以a+c=0,即a=-c(c≠0).
把b=0代入关于x的方程ax2+bx+c=0得,ax2+c=0,
所以x2=-ca=1,
即x1=1?,?x2=-1.
故选C.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
10.
【答案】
-1或3
【解答】
解:根据题意设二次函数的解析式为y=ax2+bx+k,二次函数的图象过A(1,?0),B(k,?0),
则a+b+k=0ak2+bk+k=0,
解得a=1,b=-k-1;
二次函数的解析式为y=x2-(k+1)x+k,
当k>1时,函数的图象如图1,
对称轴DE为x=k+12,顶点坐标为(k+12,?-(k-1)24),
若△ABD是直角三角形,AD=DB,
则AE=DE,k+12-1=(k-1)24,
解得k=3,
当k<0,函数的图象如图2,
同理求出k=-1;
所以D是抛物线的顶点,且△ABD是直角三角形,则k=-1或3;
故答案为-1或3.
11.
【答案】
y=x2-2x或y=x2+2x
【解答】
解:把(0,?0)代入y=x2-2mx+m2-1得m2-1=0,解得m=1或m=-1,
当m=1时,二次函数的解析式为y=x2-2x;当m=-1时,二次函数的解析式为y=x2+2x,
即二次函数的解析式为y=x2-2x或y=x2+2x.
故答案为y=x2-2x或y=x2+2x.
12.
【答案】
y=-29x2+49x+169或y=29x2-49x-169
【解答】
解:∵ 抛物线y=ax2+bx+c与x轴交于A(-2,?0),B(4,?0)两点,
∴ 抛物线的对称轴为直线x=1,
∵ 顶点C到x轴的距离为2,
∴ C点坐标为(1,?2)或(1,?-2),
设抛物线解析式为y=a(x+2)(x-4),
把C(1,?2)代入得a×3×(-3)=2,解得a=-29,所以此时抛物线解析式为y=-29(x+2)(x-4)=-29x2+49x+169;
把C(1,?-2)代入得a×3×(-3)=-2,解得a=29,所以此时抛物线解析式为y=29(x+2)(x-4)=29x2-49x-169,
∴ 抛物线解析式为y=-29x2+49x+169或y=29x2-49x-169.
故答案为y=-29x2+49x+169或y=29x2-49x-169.
13.
【答案】
y=-x2+4x-3
【解答】
解:设抛物线的解析式为y=a(x-2)2+1,
将B(1,?0)代入y=a(x-2)2+1,
得a=-1,
函数解析式为y=-(x-2)2+1,
展开得y=-x2+4x-3.
故答案为:y=-x2+4x-3.
14.
【答案】
y=-x2+2x+3
【解答】
解:由题知:点B(2,m)在直线y=x+1上,
故m=2+1=3.
∴ 点B(2,3)和点A(-1,0)在抛物线上,
∴ a-2+c=0,4a+4+c=3,
由上述解得:a=-1,c=3,
故解析式为:y=-x2+2x+3.
故答案为:y=-x2+2x+3.
15.
【答案】
2
【解答】
解:如图所示,
∵ 二次函数y=ax2+bx+c的图象经过点(-1,?0),(3,?0)和(0,?2),
∴ a-b+c=0,9a+3b+c=0,c=2,?
解得:a=-23,b=43,c=2.?
则这个二次函数的表达式为y=-23x2+43x+2.
把x=2代入得,y=-23×4+43×2+2=2.
故答案为:2.
16.
【答案】
y=-x2-2x+3
【解答】
解:根据题意,得
9a-3b+c=0c=34a+2b+c=-5,
解得,a=-1b=-2c=3,
∴ 二次函数解析式为y=-x2-2x+3.
故答案是:y=-x2-2x+3.
17.
【答案】
y=2x2+4x或y=-23x2+43x
【解答】
解:根据题意得,与x轴的另一个交点为(2,?0)或(-2,?0),因此要分两种情况:
(1)过点(-2,?0),设y=ax(x+2),则-2=-a,解得:a=2,
∴ 抛物线的解析式为:y=2x2+4x;
(2)过点(2,?0),设y=ax(x-2),则-2=3a,解得:a=-23,
∴ 抛物线的解析式为:y=-23x2+43x.
故答案为y=2x2+4x或y=-23x2+43x.
18.
【答案】
(3-52,?3-52)
【解答】
A的坐标是(1,?0)、C坐标是(0,?1),设出解析式是y=a(x-1)2,把C的坐标代入得:a(-1)2=1,
解得:a=1,
则抛物线的解析式是:y=(x-1)2;
∵ B的坐标是(1,?1),
设OB解析式的解析式是y=kx,则k=1,则OB的解析式是y=x.
根据题意得:y=(x-1)2y=x?,
解得:x=3+52y=3+52?(舍去),或x=3-52y=3-52?.
则D的坐标是:(3-52,?3-52).
三、 解答题 (本题共计 8 小题 ,每题 10 分 ,共计80分 )
19.
【答案】
解:设抛物线的解析式为y=a(x+1)(x-3),
把C(0,?-3)代入得a×1×(-3)=-3,
解得a=1,
所以这个二次函数的解析式为y=(x+1)(x-3)=x2-2x-3.
【解答】
解:设抛物线的解析式为y=a(x+1)(x-3),
把C(0,?-3)代入得a×1×(-3)=-3,
解得a=1,
所以这个二次函数的解析式为y=(x+1)(x-3)=x2-2x-3.
20.
【答案】
解:(1)设抛物线解析式为y=ax2+bx+c,
根据题意得c=2a+b+c=19a+3b+c=5,解得a=1b=-2c=2,
所以抛物线解析式为y=x2-2x+2;
(2)设抛物线解析式为y=ax2+c,
根据题意得a+c=-24a+c=0,解得a=23b=-83,
所以抛物线解析式为y=23x2-83.
【解答】
解:(1)设抛物线解析式为y=ax2+bx+c,
根据题意得c=2a+b+c=19a+3b+c=5,解得a=1b=-2c=2,
所以抛物线解析式为y=x2-2x+2;
(2)设抛物线解析式为y=ax2+c,
根据题意得a+c=-24a+c=0,解得a=23b=-83,
所以抛物线解析式为y=23x2-83.
21.
【答案】
解:根据题意,
得4a-4+c=-5,a+2+c=4,
解得a=-1,c=3,
即这个二次函数的解析式为y=-x2+2x+3.
【解答】
解:根据题意,
得4a-4+c=-5,a+2+c=4,
解得a=-1,c=3,
即这个二次函数的解析式为y=-x2+2x+3.
22.
【答案】
解:设二次函数的解析式为y=a(x-1)2-3.
∵ 点(2,0)在二次函数图像上,
∴ a(2-1)2-3=0,解得:a=3,
∴ 这个二次函数的解析式为y=3(x-1)2-3,
即y=3x2-6x.
【解答】
解:设二次函数的解析式为y=a(x-1)2-3.
∵ 点(2,0)在二次函数图像上,
∴ a(2-1)2-3=0,解得:a=3,
∴ 这个二次函数的解析式为y=3(x-1)2-3,
即y=3x2-6x.
23.
【答案】
解:设二次函数解析式为y=ax2+bx+c(a≠0),
∵ 二次函数的图象经过(1,?-1)、(0,?-1),(-1,?13)三点,
∴ a+b+c=-1c=-1a-b+c=13,
解得:a=7b=-7c=-1.
则该二次函数的解析式是:y=7x2-7x-1.
【解答】
解:设二次函数解析式为y=ax2+bx+c(a≠0),
∵ 二次函数的图象经过(1,?-1)、(0,?-1),(-1,?13)三点,
∴ a+b+c=-1c=-1a-b+c=13,
解得:a=7b=-7c=-1.
则该二次函数的解析式是:y=7x2-7x-1.
24.
【答案】
解:对称轴为直线x=--4a2a=2,
∵ 函数图象与经过点A(1,?0),B(x2,?0),
∴ B(3,?0),AB=3-1=2,
令x=0,则y=b,
∴ S△ABC=12×2?b=2,
∴ b=2,
把A(1,?0)代入二次函数解析式得,a-4a+2=0,
解得a=23,
∴ 二次函数的解析式为:y=23x2-83x+2.
【解答】
解:对称轴为直线x=--4a2a=2,
∵ 函数图象与经过点A(1,?0),B(x2,?0),
∴ B(3,?0),AB=3-1=2,
令x=0,则y=b,
∴ S△ABC=12×2?b=2,
∴ b=2,
把A(1,?0)代入二次函数解析式得,a-4a+2=0,
解得a=23,
∴ 二次函数的解析式为:y=23x2-83x+2.
25.
【答案】
解:(1)由题意得a-b+c=0c=-34a+2b+c=3,
解得a=2b=-1c=-3.
所以这个抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2(x-14)-258,
所以抛物线的开口向上,对称轴为x=14,顶点坐标为(14,?-258)
【解答】
解:(1)由题意得a-b+c=0c=-34a+2b+c=3,
解得a=2b=-1c=-3.
所以这个抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2(x-14)-258,
所以抛物线的开口向上,对称轴为x=14,顶点坐标为(14,?-258)
26.
【答案】
y=15x2-85x+3(答案不唯一).
【解答】
解:此题答案不唯一
设所求解析式为y=a(x-x1)(x-x2),(其中x1其图象与x轴两交点分别是A(x1,?0),B(x2,?0),与y轴交点坐标是(0,?ax1x2).
因为交点式a(x-x1)(x-x2),
又因为与y轴交点的横坐标为0,
所以a(0+x1)(0+x2),也就是ax1x2,
∵ 抛物线对称轴是直线x=4,
∴ x2-4=4-x1,即:x1+x2=8 ①
∵ S△ABC=3,∴ (x2-x1)?|ax1x2|=6,即:x2-x1=6|ax1x2|②
①②两式相加减,可得:x2=4+3|ax1x2|,
x1=4-3|ax1x2|,
∵ x1,x2是整数,ax1x2也是整数,
∴ ax1x2是3的约数,共可取值为:±1,±3.
当ax1x2=±1时,x2=7,x1=1,a=±17
当ax1x2=±3时,x2=5,x1=3,a=±15
因此,所求解析式为:y=±17(x-7)(x-1)或y=±15(x-5)(x-3)
即:y1=17x2-87x+1,
y2=-17x2+87x-1.
y3=15x2-85x+3,
y4=-15x2+85x-3.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
1. 顶点是(-2,?1),开口方向,形状与抛物线y=12x2相同的抛物线是( )
A.y=12(x+2)2+1 B.y=12(x-2)2+1
C.y=13(x-2)2+1 D.y=-12(x+2)2+1
?
2. 已知二次函数的图象如图所示,则这个二次函数的表达式为(? ? ? ? )
A.y=x2-2x+3 B.y=x2-2x-3 C.y=x2+2x-3 D.y=x2+2x+3
?
3. 顶点为(6,?0),开口向下,开口的大小与函数y=13x2的图象相同的抛物线所对应的函数是( )
A.y=13(x+6)2 B.y=13(x-6)2 C.y=-13(x+6)2 D.y=-13(x-6)2
?
4. 如图,抛物线的函数表达式是( )
A.y=x2-x+2 B.y=x2+x+2 C.y=-x2-x+2 D.y=-x2+x+2
?
5. 下表是变量x与y的一组对应值:
x
-2
-1
0
1
2
3
y
1
-0.5
-1
-0.5
1
3.5
从这组数据看,y与x的函数关系是( )
A.正比例函数 B.常数项不为零的一次函数
C.二次函数 D.反比例函数
?6. 抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
A.y=x2-x-2 B.y=-12x2-12x+2
C.y=-12x2-12x+1 D.y=-x2+x+2
?
7. 一个二次函数,当x=0时,y=-5;当x=-1时,y=-4;当x=-2时,y=5,则这个二次函数的关系式是( )
A.y=4x2+3x-5 B.y=2x2+x+5 C.y=2x2-x+5 D.y=2x2+x-5
?
8. 若所求的二次函数图象与抛物线y=2x2-4x-1有相同的顶点,并且在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,则所求二次函数的解析式为(? ? ? ? )
A.y=-x2+2x+4 B.y=-ax2-2ax-3(a>0)
C.y=-2x2-4x-5 D.y=ax2-2ax+a-3(a<0)
?
9. 若a,b,c满足a+b+c=0,a-b+c=0,则关于x的方程ax2+bx+c=0a≠0的解是(? ? ? ? )
A.1,0 B.-1,0 C.1,-1 D.无法确定
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
10. 已知:二次函数的图象过A(1,?0),B(k,?0),C(0,?k)(k≠1).若D是抛物线的顶点,且△ABD是直角三角形,则k=________.
?
11. 二次函数y=x2-2mx+m2-1经过原点,则此二次函数的解析式为________.
?
12. 已知抛物线y=ax2+bx+c与x轴交于A(-2,?0),B(4,?0)两点,顶点C到x轴的距离为2,则此抛物线的解析式为________.
?
13. 若抛物线y=ax2+bx+c的顶点是A(2,?1),且经过点B(1,?0),则抛物线的函数关系式为________.
?
14. 已知直线 y=x+1 与抛物线 y=ax2+2x+c 相交于点 A(-1,0) 和点 B(2,m)两点.则该抛物线的函数表达式是________.
?
15. 二次函数y=ax2+bx+c的图象经过点(-1,?0),(3,?0),(0,?2),当x=2时,y的值为________.
?
16. 二次函数y=ax2+bx+c经过三个点A(-3,?0)、B(0,?3)、C(2,?-5),则二次函数解析式为________.
?
17. 二次函数的图象经过原点(-1,?-2),且图象与x轴的另一交点到原点的距离为2.则二次函数的解析式为________.
?
18. 如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为________.
三、 解答题 (本题共计 8 小题,共66分 , ) ?
19. 已知二次函数y=ax2+bx+c的图象经过A(-1,?0),B(3,?0),C(0,?-3)三点,求这个二次函数的解析式.
?
20. 根据所给条件求抛物线的解析式:
(1)抛物线过点(0,?2)、(1,?1)、(3,?5);
(2)抛物线关于y轴对称,且过点(1,?-2)和(-2,?0).
?
21. 已知二次函数y=ax2+2x+c的图象经过点(-2,?-5),(1,?4).求这个二次函数的解析式.
?
22. 已知二次函数图像的顶点坐标为(1,?-3),且过点(2,?0),求这个二次函数的解析式.
?
23. 已知一个二次函数的图象经过点(1,?-1),(0,?-1),(-1,?13),求这个二次函数的解析式.
?
24. 已知二次函数y=ax2-4ax+b的图象经过点A(1,?0),B(x2,?0),与y轴正半轴交于C点,且S△ABC=2,
求二次函数的解析式.
?
25. 已知抛物线y=ax2+bx+c经过(-1,?0),(0,?-3),(2,?3)三点.
(1)求这条抛物线的表达式.
(2)写出抛物线的开口方向、对称轴和顶点坐标.
?
26. 有一个二次函数的图象,三位学生分别说出了它的一些特点.
甲:对称轴是直线x=4;
乙:与x轴两交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3;
请写出满足上述全部特点的二次函数解析式.
参考答案
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
1.
【答案】
A
【解答】
解:根据题意得:抛物线解析式为y=12(x+2)2+1,
故选A
2.
【答案】
B
【解答】
解:设二次函数的表达式为y=ax2+bx+c,
抛物线过(-1,?0),(0,?-3),(3,?0),
所以a-b+c=0c=-39a+3b+c=0,
解得a=1,b=-2,c=-3,
这个二次函数的表达式为y=x2-2x-3.
故选B.
3.
【答案】
D
【解答】
解:∵ 一个二次函数的图象开口向下,开口的大小与函数y=13x2的图象相同,
故设该二次函数的解析为y=-13(x-h)2+k,
∴ 该函数的顶点坐标为:(h,?k),
又∵ 该二次函数的顶点为(6,?0),
∴ h=6,k=0,
∴ 该二次函数的解析为y=-13(x-6)2.
故选D.
4.
【答案】
D
【解答】
解:根据题意,设二次函数的表达式为y=ax2+bx+c,
抛物线过(-1,?0),(0,?2),(2,?0),
所以a-b+c=0c=24a+2b+c=0,
解得a=-1,b=1,c=2,
这个二次函数的表达式为y=-x2+x+2.
故选D.
5.
【答案】
C
【解答】
解:观察可知,函数图象关于y轴对称,顶点坐标是(0,?-1),
∴ 设函数解析式为y=ax2-1,
当x=1时,a-1=-0.5,
解得a=12,
y=12x2-1,
所以是二次函数.
故选C.
6.
【答案】
D
【解答】
解:A、由图象可知开口向下,故a<0,此选项错误;
B、抛物线过点(-1,?0),(2,?0),根据抛物线的对称性,顶点的横坐标是12,
而y=-12x2-12x+2的顶点横坐标是--122×(-12)=-12,故此选项错误;
C、y=-12x2-12x+1的顶点横坐标是-12,故此选项错误;
D、y=-x2+x+2的顶点横坐标是12,并且抛物线过点(-1,?0),(2,?0),故此选项正确.
故选D.
7.
【答案】
A
【解答】
解:设二次函数的关系式是y=ax2+bx+c(a≠0),
∵ 当x=0时,y=-5;当x=-1时,y=-4;当x=-2时,y=5,
∴ c=-5①,
a-b+c=-4②,
4a-2b+c=5③,
解由①②③组成的方程组得,a=4,b=3,c=-5,
所以二次函数的关系式为:y=4x2+3x-5.
故选A.
8.
【答案】
D
【解答】
解:抛物线y=2x2-4x-1的顶点坐标为(1,?-3),
根据题意得所求的二次函数的解析式的顶点坐标是(1,?-3),
且抛物线开口向下.
A,抛物线开口向下,顶点坐标是(1,?5),故选项A错误;
B,抛物线开口向下,顶点坐标是(-1,?a-3),故选项B错误;
C,抛物线开口向下,顶点坐标是(-1,?-3),故选项C错误;
D,抛物线开口向下,顶点坐标是(1,?-3),故选项D正确.
故选D.
9.
【答案】
C
【解答】
解:a+b+c=0①,a-b+c=0②,
①-②得,2b=0,所以b=0.
①+②得,2a+2c=0,
所以a+c=0,即a=-c(c≠0).
把b=0代入关于x的方程ax2+bx+c=0得,ax2+c=0,
所以x2=-ca=1,
即x1=1?,?x2=-1.
故选C.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
10.
【答案】
-1或3
【解答】
解:根据题意设二次函数的解析式为y=ax2+bx+k,二次函数的图象过A(1,?0),B(k,?0),
则a+b+k=0ak2+bk+k=0,
解得a=1,b=-k-1;
二次函数的解析式为y=x2-(k+1)x+k,
当k>1时,函数的图象如图1,
对称轴DE为x=k+12,顶点坐标为(k+12,?-(k-1)24),
若△ABD是直角三角形,AD=DB,
则AE=DE,k+12-1=(k-1)24,
解得k=3,
当k<0,函数的图象如图2,
同理求出k=-1;
所以D是抛物线的顶点,且△ABD是直角三角形,则k=-1或3;
故答案为-1或3.
11.
【答案】
y=x2-2x或y=x2+2x
【解答】
解:把(0,?0)代入y=x2-2mx+m2-1得m2-1=0,解得m=1或m=-1,
当m=1时,二次函数的解析式为y=x2-2x;当m=-1时,二次函数的解析式为y=x2+2x,
即二次函数的解析式为y=x2-2x或y=x2+2x.
故答案为y=x2-2x或y=x2+2x.
12.
【答案】
y=-29x2+49x+169或y=29x2-49x-169
【解答】
解:∵ 抛物线y=ax2+bx+c与x轴交于A(-2,?0),B(4,?0)两点,
∴ 抛物线的对称轴为直线x=1,
∵ 顶点C到x轴的距离为2,
∴ C点坐标为(1,?2)或(1,?-2),
设抛物线解析式为y=a(x+2)(x-4),
把C(1,?2)代入得a×3×(-3)=2,解得a=-29,所以此时抛物线解析式为y=-29(x+2)(x-4)=-29x2+49x+169;
把C(1,?-2)代入得a×3×(-3)=-2,解得a=29,所以此时抛物线解析式为y=29(x+2)(x-4)=29x2-49x-169,
∴ 抛物线解析式为y=-29x2+49x+169或y=29x2-49x-169.
故答案为y=-29x2+49x+169或y=29x2-49x-169.
13.
【答案】
y=-x2+4x-3
【解答】
解:设抛物线的解析式为y=a(x-2)2+1,
将B(1,?0)代入y=a(x-2)2+1,
得a=-1,
函数解析式为y=-(x-2)2+1,
展开得y=-x2+4x-3.
故答案为:y=-x2+4x-3.
14.
【答案】
y=-x2+2x+3
【解答】
解:由题知:点B(2,m)在直线y=x+1上,
故m=2+1=3.
∴ 点B(2,3)和点A(-1,0)在抛物线上,
∴ a-2+c=0,4a+4+c=3,
由上述解得:a=-1,c=3,
故解析式为:y=-x2+2x+3.
故答案为:y=-x2+2x+3.
15.
【答案】
2
【解答】
解:如图所示,
∵ 二次函数y=ax2+bx+c的图象经过点(-1,?0),(3,?0)和(0,?2),
∴ a-b+c=0,9a+3b+c=0,c=2,?
解得:a=-23,b=43,c=2.?
则这个二次函数的表达式为y=-23x2+43x+2.
把x=2代入得,y=-23×4+43×2+2=2.
故答案为:2.
16.
【答案】
y=-x2-2x+3
【解答】
解:根据题意,得
9a-3b+c=0c=34a+2b+c=-5,
解得,a=-1b=-2c=3,
∴ 二次函数解析式为y=-x2-2x+3.
故答案是:y=-x2-2x+3.
17.
【答案】
y=2x2+4x或y=-23x2+43x
【解答】
解:根据题意得,与x轴的另一个交点为(2,?0)或(-2,?0),因此要分两种情况:
(1)过点(-2,?0),设y=ax(x+2),则-2=-a,解得:a=2,
∴ 抛物线的解析式为:y=2x2+4x;
(2)过点(2,?0),设y=ax(x-2),则-2=3a,解得:a=-23,
∴ 抛物线的解析式为:y=-23x2+43x.
故答案为y=2x2+4x或y=-23x2+43x.
18.
【答案】
(3-52,?3-52)
【解答】
A的坐标是(1,?0)、C坐标是(0,?1),设出解析式是y=a(x-1)2,把C的坐标代入得:a(-1)2=1,
解得:a=1,
则抛物线的解析式是:y=(x-1)2;
∵ B的坐标是(1,?1),
设OB解析式的解析式是y=kx,则k=1,则OB的解析式是y=x.
根据题意得:y=(x-1)2y=x?,
解得:x=3+52y=3+52?(舍去),或x=3-52y=3-52?.
则D的坐标是:(3-52,?3-52).
三、 解答题 (本题共计 8 小题 ,每题 10 分 ,共计80分 )
19.
【答案】
解:设抛物线的解析式为y=a(x+1)(x-3),
把C(0,?-3)代入得a×1×(-3)=-3,
解得a=1,
所以这个二次函数的解析式为y=(x+1)(x-3)=x2-2x-3.
【解答】
解:设抛物线的解析式为y=a(x+1)(x-3),
把C(0,?-3)代入得a×1×(-3)=-3,
解得a=1,
所以这个二次函数的解析式为y=(x+1)(x-3)=x2-2x-3.
20.
【答案】
解:(1)设抛物线解析式为y=ax2+bx+c,
根据题意得c=2a+b+c=19a+3b+c=5,解得a=1b=-2c=2,
所以抛物线解析式为y=x2-2x+2;
(2)设抛物线解析式为y=ax2+c,
根据题意得a+c=-24a+c=0,解得a=23b=-83,
所以抛物线解析式为y=23x2-83.
【解答】
解:(1)设抛物线解析式为y=ax2+bx+c,
根据题意得c=2a+b+c=19a+3b+c=5,解得a=1b=-2c=2,
所以抛物线解析式为y=x2-2x+2;
(2)设抛物线解析式为y=ax2+c,
根据题意得a+c=-24a+c=0,解得a=23b=-83,
所以抛物线解析式为y=23x2-83.
21.
【答案】
解:根据题意,
得4a-4+c=-5,a+2+c=4,
解得a=-1,c=3,
即这个二次函数的解析式为y=-x2+2x+3.
【解答】
解:根据题意,
得4a-4+c=-5,a+2+c=4,
解得a=-1,c=3,
即这个二次函数的解析式为y=-x2+2x+3.
22.
【答案】
解:设二次函数的解析式为y=a(x-1)2-3.
∵ 点(2,0)在二次函数图像上,
∴ a(2-1)2-3=0,解得:a=3,
∴ 这个二次函数的解析式为y=3(x-1)2-3,
即y=3x2-6x.
【解答】
解:设二次函数的解析式为y=a(x-1)2-3.
∵ 点(2,0)在二次函数图像上,
∴ a(2-1)2-3=0,解得:a=3,
∴ 这个二次函数的解析式为y=3(x-1)2-3,
即y=3x2-6x.
23.
【答案】
解:设二次函数解析式为y=ax2+bx+c(a≠0),
∵ 二次函数的图象经过(1,?-1)、(0,?-1),(-1,?13)三点,
∴ a+b+c=-1c=-1a-b+c=13,
解得:a=7b=-7c=-1.
则该二次函数的解析式是:y=7x2-7x-1.
【解答】
解:设二次函数解析式为y=ax2+bx+c(a≠0),
∵ 二次函数的图象经过(1,?-1)、(0,?-1),(-1,?13)三点,
∴ a+b+c=-1c=-1a-b+c=13,
解得:a=7b=-7c=-1.
则该二次函数的解析式是:y=7x2-7x-1.
24.
【答案】
解:对称轴为直线x=--4a2a=2,
∵ 函数图象与经过点A(1,?0),B(x2,?0),
∴ B(3,?0),AB=3-1=2,
令x=0,则y=b,
∴ S△ABC=12×2?b=2,
∴ b=2,
把A(1,?0)代入二次函数解析式得,a-4a+2=0,
解得a=23,
∴ 二次函数的解析式为:y=23x2-83x+2.
【解答】
解:对称轴为直线x=--4a2a=2,
∵ 函数图象与经过点A(1,?0),B(x2,?0),
∴ B(3,?0),AB=3-1=2,
令x=0,则y=b,
∴ S△ABC=12×2?b=2,
∴ b=2,
把A(1,?0)代入二次函数解析式得,a-4a+2=0,
解得a=23,
∴ 二次函数的解析式为:y=23x2-83x+2.
25.
【答案】
解:(1)由题意得a-b+c=0c=-34a+2b+c=3,
解得a=2b=-1c=-3.
所以这个抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2(x-14)-258,
所以抛物线的开口向上,对称轴为x=14,顶点坐标为(14,?-258)
【解答】
解:(1)由题意得a-b+c=0c=-34a+2b+c=3,
解得a=2b=-1c=-3.
所以这个抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2(x-14)-258,
所以抛物线的开口向上,对称轴为x=14,顶点坐标为(14,?-258)
26.
【答案】
y=15x2-85x+3(答案不唯一).
【解答】
解:此题答案不唯一
设所求解析式为y=a(x-x1)(x-x2),(其中x1
因为交点式a(x-x1)(x-x2),
又因为与y轴交点的横坐标为0,
所以a(0+x1)(0+x2),也就是ax1x2,
∵ 抛物线对称轴是直线x=4,
∴ x2-4=4-x1,即:x1+x2=8 ①
∵ S△ABC=3,∴ (x2-x1)?|ax1x2|=6,即:x2-x1=6|ax1x2|②
①②两式相加减,可得:x2=4+3|ax1x2|,
x1=4-3|ax1x2|,
∵ x1,x2是整数,ax1x2也是整数,
∴ ax1x2是3的约数,共可取值为:±1,±3.
当ax1x2=±1时,x2=7,x1=1,a=±17
当ax1x2=±3时,x2=5,x1=3,a=±15
因此,所求解析式为:y=±17(x-7)(x-1)或y=±15(x-5)(x-3)
即:y1=17x2-87x+1,
y2=-17x2+87x-1.
y3=15x2-85x+3,
y4=-15x2+85x-3.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
