五年级上册数学课件-数学好玩《尝试与猜测》北师大版 (共68张PPT)
文档属性
| 名称 | 五年级上册数学课件-数学好玩《尝试与猜测》北师大版 (共68张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 14:24:22 | ||
图片预览









文档简介
(共74张PPT)
大约一千五百年前,我国古代数学名著《孙子算经》中记载着许多有趣的数学名题
。
北师大五年级数学上册
尝试与猜测
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
zhì
雉:野鸡。
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
(3)同学们先来猜一猜鸡、兔可能各有多少只?
鸡和兔共有35只,鸡和兔的脚共94只。
(1)你从中发现了哪些数学信息?
(2)这道题里还有隐藏的数学信息吗??
每只兔有4只脚,每只鸡有2只脚。
解题的关键
一只鸡(
)条腿,一只兔(
)条腿
.
2
4
一只鸡一只兔,共(
)个头,(
)条腿?
2
6
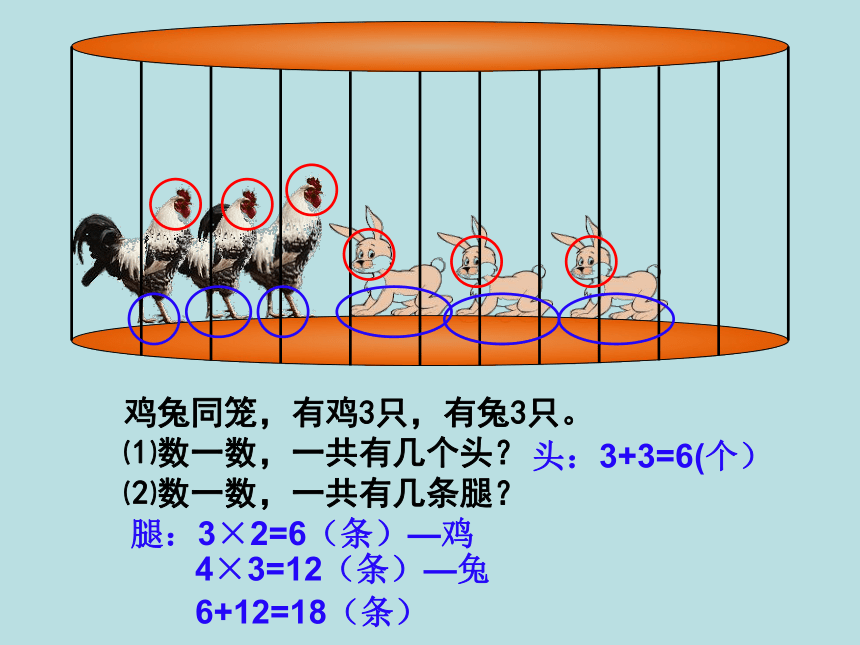
鸡兔同笼,有鸡3只,有兔3只。
⑴数一数,一共有几个头?
⑵数一数,一共有几条腿?
头:3+3=6(个)
腿:3×2=6(条)—鸡
4×3=12(条)—兔
6+12=18(条)
鸡兔同笼,
数它们的头共有2个,
数它们的腿共有6条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有2个,
数它们的腿共有6条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有8条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有8条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有10条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有10条。
想想有几只鸡?有几只兔?
头数
6
6
6
6
6
鸡/只
兔/只
脚/只
16
18
1
1
2
5
3
4
2
3
4
5
20
14
22
(4)请同学们借助表格,整理一下我们的解题过程。
(1)如果鸡兔共6只,共有22只脚,尝试猜测一下鸡、兔各有多少只?
(2)鸡兔共6只不变,脚数变为20只脚,鸡兔各几只?你是怎猜测出来的?
(3)鸡兔共6只不变,脚数还有其它情况吗?鸡兔的只数呢?
头数
6
6
6
6
6
鸡/只
兔/只
脚/只
16
18
1
1
2
5
3
4
2
3
4
5
20
14
22
从下表中你发现了什么规律?
1、鸡的只数在逐一增多。
2、兔的只数在逐一减少;脚的只数也在减少。
3、鸡增加一只兔减少一只,脚数减少两只。
☆
鸡兔的只数是固定的,每减少一只兔就要增加一只鸡,脚的总数就减少两条。
1、笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
试一试
头数
35
35
35
35
35
35
鸡/只
兔/只
脚/只
答:鸡有
只,兔有
只。
23
12
鸡兔同笼,共有5个头,
14条腿。笼子里有几只鸡?有几只兔?
1、画图法
5×2=10(条)
14-10=4(条)
少画了4条腿,补上,怎样补?
可以全部看成是鸡:
4÷2=2(只)
补上2个2条腿。
兔子2只,鸡3只
5×4=20(条)
20-14=6(条)
多画了6条腿,擦去,怎样擦去?
也可以全部看成是兔:
5×4=20(条)
20-14=6(条)
多画了6条腿,擦去,怎样擦去?
也可以全部看成是兔:
6÷2=3(只)
兔子2只,鸡3只
擦去3个2条腿
⑴先画5只兔,5×4=20(条)
⑵多画了6条腿,20-14=6(条)
也可以先假设全部是兔:
⑶擦去6条腿,把兔换成鸡。
⑴先画5只兔,5×2=10(条)
⑵少画了4条腿,14-10=4(条)
⑶少画的补上,把鸡换成兔。
先假设全部是鸡:
假设法
2、列表法:
鸡的知数
兔的知数
共有腿数
5
0
10
鸡的知数
5
兔的知数
0
共有腿数
10
4
1
12
鸡的知数
5
4
兔的知数
0
1
共有腿数
10
12
3
2
14
鸡的知数
5
4
3
兔的知数
0
1
2
共有腿数
10
12
14
2
3
16
鸡的知数
5
4
3
2
兔的知数
0
1
2
3
共有腿数
10
12
14
16
1
4
18
鸡的知数
5
4
3
2
1
兔的知数
0
1
2
3
4
共有腿数
10
12
14
16
18
0
5
20
列表法:
鸡的知数
5
4
3
2
1
0
兔的知数
0
1
2
3
4
5
共有腿数
10
12
14
16
18
20
你发现了什么规律?
鸡兔同笼,有9个头,26条腿。鸡和兔各有几只?
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》。
1、与同伴说一说你的想法。
我早听说过“鸡兔同笼”问题,就是不会做。
有9个头会有哪些可能呢?列表试一试。
2、笑笑是这么做的,你看懂了吗?与同伴交流。
鸡有几只
兔有几只
腿有多少条
1
8
34
×
2
7
32
×
3
6
30
×
4
5
28
×
5
4
26
√
也可以先假设有1只兔8只鸡,请你列表试一试。
一共有9个头,假设有1只鸡,应该有8只兔,那鸡和兔的腿数是34条,不对……
3、从列表中,你还发现了什么?与同伴交流。
我发现鸡增加1只,兔减少1只,腿就会减少2条……
只要按照这个步骤做下去,不管头数和腿数是多少,都能解决……
鸡有几只
兔有几只
腿有多少条
1
8
34
×
2
7
32
×
3
6
30
×
4
5
28
×
5
4
26
√
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
读一读,你知道这道题的意思吗?你能解决这个问题吗?
还从有1只鸡开始一个一个地试……
鸡有几只
兔有几只
腿有多少条
1
34
138
×
2
33
136
×
3
32
134
×
4
31
132
×
…
…
…
23
12
94
√
逐一列举法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
读一读,你知道这道题的意思?你能解决这个问题吗?
我是这么做的……
鸡有几只
兔有几只
腿有多少条
1
34
138
×
10
25
120
×
20
15
100
×
25
10
90
×
24
11
92
×
23
12
94
√
跳跃列举法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
读一读,你知道这道题的意思?你能解决这个问题吗?
我先假设鸡和兔的只数差不多……
鸡有几只
兔有几只
腿有多少条
17
18
106
×
20
15
100
×
22
13
96
×
23
12
94
√
取中列举法
鸡兔同笼不是只解决鸡与兔的问题,它是一类问题的统称。生活中许多问题都可以用解决鸡兔同笼问题的方法来解决。
已知:共有54人,共租10条船,每条船都坐满。
大船乘6人
小船乘4人
求:
大、小船各租几条?
鸡兔的总头数
鸡兔的总脚数
走进生活
小明的储蓄罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
走进生活
你知道古人是怎样解决“鸡兔同笼”问题的吗?
(1)假如让鸡抬起一只脚,
兔子抬起两只脚
,还
有94÷2=47只脚。
(2)这时每只鸡一只脚,
每只兔子两只脚,笼子里只要有一只兔子,则脚的总数就比头的总数多1。
(3)这时脚的总数与头的总数之差47-35=12,就是兔子的只数。
阅
读
资
料
乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元,1角和5角的硬币各有多少枚?请你用列表的方法解决问题。
1角/枚
5角/枚
总值/元
…
…
…
走进生活
列表法
假设法
方程法
解决鸡兔同笼问题的方法有:
画图法
鸡兔同笼,共有5个头,
14条腿。笼子里有几只鸡?有几只兔?
2、有龟和鹤共40只,龟的脚和鹤的脚共有112条。龟、鹤各有几只?
日本的龟鹤问题
试一试
头数
40
40
40
40
40
40
鹤/只
龟/只
脚/只
答:鹤有
只,龟有
只。
24
16
菜市场里真热闹,
鸡兔同笼喔喔叫。
数数头儿有8个,
数数腿儿26。
可知鸡兔各多少?
2×8=16(条)
26-16=10(条)
画图法
2×8=16(条)
26-16=10(条)
兔子:10÷2=5(只)
鸡:8-5=3(只)
假
设
法
怎样验证结果是正确的?
画图法
假设笼子里都是鸡,那么应有多少条腿?
8×2=16(条)
这样比题中条件少了多少条腿?
26-16=10(条)
为什么会少了10条腿呢?
因为,一只兔比一只鸡多2只脚,
有多少只兔能相差10条腿?
10÷2=5(只)
所以有5只兔
8-5=3(只)
有3只鸡。
(兔)的只数
8
7
6
5
(鸡)的只数
0
1
2
3
共有腿数
32
30
28
26
(鸡)的只数
8
7
6
5
4
3
(兔)的只数
0
1
2
3
4
5
共有腿数
16
18
20
22
24
26
想一想:
当算出共有的腿数多了,说明什么?怎么办呢?当算出的共有腿数少了呢?
.尝试与实践:
鸡兔同笼,有20头,54条腿,鸡兔各多少只?
1.出示例题:
师:同学们有兴趣解决这个古老的问题吗?
师:只要‘‘细心观察,不断的尝试”.相信同学们.
师:现在分组学习,每八人为一小组讨论解决的方法.
第一组表格:
第二组表格:
动物只数
鸡的只数
兔的只数
腿的只数
20
1
19
78
20
5
15
70
20
10
10
60
20
15
5
50
20
14
6
52
20
13
7
54
第三组表格:
动物只数
鸡的只数
兔的只数
腿的只数
20
10
10
60
20
11
9
58
20
13
7
54
师:你们觉得那种方案你最喜欢?
生:我们组还有好方法,我们画出它们的腿进行尝试.
教师小结:
师:太棒了,真是太棒了!画图法也是一种直观形象的好方法,时间关系,我们这节课先掌握列表的方法,将画图法布置为我们今天的作业尝试。
师:通过评比,你们觉得哪个组的办法最好?
四.名解欣赏:
师:你们知道我们今天研究的鸡兔问题最早记录在哪本书上吗?古代有一个大数学家孙子想出的一种更奇特、更简洁的方法,你知道吗?
孙子巧解“鸡兔同笼”
大约在一千五百年前,大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?同学们,你会解答这个问题吗?你知道孙子是如何解答这个“鸡兔同笼”问题的?
解析:
原来孙子提出了大胆的设想。他假设砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独脚鸡”,而每只兔就变成了“双脚兔”。这样,“独脚鸡”和“双脚兔”的脚就由94只变成了47只;而每只“鸡”的头数与脚数之比变为1:1,每只“兔”的头数与脚数之比变为1:2。由此可知,有一只“双脚兔”,脚的数量就会比头的数量多1。所以,“独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差,就是兔子的只数,即:47-35=12(只);鸡的数量就是:35-12=23(只)。
当然,这道题还可以用方程来解答。
先设兔的只数(也就是头数)是x,因为“鸡头+兔头=35”,所以“鸡头=35-x”。
由此可知,有x只兔,应该有4x只兔脚,而鸡的只数是(35-x),所以应该有2×(35-x)只鸡脚。现在已知鸡兔的脚总共是94只,因此,我们可以列出下面的关系式:
4x+2×(35-x)=94
x=12
于是可以算出鸡的只数是35-12=23。
寄一封平信(20克以内)本市要贴6角的邮票,
外埠(bu)要贴8角的邮票。小明买了两种邮票
一共花了5元,分别买了多少张?
6角
8角
共花多少元
1张
(6角)
4张
5张
6张
7张
3张
2张
(12角)
(18角)
(24角)
(30角)
(36角)
(42角)
(44角)
(38角)
(32角)
(26角)
(20角)
(14角)
(8角)
1张
4张
5元
5元
小方有2分、5分硬币共10枚,共有32分。2分、5分硬币各有几枚?
2分
2分
2分
2分
2分
2分
2分
2分
2分
2分
2×10=20(分)
32—20=12(分)
5-2=3(分)
12分
拆成几个
?
几分
12÷3=4(个)
5分
3分
3分
3分
3分
10—4=6(个)
2分
有龟和鹤共7只,龟的腿和鹤的腿共有20条,龟和鹤各有几只?
全班一共有38人,共租8条船,每条船都坐满了,大小船各租了几条?
◆自行车和三轮车放在同一个车棚里,数数一共有8辆,数数轮子一共有19个。问:自行车有几辆?三轮车有几辆?
◆一只蛐蛐6条腿,一只蜘蛛8条腿,现有蛐蛐和蜘蛛共7只,共有48条腿,问:蛐蛐几只?蜘蛛几只?
鸵鸟和斑马共10个头,32条腿,鸵鸟有几只?斑马有几匹?
乒乓球比赛,有8个球案在进行单打、双打比赛,一共有22人正在比赛。单打的球案有几张?双打的球案有几张?
按
砍足法:(《孙子算经》中记载的方法)
假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”。这样,(1)鸡和兔的脚的总数就由26只变成了13只;(2)如果笼子里有一只兔子,则脚的总数就比头的总数多1。因此,脚的总只数13与总头数8的差,就是兔子的只数,即13-8=5(只)。显然,鸡的只数就是5只了。
大约一千五百年前,我国古代数学名著《孙子算经》中记载着许多有趣的数学名题
。
北师大五年级数学上册
尝试与猜测
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
zhì
雉:野鸡。
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
(3)同学们先来猜一猜鸡、兔可能各有多少只?
鸡和兔共有35只,鸡和兔的脚共94只。
(1)你从中发现了哪些数学信息?
(2)这道题里还有隐藏的数学信息吗??
每只兔有4只脚,每只鸡有2只脚。
解题的关键
一只鸡(
)条腿,一只兔(
)条腿
.
2
4
一只鸡一只兔,共(
)个头,(
)条腿?
2
6
鸡兔同笼,有鸡3只,有兔3只。
⑴数一数,一共有几个头?
⑵数一数,一共有几条腿?
头:3+3=6(个)
腿:3×2=6(条)—鸡
4×3=12(条)—兔
6+12=18(条)
鸡兔同笼,
数它们的头共有2个,
数它们的腿共有6条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有2个,
数它们的腿共有6条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有8条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有8条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有10条。
想想有几只鸡?有几只兔?
鸡兔同笼,
数它们的头共有3个,
数它们的腿共有10条。
想想有几只鸡?有几只兔?
头数
6
6
6
6
6
鸡/只
兔/只
脚/只
16
18
1
1
2
5
3
4
2
3
4
5
20
14
22
(4)请同学们借助表格,整理一下我们的解题过程。
(1)如果鸡兔共6只,共有22只脚,尝试猜测一下鸡、兔各有多少只?
(2)鸡兔共6只不变,脚数变为20只脚,鸡兔各几只?你是怎猜测出来的?
(3)鸡兔共6只不变,脚数还有其它情况吗?鸡兔的只数呢?
头数
6
6
6
6
6
鸡/只
兔/只
脚/只
16
18
1
1
2
5
3
4
2
3
4
5
20
14
22
从下表中你发现了什么规律?
1、鸡的只数在逐一增多。
2、兔的只数在逐一减少;脚的只数也在减少。
3、鸡增加一只兔减少一只,脚数减少两只。
☆
鸡兔的只数是固定的,每减少一只兔就要增加一只鸡,脚的总数就减少两条。
1、笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
试一试
头数
35
35
35
35
35
35
鸡/只
兔/只
脚/只
答:鸡有
只,兔有
只。
23
12
鸡兔同笼,共有5个头,
14条腿。笼子里有几只鸡?有几只兔?
1、画图法
5×2=10(条)
14-10=4(条)
少画了4条腿,补上,怎样补?
可以全部看成是鸡:
4÷2=2(只)
补上2个2条腿。
兔子2只,鸡3只
5×4=20(条)
20-14=6(条)
多画了6条腿,擦去,怎样擦去?
也可以全部看成是兔:
5×4=20(条)
20-14=6(条)
多画了6条腿,擦去,怎样擦去?
也可以全部看成是兔:
6÷2=3(只)
兔子2只,鸡3只
擦去3个2条腿
⑴先画5只兔,5×4=20(条)
⑵多画了6条腿,20-14=6(条)
也可以先假设全部是兔:
⑶擦去6条腿,把兔换成鸡。
⑴先画5只兔,5×2=10(条)
⑵少画了4条腿,14-10=4(条)
⑶少画的补上,把鸡换成兔。
先假设全部是鸡:
假设法
2、列表法:
鸡的知数
兔的知数
共有腿数
5
0
10
鸡的知数
5
兔的知数
0
共有腿数
10
4
1
12
鸡的知数
5
4
兔的知数
0
1
共有腿数
10
12
3
2
14
鸡的知数
5
4
3
兔的知数
0
1
2
共有腿数
10
12
14
2
3
16
鸡的知数
5
4
3
2
兔的知数
0
1
2
3
共有腿数
10
12
14
16
1
4
18
鸡的知数
5
4
3
2
1
兔的知数
0
1
2
3
4
共有腿数
10
12
14
16
18
0
5
20
列表法:
鸡的知数
5
4
3
2
1
0
兔的知数
0
1
2
3
4
5
共有腿数
10
12
14
16
18
20
你发现了什么规律?
鸡兔同笼,有9个头,26条腿。鸡和兔各有几只?
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》。
1、与同伴说一说你的想法。
我早听说过“鸡兔同笼”问题,就是不会做。
有9个头会有哪些可能呢?列表试一试。
2、笑笑是这么做的,你看懂了吗?与同伴交流。
鸡有几只
兔有几只
腿有多少条
1
8
34
×
2
7
32
×
3
6
30
×
4
5
28
×
5
4
26
√
也可以先假设有1只兔8只鸡,请你列表试一试。
一共有9个头,假设有1只鸡,应该有8只兔,那鸡和兔的腿数是34条,不对……
3、从列表中,你还发现了什么?与同伴交流。
我发现鸡增加1只,兔减少1只,腿就会减少2条……
只要按照这个步骤做下去,不管头数和腿数是多少,都能解决……
鸡有几只
兔有几只
腿有多少条
1
8
34
×
2
7
32
×
3
6
30
×
4
5
28
×
5
4
26
√
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
读一读,你知道这道题的意思吗?你能解决这个问题吗?
还从有1只鸡开始一个一个地试……
鸡有几只
兔有几只
腿有多少条
1
34
138
×
2
33
136
×
3
32
134
×
4
31
132
×
…
…
…
23
12
94
√
逐一列举法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
读一读,你知道这道题的意思?你能解决这个问题吗?
我是这么做的……
鸡有几只
兔有几只
腿有多少条
1
34
138
×
10
25
120
×
20
15
100
×
25
10
90
×
24
11
92
×
23
12
94
√
跳跃列举法
《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
读一读,你知道这道题的意思?你能解决这个问题吗?
我先假设鸡和兔的只数差不多……
鸡有几只
兔有几只
腿有多少条
17
18
106
×
20
15
100
×
22
13
96
×
23
12
94
√
取中列举法
鸡兔同笼不是只解决鸡与兔的问题,它是一类问题的统称。生活中许多问题都可以用解决鸡兔同笼问题的方法来解决。
已知:共有54人,共租10条船,每条船都坐满。
大船乘6人
小船乘4人
求:
大、小船各租几条?
鸡兔的总头数
鸡兔的总脚数
走进生活
小明的储蓄罐里有1角和5角的硬币共27枚,价值5.1元,1角和5角的硬币各有多少枚?
走进生活
你知道古人是怎样解决“鸡兔同笼”问题的吗?
(1)假如让鸡抬起一只脚,
兔子抬起两只脚
,还
有94÷2=47只脚。
(2)这时每只鸡一只脚,
每只兔子两只脚,笼子里只要有一只兔子,则脚的总数就比头的总数多1。
(3)这时脚的总数与头的总数之差47-35=12,就是兔子的只数。
阅
读
资
料
乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元,1角和5角的硬币各有多少枚?请你用列表的方法解决问题。
1角/枚
5角/枚
总值/元
…
…
…
走进生活
列表法
假设法
方程法
解决鸡兔同笼问题的方法有:
画图法
鸡兔同笼,共有5个头,
14条腿。笼子里有几只鸡?有几只兔?
2、有龟和鹤共40只,龟的脚和鹤的脚共有112条。龟、鹤各有几只?
日本的龟鹤问题
试一试
头数
40
40
40
40
40
40
鹤/只
龟/只
脚/只
答:鹤有
只,龟有
只。
24
16
菜市场里真热闹,
鸡兔同笼喔喔叫。
数数头儿有8个,
数数腿儿26。
可知鸡兔各多少?
2×8=16(条)
26-16=10(条)
画图法
2×8=16(条)
26-16=10(条)
兔子:10÷2=5(只)
鸡:8-5=3(只)
假
设
法
怎样验证结果是正确的?
画图法
假设笼子里都是鸡,那么应有多少条腿?
8×2=16(条)
这样比题中条件少了多少条腿?
26-16=10(条)
为什么会少了10条腿呢?
因为,一只兔比一只鸡多2只脚,
有多少只兔能相差10条腿?
10÷2=5(只)
所以有5只兔
8-5=3(只)
有3只鸡。
(兔)的只数
8
7
6
5
(鸡)的只数
0
1
2
3
共有腿数
32
30
28
26
(鸡)的只数
8
7
6
5
4
3
(兔)的只数
0
1
2
3
4
5
共有腿数
16
18
20
22
24
26
想一想:
当算出共有的腿数多了,说明什么?怎么办呢?当算出的共有腿数少了呢?
.尝试与实践:
鸡兔同笼,有20头,54条腿,鸡兔各多少只?
1.出示例题:
师:同学们有兴趣解决这个古老的问题吗?
师:只要‘‘细心观察,不断的尝试”.相信同学们.
师:现在分组学习,每八人为一小组讨论解决的方法.
第一组表格:
第二组表格:
动物只数
鸡的只数
兔的只数
腿的只数
20
1
19
78
20
5
15
70
20
10
10
60
20
15
5
50
20
14
6
52
20
13
7
54
第三组表格:
动物只数
鸡的只数
兔的只数
腿的只数
20
10
10
60
20
11
9
58
20
13
7
54
师:你们觉得那种方案你最喜欢?
生:我们组还有好方法,我们画出它们的腿进行尝试.
教师小结:
师:太棒了,真是太棒了!画图法也是一种直观形象的好方法,时间关系,我们这节课先掌握列表的方法,将画图法布置为我们今天的作业尝试。
师:通过评比,你们觉得哪个组的办法最好?
四.名解欣赏:
师:你们知道我们今天研究的鸡兔问题最早记录在哪本书上吗?古代有一个大数学家孙子想出的一种更奇特、更简洁的方法,你知道吗?
孙子巧解“鸡兔同笼”
大约在一千五百年前,大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?同学们,你会解答这个问题吗?你知道孙子是如何解答这个“鸡兔同笼”问题的?
解析:
原来孙子提出了大胆的设想。他假设砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独脚鸡”,而每只兔就变成了“双脚兔”。这样,“独脚鸡”和“双脚兔”的脚就由94只变成了47只;而每只“鸡”的头数与脚数之比变为1:1,每只“兔”的头数与脚数之比变为1:2。由此可知,有一只“双脚兔”,脚的数量就会比头的数量多1。所以,“独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差,就是兔子的只数,即:47-35=12(只);鸡的数量就是:35-12=23(只)。
当然,这道题还可以用方程来解答。
先设兔的只数(也就是头数)是x,因为“鸡头+兔头=35”,所以“鸡头=35-x”。
由此可知,有x只兔,应该有4x只兔脚,而鸡的只数是(35-x),所以应该有2×(35-x)只鸡脚。现在已知鸡兔的脚总共是94只,因此,我们可以列出下面的关系式:
4x+2×(35-x)=94
x=12
于是可以算出鸡的只数是35-12=23。
寄一封平信(20克以内)本市要贴6角的邮票,
外埠(bu)要贴8角的邮票。小明买了两种邮票
一共花了5元,分别买了多少张?
6角
8角
共花多少元
1张
(6角)
4张
5张
6张
7张
3张
2张
(12角)
(18角)
(24角)
(30角)
(36角)
(42角)
(44角)
(38角)
(32角)
(26角)
(20角)
(14角)
(8角)
1张
4张
5元
5元
小方有2分、5分硬币共10枚,共有32分。2分、5分硬币各有几枚?
2分
2分
2分
2分
2分
2分
2分
2分
2分
2分
2×10=20(分)
32—20=12(分)
5-2=3(分)
12分
拆成几个
?
几分
12÷3=4(个)
5分
3分
3分
3分
3分
10—4=6(个)
2分
有龟和鹤共7只,龟的腿和鹤的腿共有20条,龟和鹤各有几只?
全班一共有38人,共租8条船,每条船都坐满了,大小船各租了几条?
◆自行车和三轮车放在同一个车棚里,数数一共有8辆,数数轮子一共有19个。问:自行车有几辆?三轮车有几辆?
◆一只蛐蛐6条腿,一只蜘蛛8条腿,现有蛐蛐和蜘蛛共7只,共有48条腿,问:蛐蛐几只?蜘蛛几只?
鸵鸟和斑马共10个头,32条腿,鸵鸟有几只?斑马有几匹?
乒乓球比赛,有8个球案在进行单打、双打比赛,一共有22人正在比赛。单打的球案有几张?双打的球案有几张?
按
砍足法:(《孙子算经》中记载的方法)
假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”。这样,(1)鸡和兔的脚的总数就由26只变成了13只;(2)如果笼子里有一只兔子,则脚的总数就比头的总数多1。因此,脚的总只数13与总头数8的差,就是兔子的只数,即13-8=5(只)。显然,鸡的只数就是5只了。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
