第26章 本章小结 专题复习 二次函数——二次函数与相似的结合 教案
文档属性
| 名称 | 第26章 本章小结 专题复习 二次函数——二次函数与相似的结合 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 287.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 13:49:05 | ||
图片预览

文档简介
专题复习
二次函数——二次函数与相似的结合(1)
1、
教学目标
1.
对“二次函数”与“相似三角形”相关知识有进一步的理解和认识;
2.
结合实际问题的讨论与分析,培养观察、猜想以及运用所学的数学知识分析、解决实际问题的能力。
3、体会数形结合、分类讨论等数学思想,在小组合作交流学习中,有进一步的提高,增强解题信心。
1、
教学重点与难点
教学重点:利用“二次函数”和“相似三角形”相关知识解决综合问题
教学难点:结合分类讨论、数学结合等数学思想,解决综合问题
1、
教学过程
1.
开启记忆之门:
二次函数的相关知识
函数解析式
对称轴
顶点
开口方向
顶点式
直线
开口向上
开口向下
一般式
直线
开口向上
开口向下
2.
达标训练——动点在线段上
例:如图,平面直角坐标系中,已知,一次函数的图像与轴、轴分别交于点、两点,二次函数的图像经过点、点;
(1)求这个二次函数的解析式;
(2)点是该二次函数图像的顶点,求△的面积;
(3)如果点在线段上,且△与△相似,求点的坐标;
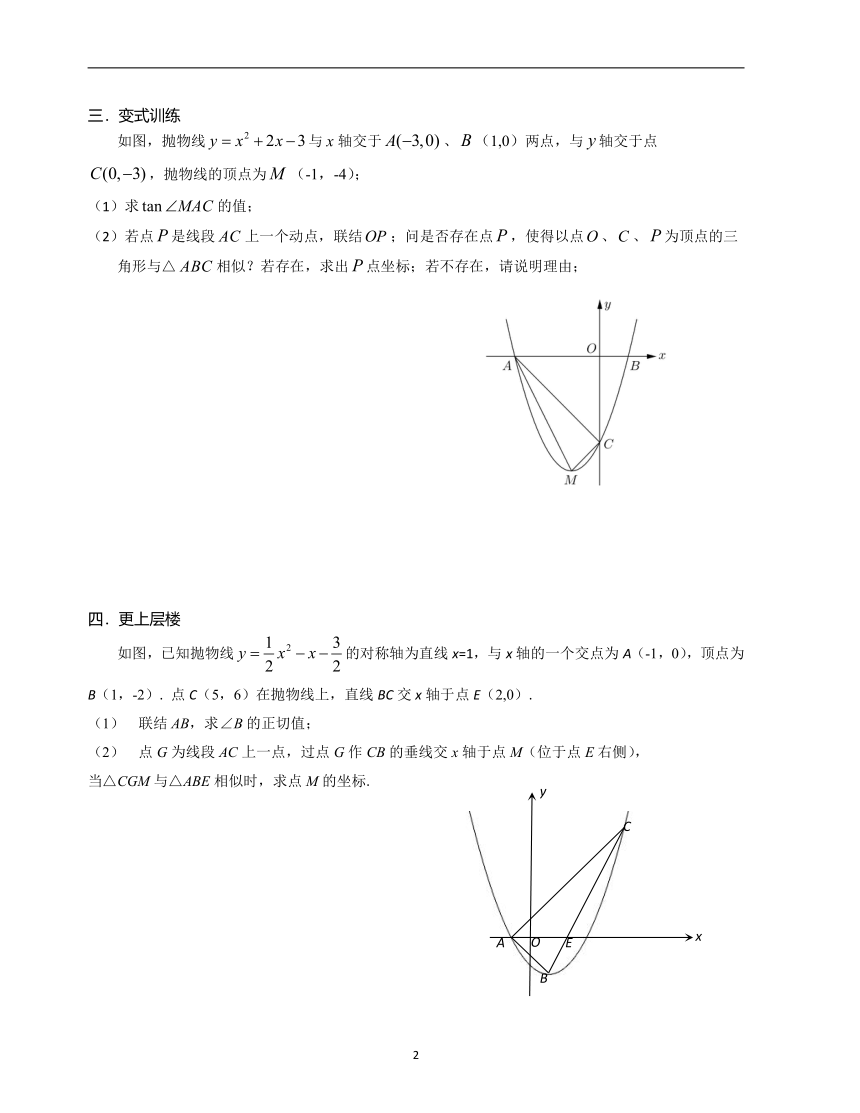
三.变式训练
如图,抛物线与轴交于、(1,0)两点,与轴交于点
,抛物线的顶点为(-1,-4);
(1)求的值;
(2)若点是线段上一个动点,联结;问是否存在点,使得以点、、为顶点的三角形与△相似?若存在,求出点坐标;若不存在,请说明理由;
四.更上层楼
如图,已知抛物线的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B(1,-2).
点C(5,6)在抛物线上,直线BC交x轴于点E(2,0).
(1)
联结AB,求∠B的正切值;
(2)
点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),
当△CGM与△ABE相似时,求点M的坐标.
五.归纳梳理
函数中因动点产生的相似三角形问题一般解题途径之一:
求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
6.布置作业
题型二:动点在线段的延长线上
如图7,已知抛物线与轴交于点和点(点在点的左侧),与轴交于点,且,点是抛物线的顶点,直线和交于点。
A层:(1)求点的坐标;
B层:(2)联结,求的余切值;
C层:(3)设点在线段延长线上,如果和相似,求点的坐标。
题型三:动点在对称轴上
如图,抛物线经过点,,为抛物线的顶点。
A层:(1)求抛物线的解析式及顶点坐标;
B层:(2)点关于抛物线的对称点为点,联结,,求的正切值;
C层:(3)点是抛物线对称轴上一点,且△和△相似,求点的坐标。
题型四:动点在某直线上
如图,已知抛物线经过的三个顶点,其中点,点,轴.
A层:(1)求这条抛物线的解析式;
B层:(2)求的值;
C层:(3)若点D为抛物线的顶点,点E是直线AC上一点,
当与相似时,求点E的坐标.
a<0
开口
向下
开口
向下
x
y
A
B
E
C
O
y
A
O
C
B
x
二次函数——二次函数与相似的结合(1)
1、
教学目标
1.
对“二次函数”与“相似三角形”相关知识有进一步的理解和认识;
2.
结合实际问题的讨论与分析,培养观察、猜想以及运用所学的数学知识分析、解决实际问题的能力。
3、体会数形结合、分类讨论等数学思想,在小组合作交流学习中,有进一步的提高,增强解题信心。
1、
教学重点与难点
教学重点:利用“二次函数”和“相似三角形”相关知识解决综合问题
教学难点:结合分类讨论、数学结合等数学思想,解决综合问题
1、
教学过程
1.
开启记忆之门:
二次函数的相关知识
函数解析式
对称轴
顶点
开口方向
顶点式
直线
开口向上
开口向下
一般式
直线
开口向上
开口向下
2.
达标训练——动点在线段上
例:如图,平面直角坐标系中,已知,一次函数的图像与轴、轴分别交于点、两点,二次函数的图像经过点、点;
(1)求这个二次函数的解析式;
(2)点是该二次函数图像的顶点,求△的面积;
(3)如果点在线段上,且△与△相似,求点的坐标;
三.变式训练
如图,抛物线与轴交于、(1,0)两点,与轴交于点
,抛物线的顶点为(-1,-4);
(1)求的值;
(2)若点是线段上一个动点,联结;问是否存在点,使得以点、、为顶点的三角形与△相似?若存在,求出点坐标;若不存在,请说明理由;
四.更上层楼
如图,已知抛物线的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B(1,-2).
点C(5,6)在抛物线上,直线BC交x轴于点E(2,0).
(1)
联结AB,求∠B的正切值;
(2)
点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),
当△CGM与△ABE相似时,求点M的坐标.
五.归纳梳理
函数中因动点产生的相似三角形问题一般解题途径之一:
求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
6.布置作业
题型二:动点在线段的延长线上
如图7,已知抛物线与轴交于点和点(点在点的左侧),与轴交于点,且,点是抛物线的顶点,直线和交于点。
A层:(1)求点的坐标;
B层:(2)联结,求的余切值;
C层:(3)设点在线段延长线上,如果和相似,求点的坐标。
题型三:动点在对称轴上
如图,抛物线经过点,,为抛物线的顶点。
A层:(1)求抛物线的解析式及顶点坐标;
B层:(2)点关于抛物线的对称点为点,联结,,求的正切值;
C层:(3)点是抛物线对称轴上一点,且△和△相似,求点的坐标。
题型四:动点在某直线上
如图,已知抛物线经过的三个顶点,其中点,点,轴.
A层:(1)求这条抛物线的解析式;
B层:(2)求的值;
C层:(3)若点D为抛物线的顶点,点E是直线AC上一点,
当与相似时,求点E的坐标.
a<0
开口
向下
开口
向下
x
y
A
B
E
C
O
y
A
O
C
B
x
