5.1.1 任意角(26张PPT)
文档属性
| 名称 | 5.1.1 任意角(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 18:21:42 | ||
图片预览






文档简介
(共26张PPT)
第五章
三角函数
5.1.1任意角
1.在初中角是如何定义的?
定义1:有公共端点的两条射线组成的几何图形叫做角。
顶点
边
边
【新课引入】
o
A
B
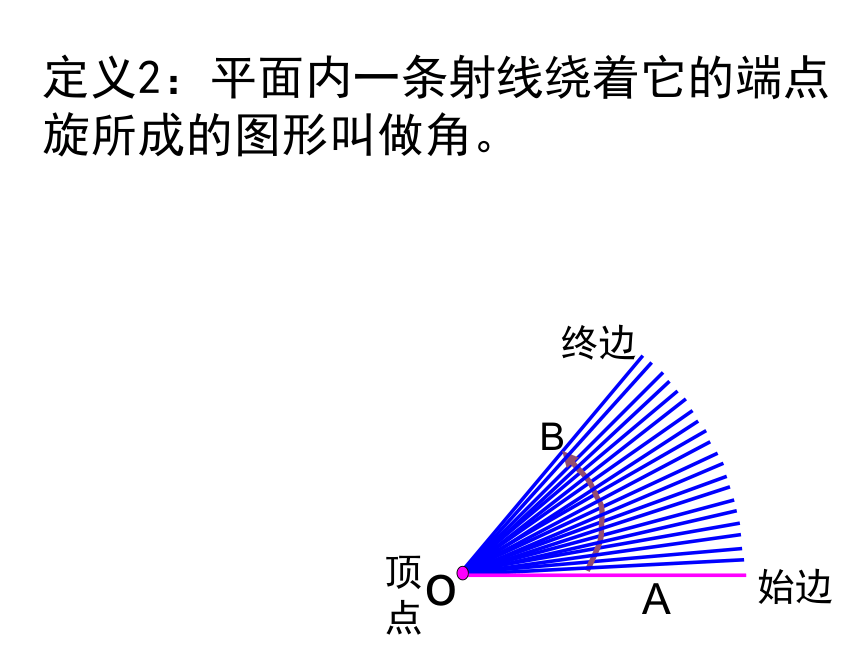
始边
终边
顶点
定义2:平面内一条射线绕着它的端点旋所成的图形叫做角。
2.过去我们学习了0°~360°范围的角,但在实际问题中还会遇到其他角.如在体操、花样滑冰、跳台跳水等比赛中,常常听到“转体10800”、“转体12600”这样的解说.再如钟表的指针、拧动螺丝的扳手、机器上的轮盘等,它们按照不同方向旋转所成的角,不全是0°~3600范围内的角.因此,仅有0°~360°范围内的角是不够的,我们必须将角的概念进行推广.
转体三周半指的是多少度?
这些例子所提到的角不仅不在范围[00
,3600
]
内,而且方向不同,这就需要将角的概念进行推广。想想用什么办法才能对角进行推广呢?
运
动
思考1:在齿轮传动中,被动轮与主动轮是按相反方向旋转的.我们将一条射线绕其端点按逆时针方向旋转600所形成的角,与按顺时针方向旋转600所形成的角是否相等?
知识探究(一):角的概念的推广
思考2:为了区分形成角的两种不同的旋转方向,可以作怎样的规定?如果一条射线没有作任何旋转,它还形成一个角吗?
规定:
按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.
如果一条射线没有作任何旋转,则称它形成了一个零角。即零角的始边和终边重合。
这样,就将角的概念推广到了
任意角:包括正角,负角和零角。
旋转方向相同且旋转量相等的两个角相等。
画图表示一个大小一定的角:
(1)画一条射线作为角的始边;
(2)由角的正负确定角的旋转方向;
(3)再由角的绝对值大小确定角的旋转量;
(4)画出角的终边,并用带箭头的螺旋线加以标注.
β
B2
γ
A
B1
α
O
思考3:度量一个角的大小,既要考虑旋转方向,
又要考虑旋转量,通过上述规定,角的范围
就扩展到了任意大小.
对于α=210°,
=-150°,
=-660°,你能用图形表
示这些角吗?你能总结一下作图的要点吗?
演示角
思考4:如果你的手表慢了20分钟,或快了1.25小时,你应该将分钟分别旋转多少度才能将时间校准?
思考5:任意两个角的数量大小可以相加、相
减,如50°+80°=130°,50°-80°=-30°,
你能解释一下这两个式子的几何意义吗?
以50°角的终边为始边,逆时针(或顺时针)旋转80°所成的角.
450°.
-120°,
角的加法和减法:
设α,β是任意两个角,
(1)α+β:把角α的终边旋转角β;
(2)α-β:α-β=α+(-β).
注:把射线OA绕端点O按不同的方向旋转相同的量所成的两个角叫做互为相反角,角α的相反角记为-α。
思考6:一个角的始边与终边可以重合吗?如果可以,这样的角的大小有什么特点?
k·360°(k∈Z)
演示
知识探究(二):象限角
思考1:为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意的角,角的终边可能落在哪些位置?
x
o
y
思考2:下列各角:-50°,405°,210°,
-200°,-450°分别是第几象限的角?
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
归纳:
在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么角的终边在第几象限,就说这个角是第几象限的角;
如果角的终边在坐标轴上,就认为这个角不属于任何一个象限。
思考3:锐角与第一象限的角是什么逻辑关系?钝角与第二象限的角是什么逻辑关系?直角与轴线角是什么逻辑关系?
思考4:第二象限的角一定比第一象限的角大吗?
象限角只能反映角的终边所在象限,不能反映角的大小.
思考5:在直角坐标系中,135°角的终边在什么位置?终边在该位置的角一定是135°吗?
x
y
o
知识探究(三):终边相同的角
思考1
390?
,?330?,30?
,1470?
,?1770?是第几象限的角?这些角的终边有什么关系?
x
y
o
300
它们都是第一象限的角,角的终边相同
-330o
390o
300
思考2:这些角与30°角在数量上相差多少?
。除了这些角而外还有哪些角与30°角终边相同?
相差360o的整数倍
2×360o+30o
-2×360o+30o
3×360o+30o
-3×360o+30o
4×360o+30o
-4×360o+30o
……,
……,
390°=30°+1×360°
-330°=30°+(-1)×360°
1470°=30°+4×360°
-1770°=30°+(-5)×360°
思考3:所有与30°角终边相同的角,连同-30°角在内,可构成一个集合S,
你能用描述法表示集合S吗?
S={β|β=α+k·360°,k∈Z},
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
思考4:一般地,所有与角α终边相同的角,
连同角α在内所构成的集合S可以怎样表示?
S={β|β=
30°
+k·360°, k∈Z}
S={β|β=α+k·360°,k∈Z}
注意:
⑴
k∈Z
⑵
α是任一角;
⑶
终边相同的角不一定相等,但相等的角终边一定相同.终边相同的角有无限个,它们相差360°的整数倍。
理论迁移
例1
在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
解:-950°12′=129°48′-360°×
3
所以,在0°~360°范围内,与-950°12′角终边相同的角是129°48′,它是第二象限角.
理论迁移
S=S1US2
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°k∈Z}∪{β|β=90°+(2k+1)180°k∈Z}
={β|β=90°+n·180°,n∈Z}.
例2
写出终边在y轴上的角的集合.
解:在0°~360”范围内,终边在y轴上的角有两个,
即90°,270°角(图5.1-7)。
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z},
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z},
于是,终边在y轴上的角的集合
理论迁移
S中适合不等式一360°≤β<720°的元素β有
45°-2×180°=-315°,
45°-1×180°=—135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
例3
写出终边在直线y=x上的角的集合S.S中满足不等式
一360°≤β<720”的元素β有哪些?
解:如图5.1-8,在直角坐标系中画出直线y=x,可以发现它与x轴的夹角是45°,在0~360范围内,终边在直线y=x上的角有两个:45°,225°.
因此,终边在直线y=x上的角的集合
S={β|β=45°+k·360°,k∈Z}∪
{β|β=225°+k·360°,k∈Z}
={β|β=45°+n·180°,n∈Z}.
小结
1、角的定义
2、任意角的概念
正角:射线按逆时针方向旋转形成的角
负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
3、象限角
1)置角的顶点于原点
2)始边重合于X轴的非负半轴
3)终边落在第几象限就是第几象限角
4、
终边与
角α相同的角
第五章
三角函数
5.1.1任意角
1.在初中角是如何定义的?
定义1:有公共端点的两条射线组成的几何图形叫做角。
顶点
边
边
【新课引入】
o
A
B
始边
终边
顶点
定义2:平面内一条射线绕着它的端点旋所成的图形叫做角。
2.过去我们学习了0°~360°范围的角,但在实际问题中还会遇到其他角.如在体操、花样滑冰、跳台跳水等比赛中,常常听到“转体10800”、“转体12600”这样的解说.再如钟表的指针、拧动螺丝的扳手、机器上的轮盘等,它们按照不同方向旋转所成的角,不全是0°~3600范围内的角.因此,仅有0°~360°范围内的角是不够的,我们必须将角的概念进行推广.
转体三周半指的是多少度?
这些例子所提到的角不仅不在范围[00
,3600
]
内,而且方向不同,这就需要将角的概念进行推广。想想用什么办法才能对角进行推广呢?
运
动
思考1:在齿轮传动中,被动轮与主动轮是按相反方向旋转的.我们将一条射线绕其端点按逆时针方向旋转600所形成的角,与按顺时针方向旋转600所形成的角是否相等?
知识探究(一):角的概念的推广
思考2:为了区分形成角的两种不同的旋转方向,可以作怎样的规定?如果一条射线没有作任何旋转,它还形成一个角吗?
规定:
按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.
如果一条射线没有作任何旋转,则称它形成了一个零角。即零角的始边和终边重合。
这样,就将角的概念推广到了
任意角:包括正角,负角和零角。
旋转方向相同且旋转量相等的两个角相等。
画图表示一个大小一定的角:
(1)画一条射线作为角的始边;
(2)由角的正负确定角的旋转方向;
(3)再由角的绝对值大小确定角的旋转量;
(4)画出角的终边,并用带箭头的螺旋线加以标注.
β
B2
γ
A
B1
α
O
思考3:度量一个角的大小,既要考虑旋转方向,
又要考虑旋转量,通过上述规定,角的范围
就扩展到了任意大小.
对于α=210°,
=-150°,
=-660°,你能用图形表
示这些角吗?你能总结一下作图的要点吗?
演示角
思考4:如果你的手表慢了20分钟,或快了1.25小时,你应该将分钟分别旋转多少度才能将时间校准?
思考5:任意两个角的数量大小可以相加、相
减,如50°+80°=130°,50°-80°=-30°,
你能解释一下这两个式子的几何意义吗?
以50°角的终边为始边,逆时针(或顺时针)旋转80°所成的角.
450°.
-120°,
角的加法和减法:
设α,β是任意两个角,
(1)α+β:把角α的终边旋转角β;
(2)α-β:α-β=α+(-β).
注:把射线OA绕端点O按不同的方向旋转相同的量所成的两个角叫做互为相反角,角α的相反角记为-α。
思考6:一个角的始边与终边可以重合吗?如果可以,这样的角的大小有什么特点?
k·360°(k∈Z)
演示
知识探究(二):象限角
思考1:为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意的角,角的终边可能落在哪些位置?
x
o
y
思考2:下列各角:-50°,405°,210°,
-200°,-450°分别是第几象限的角?
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
归纳:
在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么角的终边在第几象限,就说这个角是第几象限的角;
如果角的终边在坐标轴上,就认为这个角不属于任何一个象限。
思考3:锐角与第一象限的角是什么逻辑关系?钝角与第二象限的角是什么逻辑关系?直角与轴线角是什么逻辑关系?
思考4:第二象限的角一定比第一象限的角大吗?
象限角只能反映角的终边所在象限,不能反映角的大小.
思考5:在直角坐标系中,135°角的终边在什么位置?终边在该位置的角一定是135°吗?
x
y
o
知识探究(三):终边相同的角
思考1
390?
,?330?,30?
,1470?
,?1770?是第几象限的角?这些角的终边有什么关系?
x
y
o
300
它们都是第一象限的角,角的终边相同
-330o
390o
300
思考2:这些角与30°角在数量上相差多少?
。除了这些角而外还有哪些角与30°角终边相同?
相差360o的整数倍
2×360o+30o
-2×360o+30o
3×360o+30o
-3×360o+30o
4×360o+30o
-4×360o+30o
……,
……,
390°=30°+1×360°
-330°=30°+(-1)×360°
1470°=30°+4×360°
-1770°=30°+(-5)×360°
思考3:所有与30°角终边相同的角,连同-30°角在内,可构成一个集合S,
你能用描述法表示集合S吗?
S={β|β=α+k·360°,k∈Z},
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
思考4:一般地,所有与角α终边相同的角,
连同角α在内所构成的集合S可以怎样表示?
S={β|β=
30°
+k·360°, k∈Z}
S={β|β=α+k·360°,k∈Z}
注意:
⑴
k∈Z
⑵
α是任一角;
⑶
终边相同的角不一定相等,但相等的角终边一定相同.终边相同的角有无限个,它们相差360°的整数倍。
理论迁移
例1
在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
解:-950°12′=129°48′-360°×
3
所以,在0°~360°范围内,与-950°12′角终边相同的角是129°48′,它是第二象限角.
理论迁移
S=S1US2
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°k∈Z}∪{β|β=90°+(2k+1)180°k∈Z}
={β|β=90°+n·180°,n∈Z}.
例2
写出终边在y轴上的角的集合.
解:在0°~360”范围内,终边在y轴上的角有两个,
即90°,270°角(图5.1-7)。
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z},
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z},
于是,终边在y轴上的角的集合
理论迁移
S中适合不等式一360°≤β<720°的元素β有
45°-2×180°=-315°,
45°-1×180°=—135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
例3
写出终边在直线y=x上的角的集合S.S中满足不等式
一360°≤β<720”的元素β有哪些?
解:如图5.1-8,在直角坐标系中画出直线y=x,可以发现它与x轴的夹角是45°,在0~360范围内,终边在直线y=x上的角有两个:45°,225°.
因此,终边在直线y=x上的角的集合
S={β|β=45°+k·360°,k∈Z}∪
{β|β=225°+k·360°,k∈Z}
={β|β=45°+n·180°,n∈Z}.
小结
1、角的定义
2、任意角的概念
正角:射线按逆时针方向旋转形成的角
负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
3、象限角
1)置角的顶点于原点
2)始边重合于X轴的非负半轴
3)终边落在第几象限就是第几象限角
4、
终边与
角α相同的角
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
