人教版数学八年级上册12.2三角形全等的判定-ASA、AAS 教学设计(表格式)
文档属性
| 名称 | 人教版数学八年级上册12.2三角形全等的判定-ASA、AAS 教学设计(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 70.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 18:28:33 | ||
图片预览


文档简介
课程基本信息
课题
三角形全等的判定——ASA、AAS
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:
2013
年
6月
教学目标
教学目标:1.探索并掌握“ASA”和“AAS”判定方法;
2.会用“ASA”和“AAS”判定方法证明两个三角形全等;
3.经历猜想,作图验证,逻辑推理的几何探究过程,发展问题分析能力和几何表述能力.
教学重点:用“ASA”和“AAS”判定方法证明两个三角形全等,并能进行简单的应用.
教学难点:1.
“AAS”判定方法的证明.
2.用“ASA”和“AAS”判定方法证明两个三角形全等.
教学过程
时间
教学环节
主要师生活动
2分钟
复习巩固,引发思考
复习:我们已经学习了哪些判定两个三角形全等的方法,它们分别需要哪些条件呢?
思考:将条件替换为两组对应角相等,一组对应边相等后,是否能判定两个三角形全等呢?
注:相等的边可能为两角的夹边,也可能为其中一角所对的边,应进行分类讨论.
8分钟
条件探索,作图归纳
探究1:先在一张纸上画一个△ABC,然后在另一张纸上画△A′B′C′,使A′B′
=AB,∠A′=∠A,∠B′=∠B.△A′B′C′和△ABC能重合吗?根据你画的两个三角形及结果,你能得到又一个判定两个三角形全等的方法吗?
作法:(1)
画A′B′=AB;
(2)在A′B′的同旁画∠DA′B=∠A,
∠EB′A=∠B,A′D、B′E
相交于点C′.
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
归纳概括“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等(简称为“角边角”或“ASA”).
几何语言:在△ABC
与△A′B′C′中,
∴ △ABC
≌△A′B′C′
(ASA)
探究2:如果△ABC和△A′B′C′满足,使B′C
′=BC,∠A′=∠A,∠B′=∠B.△A′B′C′
和△ABC是全等的吗?
【思路】利用三角形的内角和,转化为“ASA”进行证明.
【结论】两角和其中一角的对边分别相等的两个三角形全等(简称为“角角边”或“AAS”).
几何语言:在△ABC
与△A′B′C′中,
∴ △ABC
≌△A′B′C′
(AAS)
13分钟
知识应用
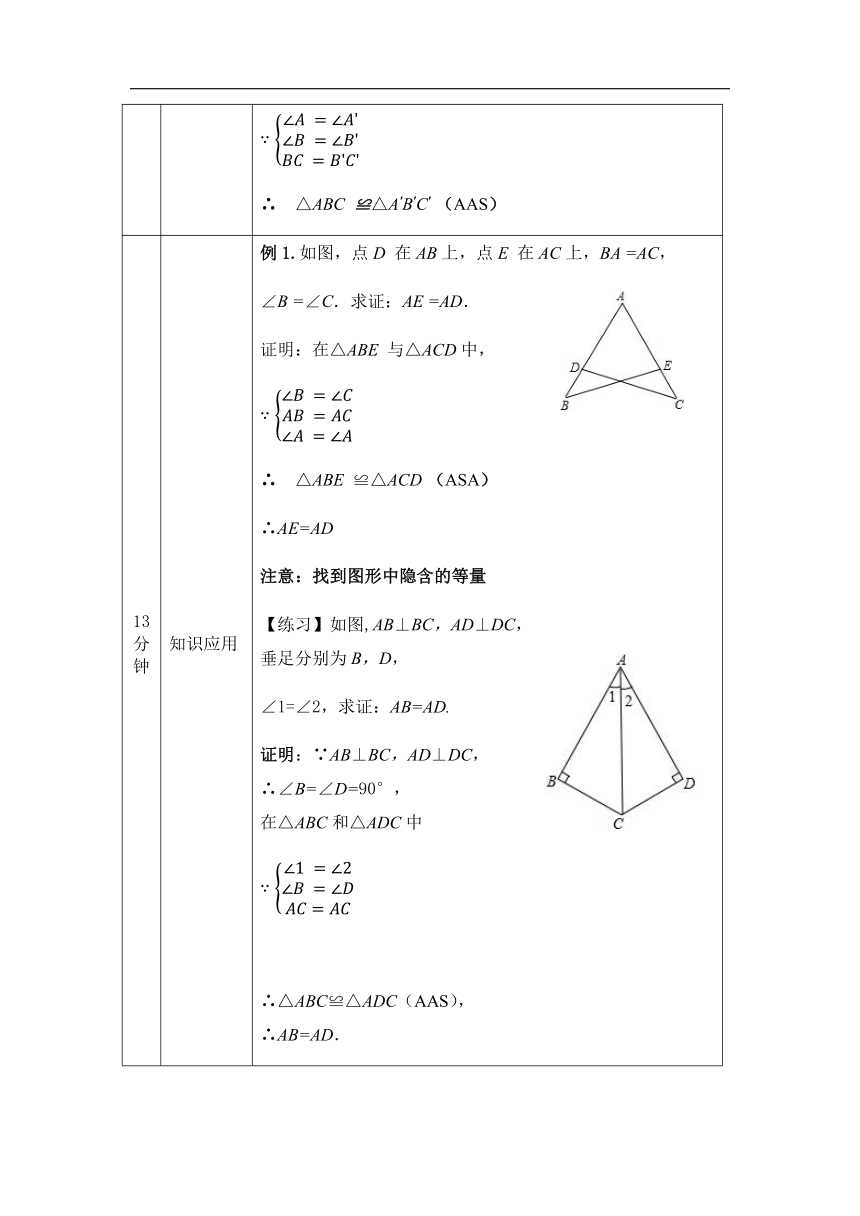
例1.如图,点D
在AB上,点E
在AC上,BA
=AC,
∠B
=∠C.求证:AE
=AD.
证明:在△ABE
与△ACD中,
∴ △ABE
≌△ACD
(ASA)
∴AE=AD
注意:找到图形中隐含的等量
【练习】如图,AB⊥BC,AD⊥DC,垂足分别为B,D,
∠1=∠2,求证:AB=AD.
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在△ABC和△ADC中
∴△ABC≌△ADC(AAS),
∴AB=AD.
例2.如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长度就是AB的长,为什么?
解:∵AB⊥BF,DE⊥BF
∴∠B=∠CDE=90°
在△ABC和△EDC中
∴△ABC≌△EDC(ASA),
∴AB=DE.
例3.
如图,AE⊥BE,AD⊥DC,CD
=BE,∠DAB=∠EAC.求证:AB
=AC.
证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠EAB
∵AE⊥BE,AD⊥DC
∴∠D=∠E=90°
在△ACD和△ABE中,
∴△ACD≌△EAB(AAS),
∴AB=AC.
注意:利用等式的性质,构造全等所需的等量.
【练习】如图,已知∠1=∠2,∠B=∠D,
求证:△ABC≌△ADC.
证:∵∠ACB+∠1
=180°,
∠ACD+∠2=180°,
∠1=∠2
∴ ∠ACB=∠ACD
在△ABC与△ADC中,
∴△ABC≌△ADC(AAS)
思考:本题还有其他方法吗?
另证:∵∠1
是△ABC的外角,∠2
是△ADC的外角
∴∠BAC+∠B=∠1,∠DAC+∠D=∠2
∵∠B=∠D,∠1=∠2
∴∠BAC=∠DAC
在△ABC与△ADC中,
∴△ABC≌△ADC(AAS)
2分钟
课堂小结
本节课学习了几种判断两个三角形全等的方法?分别是什么?它们之间有什么共同点和区别?
ASA——两角和它们的夹边分别相等的两个三角形全等.
AAS——两角和其中一角的对边分别相等的两个三角形全等.
共同点:都要求两角和一边相等.
区别:ASA——夹边
AAS——对边.
由上述两个判定我们发现,当两个三角形有两个角对应相等后,相等的那条边可以为三边中的任意边。因此,我们可以归纳为“若两角一边相等,则三角形全等”
来代替?
在证明三角形全等的过程中,往往需要我们构造所需条件,此时需注意:
①挖掘图形中的隐含条件:公共角、公共边、对顶角;
②利用等式性质或几何知识转化条件.
课后作业
1.
如图,∠1=∠2,∠B=∠D,求证:AB=CD.
2.如图,∠ACB=90°,AC=CB,AD⊥CE,BE⊥CE,垂足分别为D,E.
求证:△ACD≌△CBE.
3.如图,A,B两点被池塘隔开,某同学用以下方法测得池塘的宽度AB:过点B作BC⊥AB,作∠BCD=∠BCA,使A,B,D三点在一条直线上,则测量出BD的长即为AB的长,这是为什么呢?
课题
三角形全等的判定——ASA、AAS
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:
2013
年
6月
教学目标
教学目标:1.探索并掌握“ASA”和“AAS”判定方法;
2.会用“ASA”和“AAS”判定方法证明两个三角形全等;
3.经历猜想,作图验证,逻辑推理的几何探究过程,发展问题分析能力和几何表述能力.
教学重点:用“ASA”和“AAS”判定方法证明两个三角形全等,并能进行简单的应用.
教学难点:1.
“AAS”判定方法的证明.
2.用“ASA”和“AAS”判定方法证明两个三角形全等.
教学过程
时间
教学环节
主要师生活动
2分钟
复习巩固,引发思考
复习:我们已经学习了哪些判定两个三角形全等的方法,它们分别需要哪些条件呢?
思考:将条件替换为两组对应角相等,一组对应边相等后,是否能判定两个三角形全等呢?
注:相等的边可能为两角的夹边,也可能为其中一角所对的边,应进行分类讨论.
8分钟
条件探索,作图归纳
探究1:先在一张纸上画一个△ABC,然后在另一张纸上画△A′B′C′,使A′B′
=AB,∠A′=∠A,∠B′=∠B.△A′B′C′和△ABC能重合吗?根据你画的两个三角形及结果,你能得到又一个判定两个三角形全等的方法吗?
作法:(1)
画A′B′=AB;
(2)在A′B′的同旁画∠DA′B=∠A,
∠EB′A=∠B,A′D、B′E
相交于点C′.
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
归纳概括“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等(简称为“角边角”或“ASA”).
几何语言:在△ABC
与△A′B′C′中,
∴ △ABC
≌△A′B′C′
(ASA)
探究2:如果△ABC和△A′B′C′满足,使B′C
′=BC,∠A′=∠A,∠B′=∠B.△A′B′C′
和△ABC是全等的吗?
【思路】利用三角形的内角和,转化为“ASA”进行证明.
【结论】两角和其中一角的对边分别相等的两个三角形全等(简称为“角角边”或“AAS”).
几何语言:在△ABC
与△A′B′C′中,
∴ △ABC
≌△A′B′C′
(AAS)
13分钟
知识应用
例1.如图,点D
在AB上,点E
在AC上,BA
=AC,
∠B
=∠C.求证:AE
=AD.
证明:在△ABE
与△ACD中,
∴ △ABE
≌△ACD
(ASA)
∴AE=AD
注意:找到图形中隐含的等量
【练习】如图,AB⊥BC,AD⊥DC,垂足分别为B,D,
∠1=∠2,求证:AB=AD.
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在△ABC和△ADC中
∴△ABC≌△ADC(AAS),
∴AB=AD.
例2.如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长度就是AB的长,为什么?
解:∵AB⊥BF,DE⊥BF
∴∠B=∠CDE=90°
在△ABC和△EDC中
∴△ABC≌△EDC(ASA),
∴AB=DE.
例3.
如图,AE⊥BE,AD⊥DC,CD
=BE,∠DAB=∠EAC.求证:AB
=AC.
证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠EAB
∵AE⊥BE,AD⊥DC
∴∠D=∠E=90°
在△ACD和△ABE中,
∴△ACD≌△EAB(AAS),
∴AB=AC.
注意:利用等式的性质,构造全等所需的等量.
【练习】如图,已知∠1=∠2,∠B=∠D,
求证:△ABC≌△ADC.
证:∵∠ACB+∠1
=180°,
∠ACD+∠2=180°,
∠1=∠2
∴ ∠ACB=∠ACD
在△ABC与△ADC中,
∴△ABC≌△ADC(AAS)
思考:本题还有其他方法吗?
另证:∵∠1
是△ABC的外角,∠2
是△ADC的外角
∴∠BAC+∠B=∠1,∠DAC+∠D=∠2
∵∠B=∠D,∠1=∠2
∴∠BAC=∠DAC
在△ABC与△ADC中,
∴△ABC≌△ADC(AAS)
2分钟
课堂小结
本节课学习了几种判断两个三角形全等的方法?分别是什么?它们之间有什么共同点和区别?
ASA——两角和它们的夹边分别相等的两个三角形全等.
AAS——两角和其中一角的对边分别相等的两个三角形全等.
共同点:都要求两角和一边相等.
区别:ASA——夹边
AAS——对边.
由上述两个判定我们发现,当两个三角形有两个角对应相等后,相等的那条边可以为三边中的任意边。因此,我们可以归纳为“若两角一边相等,则三角形全等”
来代替?
在证明三角形全等的过程中,往往需要我们构造所需条件,此时需注意:
①挖掘图形中的隐含条件:公共角、公共边、对顶角;
②利用等式性质或几何知识转化条件.
课后作业
1.
如图,∠1=∠2,∠B=∠D,求证:AB=CD.
2.如图,∠ACB=90°,AC=CB,AD⊥CE,BE⊥CE,垂足分别为D,E.
求证:△ACD≌△CBE.
3.如图,A,B两点被池塘隔开,某同学用以下方法测得池塘的宽度AB:过点B作BC⊥AB,作∠BCD=∠BCA,使A,B,D三点在一条直线上,则测量出BD的长即为AB的长,这是为什么呢?
