沪教版(上海)初中数学七年级第一学期 9.7 同底数幂的乘法 课件 (1)(27张PPT)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.7 同底数幂的乘法 课件 (1)(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:21:32 | ||
图片预览





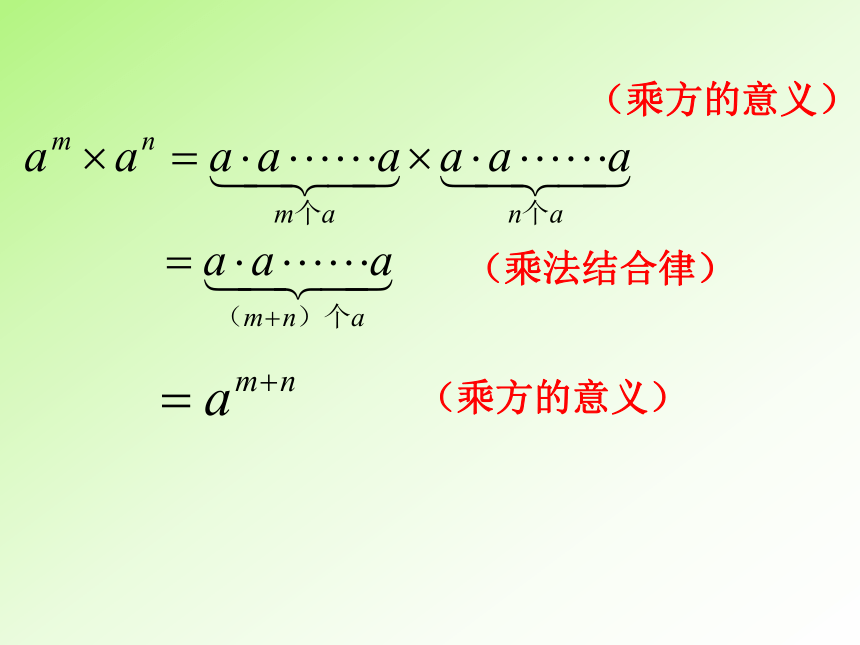
文档简介
七年级第一学期数学
9.7
同底数幂的乘法
若正方体的棱长为2,则其体积为多少?
2
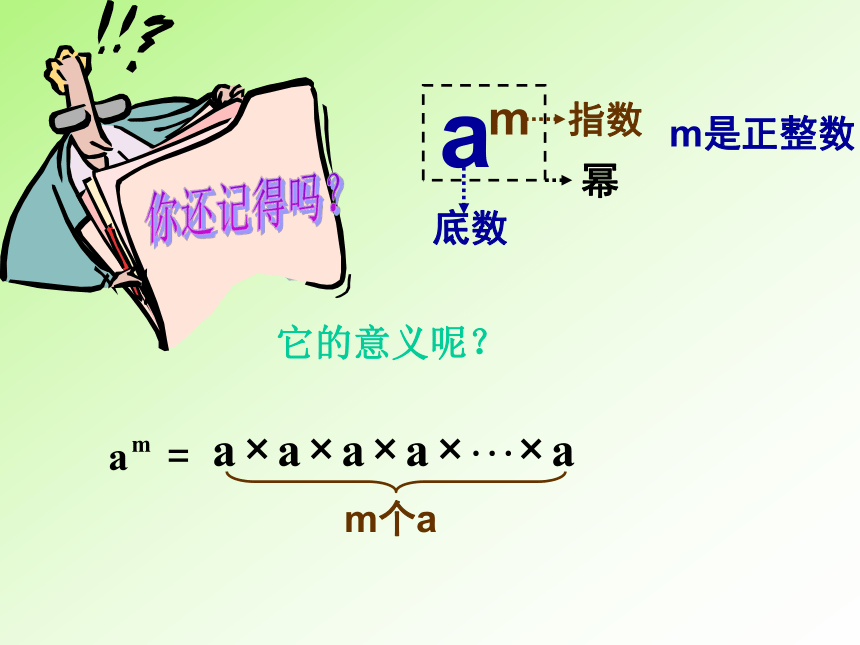
a
m
底数
指数
幂
m是正整数
它的意义呢?
m个a
把下列各式写成幂的形式:
(1)
(2)
(4)
(3)
* 负数与分数作底数时要打上括号。
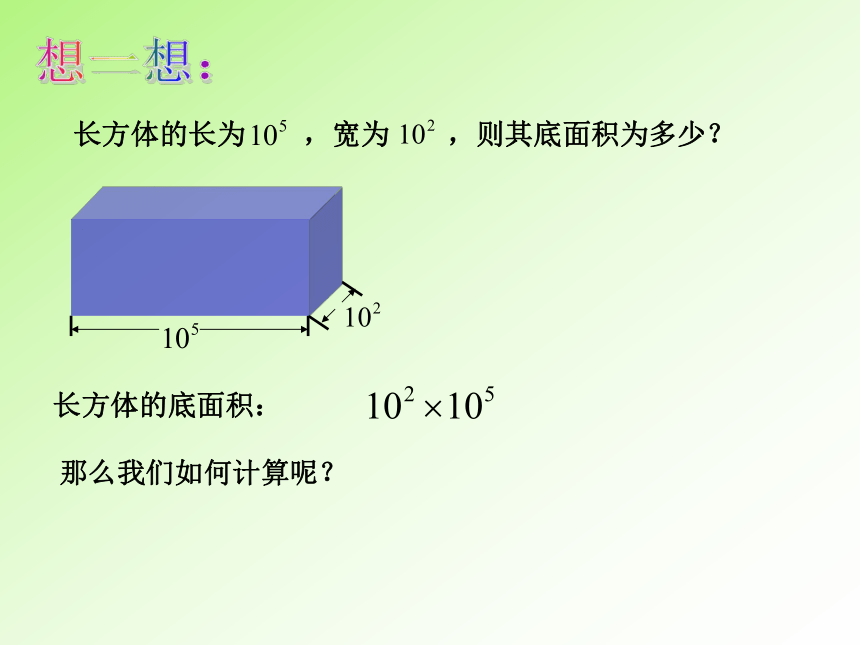
长方体的长为 ,宽为 ,则其底面积为多少?
长方体的底面积:
那么我们如何计算呢?
根据乘方的意义:
2个10
5个10
7个10
从而可得:
以2为底的幂
(1)
×
(2)
×
(3)
×
猜一猜:
×
7
8
6
m+n
以2为底的幂
我们观察上述各等式可以 发现,等式左边 的这两个因数底数相同,是同底的幂的形式
所以我们上述这种运算叫做
同底数幂的乘法
我们如何说明这个等式是否成立呢?请试一试
同底数幂的乘法
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,底数不变,指数相加
由此,我们可以得到:
(m、n是正整数)
长方体的长为 ,宽为 ,则其底面积为多少?
如果知道了这个长方体的高为 ,那么它的体积呢?
( )
如果有多个同底数幂相乘,底数仍不变,指数仍相加
(m、n、p是正整数)
练习一
1.???计算下列各式,结果用幂的形式表示
(2)
(3) (x+y)5 ·(y+x)6
(4) (a-b)4 ·(b-a)3
(1) 105×106
(5) (-a)3 ·(-a2)·a4· a
(6) (2m-n)2t+1 ·(n-2m)4t+2· (2m-n)
练习二
2、下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 · y5 =y10
c · c3 = c4
×
×
×
×
×
×
例1 计算:
(1)
(2)
(3)
(4)
(5)y4·y3·y2·y
例2 计算:
(1)
(2)
(3)
例3 计算:
(1)?????? x5·x3 – x4·x4 + x7·x + x6x2
(2)?????? y2·ym–2 + y·ym–1 – y3·ym
解:(1)原式 = x8 – x8 + x8 + x8 = 2x8
(2)原式 = ym + ym – ym+3 = 2ym – ym+3
1、填空:
(1)x5 ·( )= x 8 (2)a ·( )= -a6
(3)x · x3( )= x7 (4)xm ·( )=x3m
x3
(-a)5
x3
x2m
2、填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
练习三
3.???计算:
∵am · an = am+n (m、n为正整数)
∴ am+n = am · an (m、n为正整数)
已知:am=2, an=3.
求am+n =?.
动脑筋
解: am+n = am · an
=2 × 3=6
若已知 , 求 的值.
解一:
解二:由题意得 x + 3 = 5,解得x = 2
拓展训练,深化提高
填空:
(1)如果an–3·a2n+1 = a10,
则 n = ____________________;
(2)已知 2×8n×16n = 222,
则 n = ______________________;
(3) an+1·am+n = a6且m – 2n = 1,
则 mn = ______________________。
3
3
4
例4 已知 (x + y)2 = 2,(x - y)3 = 3
求:(x + y)7 (x - y)2 (y + x)3 (y - x)4
解:原式 =(x + y)7 (x - y)2 (x + y)3 (x - y)4
=(x + y)10 (x - y)6
=[(x + y)2]5 [(x - y)3]2
当(x + y)2=2,(x - y)3=3时
原式 =25 ×32 =288
am+n = am · an (m、n为正整数)
am · an = am+n (m、n为正整数)
* 公式中的a可以是数也可以是式子;
* 公式中的指数可以增加,法则仍然成立;
* – a2与(– a)2的区别;
* 底数互为相反数的可先化成同底数幂再计算;
(– a)2n = a2n;(x + y)n=(y +x)n
(– a)2n+1 = – a2n+1 ; (x – y)2n-1 = –(y – x)2n-1
* 同底数幂乘法法则可以逆用。
1、作业纸
2、预习9.8
9.7
同底数幂的乘法
若正方体的棱长为2,则其体积为多少?
2
a
m
底数
指数
幂
m是正整数
它的意义呢?
m个a
把下列各式写成幂的形式:
(1)
(2)
(4)
(3)
* 负数与分数作底数时要打上括号。
长方体的长为 ,宽为 ,则其底面积为多少?
长方体的底面积:
那么我们如何计算呢?
根据乘方的意义:
2个10
5个10
7个10
从而可得:
以2为底的幂
(1)
×
(2)
×
(3)
×
猜一猜:
×
7
8
6
m+n
以2为底的幂
我们观察上述各等式可以 发现,等式左边 的这两个因数底数相同,是同底的幂的形式
所以我们上述这种运算叫做
同底数幂的乘法
我们如何说明这个等式是否成立呢?请试一试
同底数幂的乘法
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,底数不变,指数相加
由此,我们可以得到:
(m、n是正整数)
长方体的长为 ,宽为 ,则其底面积为多少?
如果知道了这个长方体的高为 ,那么它的体积呢?
( )
如果有多个同底数幂相乘,底数仍不变,指数仍相加
(m、n、p是正整数)
练习一
1.???计算下列各式,结果用幂的形式表示
(2)
(3) (x+y)5 ·(y+x)6
(4) (a-b)4 ·(b-a)3
(1) 105×106
(5) (-a)3 ·(-a2)·a4· a
(6) (2m-n)2t+1 ·(n-2m)4t+2· (2m-n)
练习二
2、下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 · y5 =y10
c · c3 = c4
×
×
×
×
×
×
例1 计算:
(1)
(2)
(3)
(4)
(5)y4·y3·y2·y
例2 计算:
(1)
(2)
(3)
例3 计算:
(1)?????? x5·x3 – x4·x4 + x7·x + x6x2
(2)?????? y2·ym–2 + y·ym–1 – y3·ym
解:(1)原式 = x8 – x8 + x8 + x8 = 2x8
(2)原式 = ym + ym – ym+3 = 2ym – ym+3
1、填空:
(1)x5 ·( )= x 8 (2)a ·( )= -a6
(3)x · x3( )= x7 (4)xm ·( )=x3m
x3
(-a)5
x3
x2m
2、填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
练习三
3.???计算:
∵am · an = am+n (m、n为正整数)
∴ am+n = am · an (m、n为正整数)
已知:am=2, an=3.
求am+n =?.
动脑筋
解: am+n = am · an
=2 × 3=6
若已知 , 求 的值.
解一:
解二:由题意得 x + 3 = 5,解得x = 2
拓展训练,深化提高
填空:
(1)如果an–3·a2n+1 = a10,
则 n = ____________________;
(2)已知 2×8n×16n = 222,
则 n = ______________________;
(3) an+1·am+n = a6且m – 2n = 1,
则 mn = ______________________。
3
3
4
例4 已知 (x + y)2 = 2,(x - y)3 = 3
求:(x + y)7 (x - y)2 (y + x)3 (y - x)4
解:原式 =(x + y)7 (x - y)2 (x + y)3 (x - y)4
=(x + y)10 (x - y)6
=[(x + y)2]5 [(x - y)3]2
当(x + y)2=2,(x - y)3=3时
原式 =25 ×32 =288
am+n = am · an (m、n为正整数)
am · an = am+n (m、n为正整数)
* 公式中的a可以是数也可以是式子;
* 公式中的指数可以增加,法则仍然成立;
* – a2与(– a)2的区别;
* 底数互为相反数的可先化成同底数幂再计算;
(– a)2n = a2n;(x + y)n=(y +x)n
(– a)2n+1 = – a2n+1 ; (x – y)2n-1 = –(y – x)2n-1
* 同底数幂乘法法则可以逆用。
1、作业纸
2、预习9.8
