沪教版(上海)初中数学七年级第一学期 9.7 同底数幂的乘法 课件(32张PPT)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.7 同底数幂的乘法 课件(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:08:47 | ||
图片预览

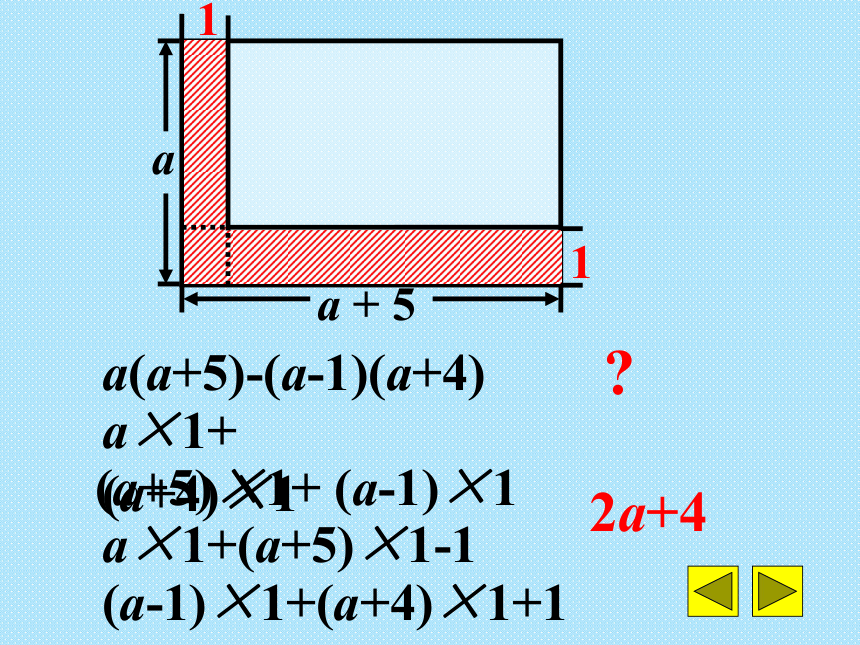








文档简介
9.7
同底数幂的乘法
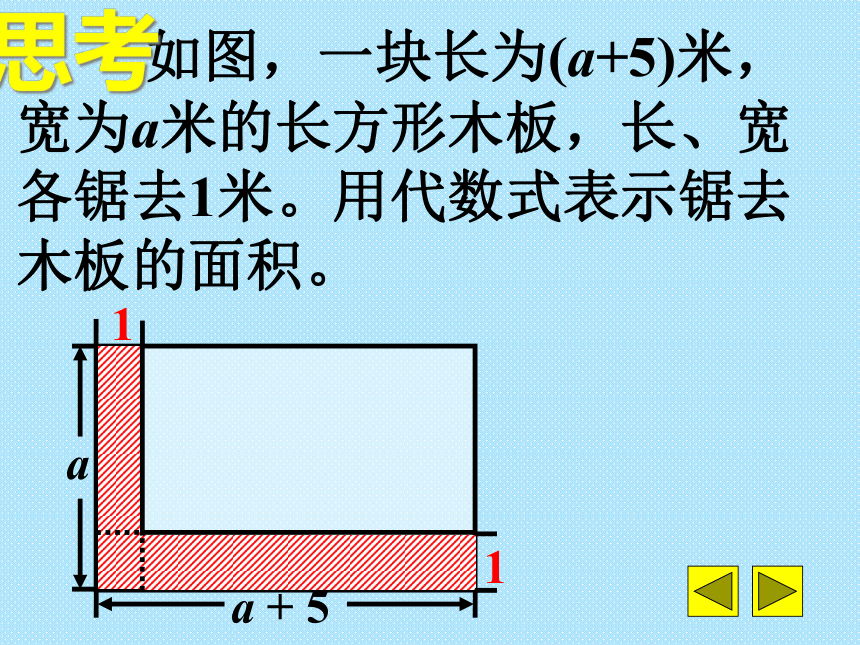
如图,一块长为(a+5)米,宽为a米的长方形木板,长、宽各锯去1米。用代数式表示锯去木板的面积。
思考
a
1
1
a + 5
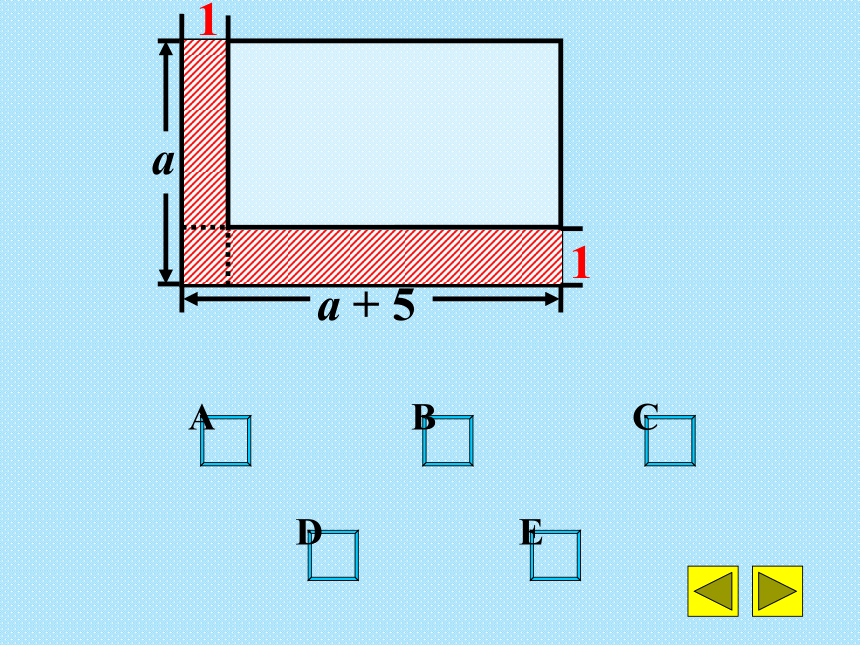
A
E
B
C
D
a
1
1
a + 5
a×1+ (a+4)×1
(a+5)×1+ (a-1)×1
a×1+(a+5)×1-1
(a-1)×1+(a+4)×1+1
a(a+5)-(a-1)(a+4)
2a+4
?
a
1
1
a + 5
课前练习
式子103,a5各表示什么意思?
103表示3个10连乘;
a5表示5个a连乘。
课前练习
指出下列各式子的底数和指数,并计算其结果。
32
(-3)2
-52
-34
3
3
2
4
=9
=9
=
=
=-25
=-81
=
=-
课前练习
化简:
(-a)4
(-a)5
=a4
= -a5
课前练习
合并下列各题中的同类项:
(1)3a3+ 2a3
(2)3a3- 3a2- a3
=5a3
=2a3 - 3a2
试一试 计算3a3? 2a3
2a3?(-3a2)
观察
下列四小题中的两个幂有什么共同之处?
(3)a3? a3;
(4)a3? a2。
(1)103×102;
(2)24×23;
10
10
2
2
a
a
a
a
同底数幂的乘法
(3)a3? a3;
(4)a3? a2。
(1)103×102;
(2)24×23;
10
10
2
2
a
a
a
a
试一试
计算下列四小题
(3)a3? a3;
(4)a3? a2。
(1)103×102;
(2)24×23;
10
10
2
2
a
a
a
a
(3)a3? a3 = a6 ;
(4)a3? a2 = a5 ,
由(1)103×102= 105 ;
(2)24×23 = 27 ;
猜想
am ? an=
(m,n都是正整数)
你能说明你的猜想的正确性吗?
am+n
从左到右的变化。
am ? an
(其中m,n都是正整数)
= a( )
= (a?a? ?a) ? (a?a? ?a)
( )个
m+n
m
n
m+n
…
…
= a? a? ? a
…
( )个
( )个
am ? an= am+n
(m,n都是正整数)
你能用自己的语言概括同底数幂相乘的运算法则吗?
am ? an= am+n
(m,n都是正整数)
同底数幂相乘的性质:
同底数幂相乘, 不变, 相加。
底数
指数
am ? an ? ap=
(m,n,p都是正整数)
am+n+p
例1.计算:
(1)107×104 ;
(2)
3 ;
?
(3) x2 ? x5 ;
(5) y ? y2 ? y3 。
(4)23×24×25 ;
例1.计算:
解:(1)107×104
(2)
3
?
=107+4
=1011
= 1+3
= 4
=
例1.计算:
(3) x2 ? x5
(5) y ? y2 ? y3
(4)23×24×25
=x2+5
=x7
=y1+2+3
=y6
=23+4+5
=212
例2.计算:
(1) x ? x5 + x2 ? x4- x3? x3;
(2)a2 ? a3 + a3? a3+ a? a4。
例2.计算:
解:(1) x ? x5 + x2 ? x4- x3? x3
(2) a2 ? a3 + a3? a3+ a? a4
=x6
=x6
= a5
= 2a5
+x6
-x6
+a6
+a5
+a6
练习
1.(口答)计算:
(1)105 ×103
(2) ? 3
=108
=
=
4
(3)(-1)6 ? (-1)4
=(-1)10
=1
(5) t 7 ?t 5
= t 12
(4) a13? a
= a14
(6) x5? x5
= x10
练习
2.下面计算对不对?如果不对,应怎样改正?
(1)a4? a4 = 2a4;
( )
( )
(2)a4? a4 = a16;
(3)a4+ a4 = a8;
(4)a4+ a4 = 2a8;
(5)a5? b3 = ab8;
(6) a5? a3 = a8。
( )
( )
( )
( )
练习
2.下面计算对不对?如果不对,应怎样改正?
(1)a4? a4 = 2a4;
( )
×
( )
×
a4? a4 = a8
(2)a4? a4 = a16;
a4? a4 = a8
(3)a4+ a4 = a8;
( )
×
a4+ a4 = 2a4
练习
2.下面计算对不对?如果不对,应怎样改正?
(5)a5? b3 = ab8;
( )
×
( )
(6) a5? a3 = a8。
a5? b3 = a5b3
( )
×
(4)a4+ a4 = 2a8;
a4+ a4 = 2a4
3.计算:
(1) a5 ? a9
(5) y ? y2 ? y3
练习
(2) y ? y7
(3) x4 ? x8
(4) x ? x2 ? x7
(6) a2 ? a6 ? a4
= a14
= y8
= x12
= x10
= y6
= a12
4.计算:
(1) x2 ? x3 + x ? x4 ;
(4) 2×23×4 + 24×22。
练习
(2) y2 ? y4 + y ? y3 ? y2 ;
(3) x3? x5 + x3? x4 - x2? x6 ;
思考
如何计算下列各式?
(-a)4?a3
a3?(-a5)
a×1+ (a+4)×1
a
1
1
a + 5
(a+5)×1+ (a-1)×1
a
1
1
a + 5
a×1+(a+5)×1-1
a
1
1
a + 5
(a-1)×1+(a+4)×1+1
a
1
1
a + 5
a(a+5)-(a-1)(a+4)
a
1
1
a + 5
同底数幂的乘法
如图,一块长为(a+5)米,宽为a米的长方形木板,长、宽各锯去1米。用代数式表示锯去木板的面积。
思考
a
1
1
a + 5
A
E
B
C
D
a
1
1
a + 5
a×1+ (a+4)×1
(a+5)×1+ (a-1)×1
a×1+(a+5)×1-1
(a-1)×1+(a+4)×1+1
a(a+5)-(a-1)(a+4)
2a+4
?
a
1
1
a + 5
课前练习
式子103,a5各表示什么意思?
103表示3个10连乘;
a5表示5个a连乘。
课前练习
指出下列各式子的底数和指数,并计算其结果。
32
(-3)2
-52
-34
3
3
2
4
=9
=9
=
=
=-25
=-81
=
=-
课前练习
化简:
(-a)4
(-a)5
=a4
= -a5
课前练习
合并下列各题中的同类项:
(1)3a3+ 2a3
(2)3a3- 3a2- a3
=5a3
=2a3 - 3a2
试一试 计算3a3? 2a3
2a3?(-3a2)
观察
下列四小题中的两个幂有什么共同之处?
(3)a3? a3;
(4)a3? a2。
(1)103×102;
(2)24×23;
10
10
2
2
a
a
a
a
同底数幂的乘法
(3)a3? a3;
(4)a3? a2。
(1)103×102;
(2)24×23;
10
10
2
2
a
a
a
a
试一试
计算下列四小题
(3)a3? a3;
(4)a3? a2。
(1)103×102;
(2)24×23;
10
10
2
2
a
a
a
a
(3)a3? a3 = a6 ;
(4)a3? a2 = a5 ,
由(1)103×102= 105 ;
(2)24×23 = 27 ;
猜想
am ? an=
(m,n都是正整数)
你能说明你的猜想的正确性吗?
am+n
从左到右的变化。
am ? an
(其中m,n都是正整数)
= a( )
= (a?a? ?a) ? (a?a? ?a)
( )个
m+n
m
n
m+n
…
…
= a? a? ? a
…
( )个
( )个
am ? an= am+n
(m,n都是正整数)
你能用自己的语言概括同底数幂相乘的运算法则吗?
am ? an= am+n
(m,n都是正整数)
同底数幂相乘的性质:
同底数幂相乘, 不变, 相加。
底数
指数
am ? an ? ap=
(m,n,p都是正整数)
am+n+p
例1.计算:
(1)107×104 ;
(2)
3 ;
?
(3) x2 ? x5 ;
(5) y ? y2 ? y3 。
(4)23×24×25 ;
例1.计算:
解:(1)107×104
(2)
3
?
=107+4
=1011
= 1+3
= 4
=
例1.计算:
(3) x2 ? x5
(5) y ? y2 ? y3
(4)23×24×25
=x2+5
=x7
=y1+2+3
=y6
=23+4+5
=212
例2.计算:
(1) x ? x5 + x2 ? x4- x3? x3;
(2)a2 ? a3 + a3? a3+ a? a4。
例2.计算:
解:(1) x ? x5 + x2 ? x4- x3? x3
(2) a2 ? a3 + a3? a3+ a? a4
=x6
=x6
= a5
= 2a5
+x6
-x6
+a6
+a5
+a6
练习
1.(口答)计算:
(1)105 ×103
(2) ? 3
=108
=
=
4
(3)(-1)6 ? (-1)4
=(-1)10
=1
(5) t 7 ?t 5
= t 12
(4) a13? a
= a14
(6) x5? x5
= x10
练习
2.下面计算对不对?如果不对,应怎样改正?
(1)a4? a4 = 2a4;
( )
( )
(2)a4? a4 = a16;
(3)a4+ a4 = a8;
(4)a4+ a4 = 2a8;
(5)a5? b3 = ab8;
(6) a5? a3 = a8。
( )
( )
( )
( )
练习
2.下面计算对不对?如果不对,应怎样改正?
(1)a4? a4 = 2a4;
( )
×
( )
×
a4? a4 = a8
(2)a4? a4 = a16;
a4? a4 = a8
(3)a4+ a4 = a8;
( )
×
a4+ a4 = 2a4
练习
2.下面计算对不对?如果不对,应怎样改正?
(5)a5? b3 = ab8;
( )
×
( )
(6) a5? a3 = a8。
a5? b3 = a5b3
( )
×
(4)a4+ a4 = 2a8;
a4+ a4 = 2a4
3.计算:
(1) a5 ? a9
(5) y ? y2 ? y3
练习
(2) y ? y7
(3) x4 ? x8
(4) x ? x2 ? x7
(6) a2 ? a6 ? a4
= a14
= y8
= x12
= x10
= y6
= a12
4.计算:
(1) x2 ? x3 + x ? x4 ;
(4) 2×23×4 + 24×22。
练习
(2) y2 ? y4 + y ? y3 ? y2 ;
(3) x3? x5 + x3? x4 - x2? x6 ;
思考
如何计算下列各式?
(-a)4?a3
a3?(-a5)
a×1+ (a+4)×1
a
1
1
a + 5
(a+5)×1+ (a-1)×1
a
1
1
a + 5
a×1+(a+5)×1-1
a
1
1
a + 5
(a-1)×1+(a+4)×1+1
a
1
1
a + 5
a(a+5)-(a-1)(a+4)
a
1
1
a + 5
