沪教版(上海)初中数学七年级第一学期 9.11 乘法公式 平方差公式 课件(21张PPT)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.11 乘法公式 平方差公式 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 18:47:52 | ||
图片预览





文档简介
一、复习引入、温故知新
温故: 多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
(a+b)(m+n)=am+an+bm+bn
an
bn
am
bm
a
b
m
n
思考1:计算下列各题,并观察下列乘式与结果的特征:
引入:
(1) (y+2)(y-2)=
(2) (3-a)(3+a)=
(3) (2a+b)(2a-b)=
用自己的语言叙述你的发现的规律
比较等号左右两边:
左边:同两个数的和与差的积
右边:这两个数的平方差
结论:两个数的和与这两个数的差的乘积等于
这两个数的平方差。
y2-22
32-a2
(2a)2-b2
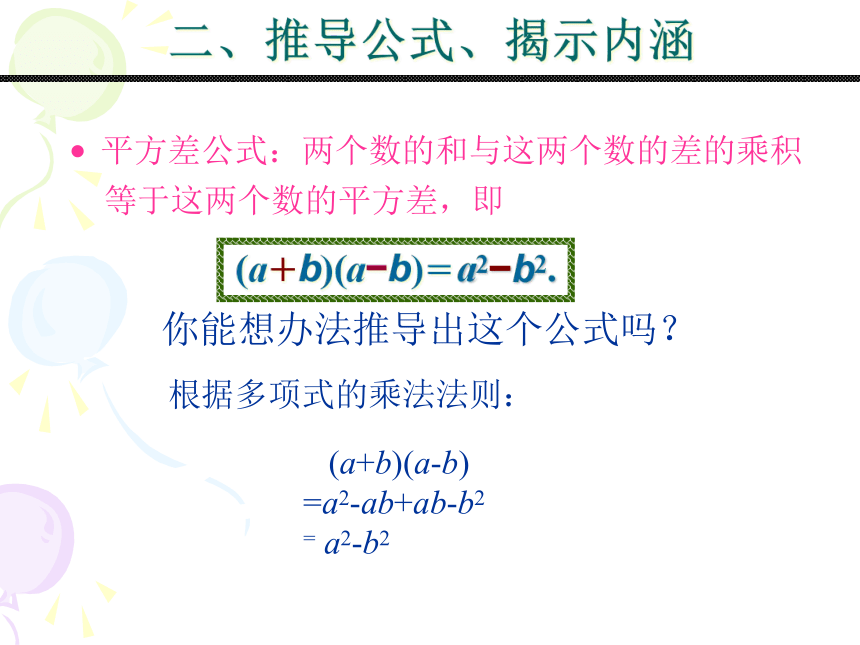
二、推导公式、揭示内涵
平方差公式:两个数的和与这两个数的差的乘积
等于这两个数的平方差,即
你能想办法推导出这个公式吗?
根据多项式的乘法法则:
(a+b)(a?b)=
a2?b2.
(a+b)(a-b)
=a2-ab+ab-b2
= a2-b2
理解平方差公式的内涵
1、公式的结构特征
符号相反的数的平方
符号相反的数
b
b
符号相同的数
a
a
完全相同的数
a
a
符号相反的数
b
b
符号相反的数
b
b
只符号相反的数
b
b
符号相反的数的平方
符号相反的数的平方
只符号相反的数的平方
完全相同的数的平方
(a+b)(a?b)=a2?b2
特征
结构
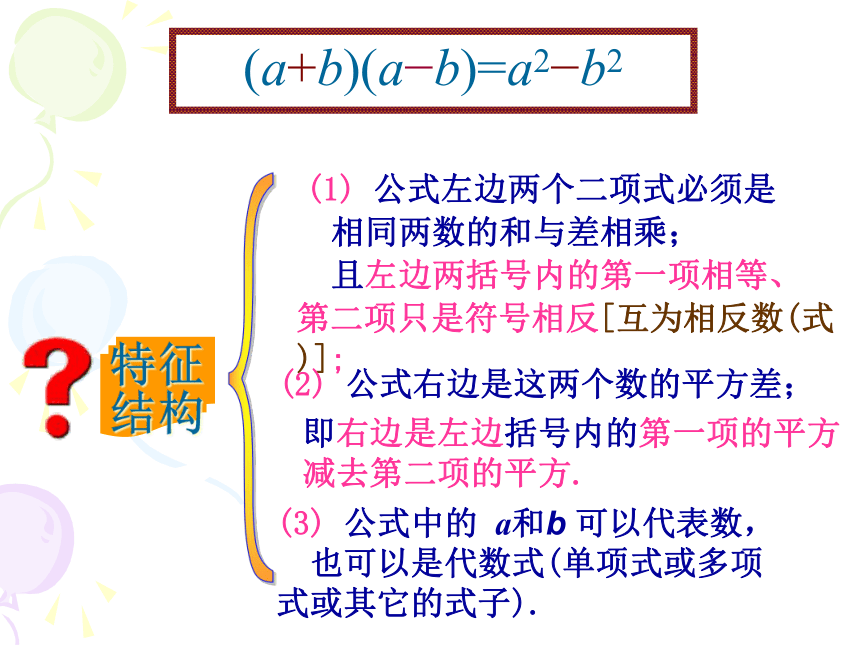
(a+b)(a?b)=a2?b2
(1) 公式左边两个二项式必须是
相同两数的和与差相乘;
且左边两括号内的第一项相等、
第二项只是符号相反[互为相反数(式)];
(2) 公式右边是这两个数的平方差;
即右边是左边括号内的第一项的平方
减去第二项的平方.
(3) 公式中的 a和b 可以代表数,
也可以是代数式(单项式或多项式或其它的式子).
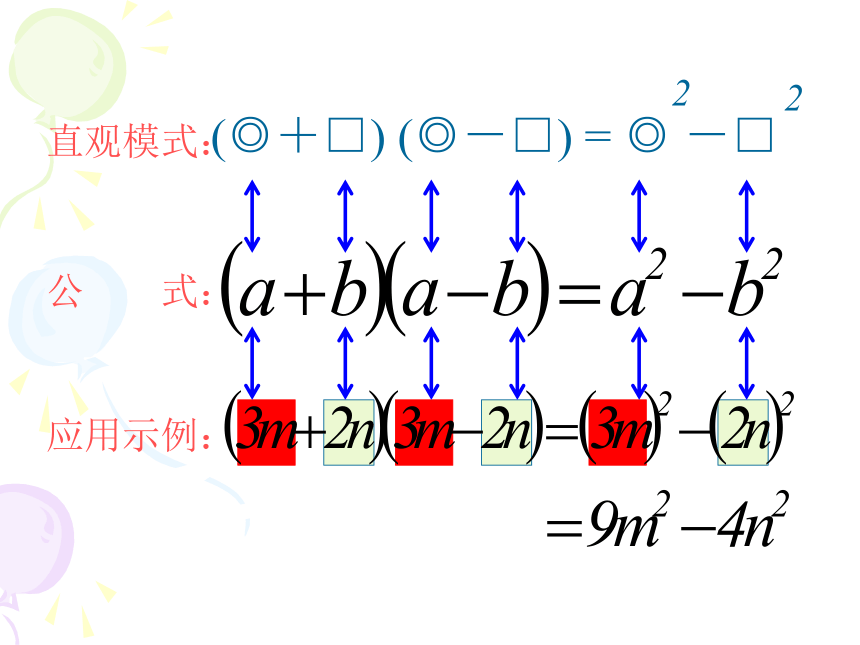
直观模式:
公 式:
应用示例:
(◎+□) (◎-□) = ◎ -□
2
2
(a+b)(a?b)=a2?b2
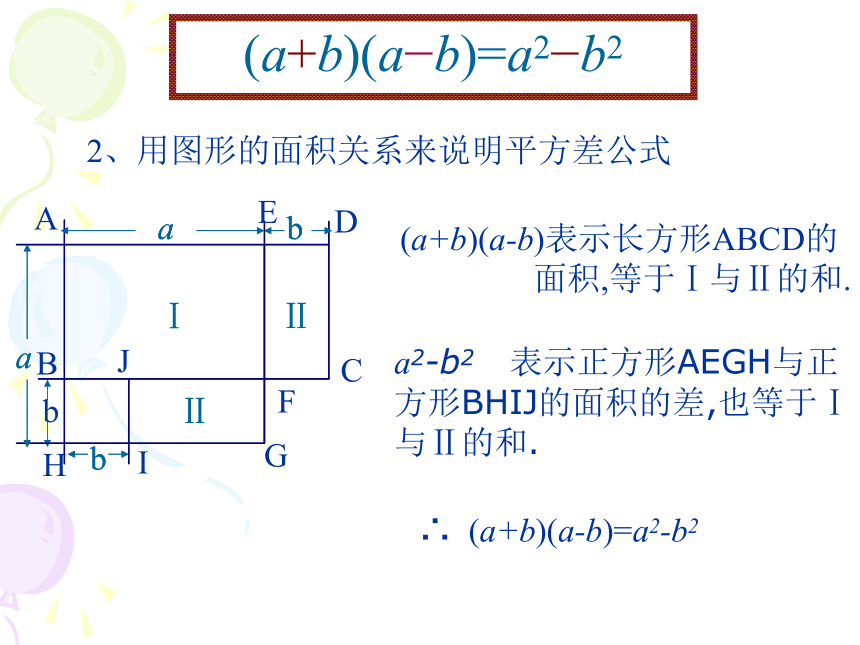
2、用图形的面积关系来说明平方差公式
(a+b)(a-b)表示长方形ABCD的
面积,等于Ⅰ与Ⅱ的和.
a2-b2 表示正方形AEGH与正
方形BHIJ的面积的差,也等于Ⅰ
与Ⅱ的和.
∴ (a+b)(a-b)=a2-b2
a
b
Ⅰ
Ⅱ
Ⅱ
b
a
A
B
C
D
E
F
G
H
a
b
Ⅰ
Ⅱ
Ⅱ
b
a
b
J
I
三、初步运用
例题1 计算:
(1) (2x+y)(2x-y);
(2)
(3) (-x+3y)(-x-3y)
(4) (a+b)(a-b)(a2+b2)
解: (1) (2x+y)(2x-y) = (2x)2-(y)2 = 4x2-y2
(a +b) (a -b)= a2 - b2
将2x看作公
式中的a,将y
看作b
(2)
( a + b ) ( a - b ) = a2 - b2
将x/2 看作a,
将y/3 看作b
三、直观运用
例题1 计算:
(1) (2x+y)(2x-y);
(2)
(3) (-x+3y)(-x-3y)
(4) (a+b)(a-b)(a2+b2)
解:
(3) (-x+3y)(-x-3y)=(-x)2-(3y)2=x2-9y2
将(-x)看作a
(3y)看作b
(4) (a+b)(a-b)(a2+b2)
= (a2-b2)(a2+b2)
= (a2)2-(b2)2
= a4-b4
将a2看作公式
中的a,将b2看作
公式中的b
(a+b)(a?b)=a2?b2
注意: 当公式中的a与b 表示的是
负数、分数、数字与字母的
积、字母与字母的积、多项
式等时, 在求它们的平方时先
应该添上括号.
意图: 学生在具体计算时比较容易出现这个错误,因此
有必要提醒学生避免计算错误.
三、神机妙算
例题2
利用平方差公式计算:
(1) 102×98 (2) 30.2×29.8
解:
102×98
= (100+2)(100-2)
= 1002-22
= 10000-4
= 9996
利用平方差公式计算
两个有理数的乘积时,
最关键的是将其写成
平方差公式的形式
30.2×29.8
= (30+0.2)(30-0.2)
= 302-0.22
= 900-0.04
= 899.96
四、尝试练习,反馈矫正
课堂练习1:
计算:
(2x+5)(2x-5);
(2) (1-2a)(1+2a);
(3) (a/3+b/2)(a/3-b/2);
(4) (x2/2+1/3)(x2/2-1/3).
意图: 学生接受知识需要一个循序渐进的过程,所以
在例题之后安排的练习比较基础,通过让学生自己练
习,加深学生对公式的结构特征的理解.
103×97
(6) 50.2×49.8
运用平方差公式时,要紧
扣公式的特征,找出相等的
“项”和符号相反的“项”,然后
应用公式.
课堂练习2:
下列两个多项式相乘,哪些可用平方差
公式?哪些不能?
(1) (2m-3n)(3n-2m); (2) (-5xy+4z)(-4y-5xz)
(4) (x+y+z)(x+y-z)
意图: 本题是公式的变式训练,可以让学生注意到
可以结合学过的运算法则将式子变形来应用公式,进
一步加深对公式的本质特征的理解.
五、拓展练习、深化提高
(3) (?4a?1)(4a?1)
解: 方法一: (位置变化)
原式= (-1-4a)(-1+4a)
= (-1)2 – (4a)2
= 1- 16a2
方法二: (符号变化)
原式= -(4a+1)(4a-1)
= -[(4a)2-12]
= -(16a2-1)
= 1- 16a2
(3) (?4a?1)(4a?1)
法一
利用加法交换律,
变成公式标准形式。
法二
提取两“?”号中的“?”号,
变成公式标准形式。
计算时千万别忘了你提出的“?”号、添括号;
注意
?
解: 原式= (x+y)2 – z2
本题是两个三项式的乘积, 将多项式
(x+y)看作公式中的a, 将z看作公式中的b.
(4) (x+y+z)(x+y-z)
符号相同
符号相反
-
( + )
( - ) =
2
2
-
( + )
( - ) =
2
2
六、归纳小结
试用语言表述平方差公式 (a+b)(a?b)=a2?b2。
两数和与这两数差的积,等于它们的平方差。
应用平方差公式 时要注意一些什么?
运用平方差公式时,要紧扣公式的特征,找出相
等的“项”和符号相反的“项”,然后应用公式;
对于不符合平方差公式标准形式者,
变成公式标准形式后,再用公式。
或提取两“?”号中的“?”号,
要利用加法交换律,
作业
1、基础训练:教材P35 练习8.11。
2、拓展训练:利用平方差公式计算:
(a+b+c)(a—b—c)。
Byebye !
温故: 多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
(a+b)(m+n)=am+an+bm+bn
an
bn
am
bm
a
b
m
n
思考1:计算下列各题,并观察下列乘式与结果的特征:
引入:
(1) (y+2)(y-2)=
(2) (3-a)(3+a)=
(3) (2a+b)(2a-b)=
用自己的语言叙述你的发现的规律
比较等号左右两边:
左边:同两个数的和与差的积
右边:这两个数的平方差
结论:两个数的和与这两个数的差的乘积等于
这两个数的平方差。
y2-22
32-a2
(2a)2-b2
二、推导公式、揭示内涵
平方差公式:两个数的和与这两个数的差的乘积
等于这两个数的平方差,即
你能想办法推导出这个公式吗?
根据多项式的乘法法则:
(a+b)(a?b)=
a2?b2.
(a+b)(a-b)
=a2-ab+ab-b2
= a2-b2
理解平方差公式的内涵
1、公式的结构特征
符号相反的数的平方
符号相反的数
b
b
符号相同的数
a
a
完全相同的数
a
a
符号相反的数
b
b
符号相反的数
b
b
只符号相反的数
b
b
符号相反的数的平方
符号相反的数的平方
只符号相反的数的平方
完全相同的数的平方
(a+b)(a?b)=a2?b2
特征
结构
(a+b)(a?b)=a2?b2
(1) 公式左边两个二项式必须是
相同两数的和与差相乘;
且左边两括号内的第一项相等、
第二项只是符号相反[互为相反数(式)];
(2) 公式右边是这两个数的平方差;
即右边是左边括号内的第一项的平方
减去第二项的平方.
(3) 公式中的 a和b 可以代表数,
也可以是代数式(单项式或多项式或其它的式子).
直观模式:
公 式:
应用示例:
(◎+□) (◎-□) = ◎ -□
2
2
(a+b)(a?b)=a2?b2
2、用图形的面积关系来说明平方差公式
(a+b)(a-b)表示长方形ABCD的
面积,等于Ⅰ与Ⅱ的和.
a2-b2 表示正方形AEGH与正
方形BHIJ的面积的差,也等于Ⅰ
与Ⅱ的和.
∴ (a+b)(a-b)=a2-b2
a
b
Ⅰ
Ⅱ
Ⅱ
b
a
A
B
C
D
E
F
G
H
a
b
Ⅰ
Ⅱ
Ⅱ
b
a
b
J
I
三、初步运用
例题1 计算:
(1) (2x+y)(2x-y);
(2)
(3) (-x+3y)(-x-3y)
(4) (a+b)(a-b)(a2+b2)
解: (1) (2x+y)(2x-y) = (2x)2-(y)2 = 4x2-y2
(a +b) (a -b)= a2 - b2
将2x看作公
式中的a,将y
看作b
(2)
( a + b ) ( a - b ) = a2 - b2
将x/2 看作a,
将y/3 看作b
三、直观运用
例题1 计算:
(1) (2x+y)(2x-y);
(2)
(3) (-x+3y)(-x-3y)
(4) (a+b)(a-b)(a2+b2)
解:
(3) (-x+3y)(-x-3y)=(-x)2-(3y)2=x2-9y2
将(-x)看作a
(3y)看作b
(4) (a+b)(a-b)(a2+b2)
= (a2-b2)(a2+b2)
= (a2)2-(b2)2
= a4-b4
将a2看作公式
中的a,将b2看作
公式中的b
(a+b)(a?b)=a2?b2
注意: 当公式中的a与b 表示的是
负数、分数、数字与字母的
积、字母与字母的积、多项
式等时, 在求它们的平方时先
应该添上括号.
意图: 学生在具体计算时比较容易出现这个错误,因此
有必要提醒学生避免计算错误.
三、神机妙算
例题2
利用平方差公式计算:
(1) 102×98 (2) 30.2×29.8
解:
102×98
= (100+2)(100-2)
= 1002-22
= 10000-4
= 9996
利用平方差公式计算
两个有理数的乘积时,
最关键的是将其写成
平方差公式的形式
30.2×29.8
= (30+0.2)(30-0.2)
= 302-0.22
= 900-0.04
= 899.96
四、尝试练习,反馈矫正
课堂练习1:
计算:
(2x+5)(2x-5);
(2) (1-2a)(1+2a);
(3) (a/3+b/2)(a/3-b/2);
(4) (x2/2+1/3)(x2/2-1/3).
意图: 学生接受知识需要一个循序渐进的过程,所以
在例题之后安排的练习比较基础,通过让学生自己练
习,加深学生对公式的结构特征的理解.
103×97
(6) 50.2×49.8
运用平方差公式时,要紧
扣公式的特征,找出相等的
“项”和符号相反的“项”,然后
应用公式.
课堂练习2:
下列两个多项式相乘,哪些可用平方差
公式?哪些不能?
(1) (2m-3n)(3n-2m); (2) (-5xy+4z)(-4y-5xz)
(4) (x+y+z)(x+y-z)
意图: 本题是公式的变式训练,可以让学生注意到
可以结合学过的运算法则将式子变形来应用公式,进
一步加深对公式的本质特征的理解.
五、拓展练习、深化提高
(3) (?4a?1)(4a?1)
解: 方法一: (位置变化)
原式= (-1-4a)(-1+4a)
= (-1)2 – (4a)2
= 1- 16a2
方法二: (符号变化)
原式= -(4a+1)(4a-1)
= -[(4a)2-12]
= -(16a2-1)
= 1- 16a2
(3) (?4a?1)(4a?1)
法一
利用加法交换律,
变成公式标准形式。
法二
提取两“?”号中的“?”号,
变成公式标准形式。
计算时千万别忘了你提出的“?”号、添括号;
注意
?
解: 原式= (x+y)2 – z2
本题是两个三项式的乘积, 将多项式
(x+y)看作公式中的a, 将z看作公式中的b.
(4) (x+y+z)(x+y-z)
符号相同
符号相反
-
( + )
( - ) =
2
2
-
( + )
( - ) =
2
2
六、归纳小结
试用语言表述平方差公式 (a+b)(a?b)=a2?b2。
两数和与这两数差的积,等于它们的平方差。
应用平方差公式 时要注意一些什么?
运用平方差公式时,要紧扣公式的特征,找出相
等的“项”和符号相反的“项”,然后应用公式;
对于不符合平方差公式标准形式者,
变成公式标准形式后,再用公式。
或提取两“?”号中的“?”号,
要利用加法交换律,
作业
1、基础训练:教材P35 练习8.11。
2、拓展训练:利用平方差公式计算:
(a+b+c)(a—b—c)。
Byebye !
