沪教版(上海)初中数学七年级第一学期 9.11 多项式与多项式相乘 课件(28张PPT)
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.11 多项式与多项式相乘 课件(28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 992.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 18:48:40 | ||
图片预览


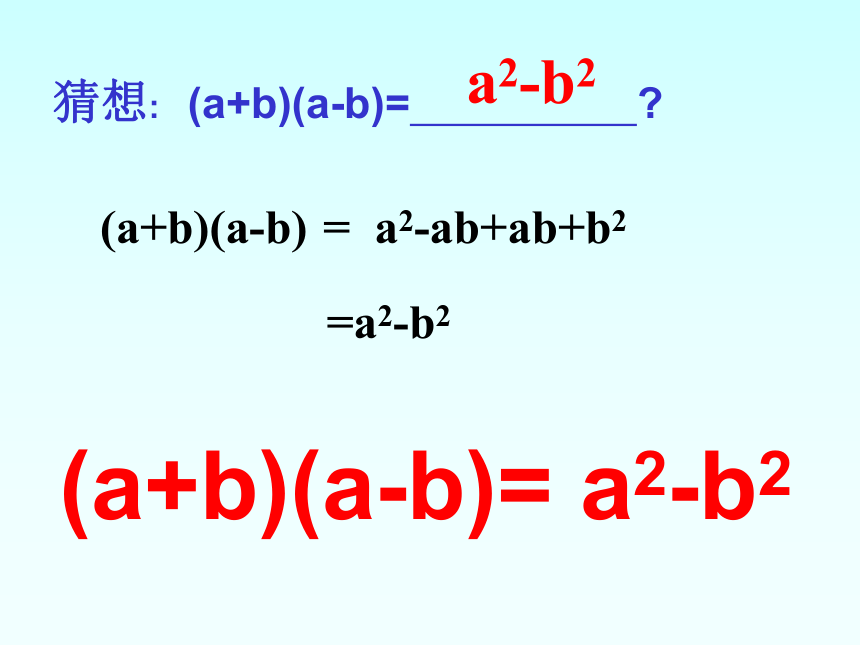


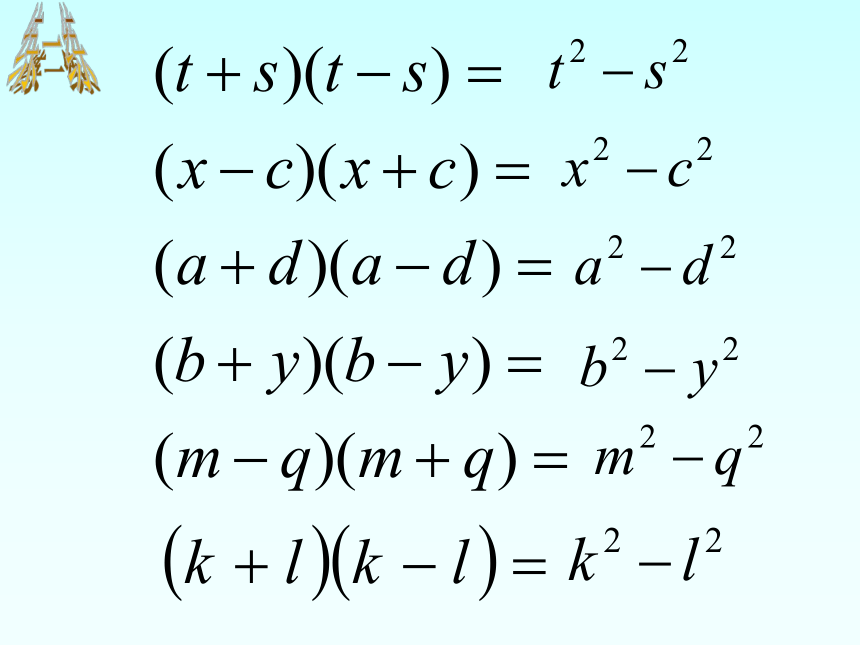


文档简介
多项式与多项式相乘
①
②
③
④
①
②
③
④
复习引入:
计算下列多项式的积:
(1) (x-1)(y-2)= ;
(2) (x+1)(x+5) ;
(3) (x+y)(x-y) ;
(4) (m+n)(m-n) ;
(5) (2x+1)(2x-1) ;
[想一想] (3),(4),(5)这几道题目有什么共同特点?
从计算结果你能发现什么规律?
= x2-y2
= m2-n2
= 4x2-1
= (2x)2-12
xy-2x-y+2
(x2+5x+x+5)
= x2+6x+5
(x2-xy+xy-9)
(m2-mn+mn-n2 )
(4x2-2x+2x-1)
猜想: (a+b)(a-b)= ?
a2-b2
(a+b)(a-b) =
a2-ab+ab+b2
=a2-b2
(a+b)(a-b)= a2-b2
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差.
公式的结构特征:
(1)左边是两个二项式相乘,这两项中有一
项完全相同,另一项互为相反数.
(2)右边是乘式中两项的平方差
(相同项)2 - (相反项)2
9.11
(a 相同项)
(b 相反项)
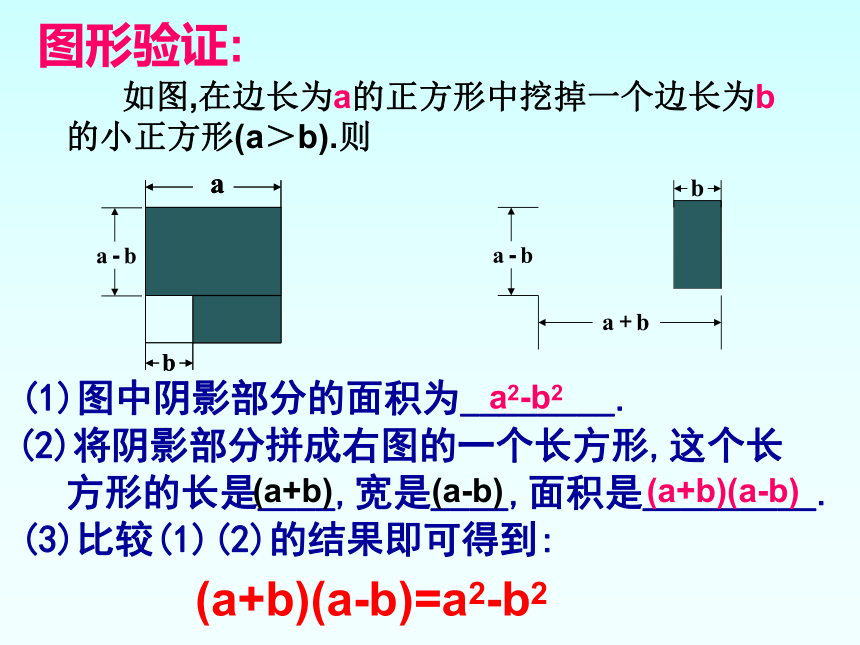
(1)图中阴影部分的面积为________.
(2)将阴影部分拼成右图的一个长方形,这个长
方形的长是____,宽是____,面积是_________.
(3)比较(1)(2)的结果即可得到:
(a+b)(a-b)=a2-b2
如图,在边长为a的正方形中挖掉一个边长为b
的小正方形(a>b).则
a2-b2
(a+b)(a-b)
(a+b)
(a-b)
图形验证:
练习一: (口答)
(1) (x+y)(x-y)=
(2) (c+d)(c-d)=
(3) (p+q)(p-q)=
(4) (r+s)(r-s)=
(5) (u+v)(u-v)=
(6) (k+t)(k-t)=
x2-y2
c2-d2
p2-q2
r2-s2
u2-v2
k2-t2
练习二: (口答)
(1) (x+1)(x-1)=
(2) (x-4)(x+4)=
(3) (3+y)(3-y)=
(4) (y-5)(y+5)=
(5) (m+7)(m-7)=
(6) (8-m)(8+m)=
(7) (t+9)(t-9)=
x2-1
x2-16
9-y2
y2-25
m2-49
64-m2
t2-81
【例1】运用平方差公式计算:
( a + b )( a - b ) = a 2 - b 2
解:
=
( )2
-
( )2
2x2
(3x+2)(3x-2)
(2y+5)(2y-5)
(3)
(4)
(5) (1-2a)(1+2a)
(6) (b+2a)(2a-b)
练习三: 用平方差公式计算
9x2-4
4y2-25
1-4a2
4a2-b2
试一试:
(能口答吗?)
(1) ( -3X+2)(-3X-2)
(2) ( -3X-2)(3X-2)
(3) (2-3X)(3X+2)
= (-3x)2-22
= (-2)2-(3x)2
= 22-(3x)2
例2: 计算
= 9x2-4
= 4-9x2
= 4-9x2
解:原式
解:原式
解:原式
a 2
b 3x
a -2
b 3x
a -3x
b 2
平方差公式的实质:
(a+b)(a-b)=a2-b2
两个多项式相乘,只要既有相同项,又有相反项,并且不含有其他的项,就可以使用此公式.
(1) 与项的书写位置无关;
与相同项的符号无关,相同项可以是同“+”,
也可以是同“-”。
一条件:
两无关:
(4) (-2a-3b)(3b-2a)
(5) (2a+3b)(-2a+3b)
(6) (2a-3b)(-3b-2a)
= 4a2-9b2
= 9b2-4a2
= 9b2-4a2
a -2a b 3b
a 3b b 2a
a -3b b 2a
试一试; (能一步出答案吗?)
判断下列式子是否可用平方差公式。
(1) (-a+b)(a+b) (2) (-a+b)(a-b)
(3) (a+b)(a-c) (4) (2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7) (-4k3+3y2)(-4k3-3y2)
是
否
是
是
是
是
否
b2-a2
a2-4
x2-1
16k6-9y4
没有相同项
没有相反项
请你判断下列计算对不对?为什么?
(x2+2)(x2-2)=x4-2 ( )
(4x-6)(4x+6)=4x2-36 ( )
(2x+3)(x-3)=2x2-9 ( )
(5ab+1)(5ab-1)=25a2b2-1 ( )
(mn-1)(mn+1)=mn2-1 ( )
×
√
×
×
×
x4- 4
16x2-36
不可用公式
m2n2-1
【例3】用平方差公式计算:
(1) 102×98
解:(1) 原式=(100+2)(100-2)
=1002-22
=10000-4
=9996
(2) 30.2×29.8
(3) 79×81
(4)
(2) (30+0.2)(30-0.2)
(3) (80-1)(80+1)
(4)
例4: 利用平方差计算:
(1) (2a+b)(2a-b)(4a2+b)
(2) (3x+4)(3x-4)-(2x+3)(3x-2)
(3) (a+2b+2c)(a+2b-2c)
解:原式=[( )+( )][( )-( )]
=(a+2b)2-(2c)2
=a2+4ab+4b2-4c2
2a+b
2a+b
2c
2c
(a+b)(a-b)=a2-b2
a,b也可以表示
多项式
练习四: 将下列各式变形为可利用平方差
公式计算的形式:
1) (a+2b+3)(a+2b-3)
2) (a+2b-3)(a-2b+3)
3) (a-2b+3)(a-2b-3)
4) (a-2b-3)(a+2b-3)
5) (3a-5b-2c)(-3a-5b+2c)
6) (x+y+m+n)(x+y-m-n)
[(a+2b)+3][(a+2b)-3]
[a+(2b-3)] [a-(2b-3)]
[(a-2b)+3] [(a-2b)-3]
[(a-3)-2b] [(a-3)+2b]
[(-5b)+(3a-2c)] [(-5b)-(3a-2c)]
[(x+y)+(m+n)][(x+y)-(m+n)]
练习五 计算:
(y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
–4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2 + )(x- )
1. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。
两数和与这两数差的积,等于这两数的平方差。
2. 应用平方差公式的条件是什么?
运用平方差公式时,要紧扣公式的实质,找出相同
的“项”和符号相反的“项”,然后应用公式;
3.公式中的a,b可以代表数, 字母,单项式或者多项式.
小结
两个多项式相乘,只要既有相同项,又有相反项,并且不含有其他的项,就可以使用此公式.
添括号时,如果括号前面是正号,括到括号里的 各项都不变号;如果括号前面是负号,括到括号里 各项都改变符号。
4.
说明:平方差公式也可以逆用,
即:a2-b2=(a+b)(a-b)
1.下列多项式相乘,正确的有( )
(1)(a+b-c)(a-b+c)=a2-(b-c)2
(2)(a-b+c)(-a+b-c)=b2-(a+c)2
(3)(a-b+c)a-b-c)=a2-(b-c)2
(4)(a+b-c)(a-b+c)=(b-c)2-a2
A.1 个 B.2 个 C.3 个 D.4个
A
2、巧算:99×101× 10001
4、计算:
1002-992+982-972+….+22-12
3、已知:(m+35)2=13302921,
求(m+45)(m+25)的值。
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:1) (y+2)(y-2) - (3-y)(3+y)
= (y2-4) –(9-y2)
= y2-4 –9+y2
= 2y2-13
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
= -16y2+1+12y2-12y-9
= -4y2-12y-8
解:3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
= -4(4y2- )+3(4y2+2y-6y-3)
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:4) (x+ )(x2+ )(x- )
= [(x+ )(x- )](x2+ )
= (x2- )(x2+ )
= x4-
再见
①
②
③
④
①
②
③
④
复习引入:
计算下列多项式的积:
(1) (x-1)(y-2)= ;
(2) (x+1)(x+5) ;
(3) (x+y)(x-y) ;
(4) (m+n)(m-n) ;
(5) (2x+1)(2x-1) ;
[想一想] (3),(4),(5)这几道题目有什么共同特点?
从计算结果你能发现什么规律?
= x2-y2
= m2-n2
= 4x2-1
= (2x)2-12
xy-2x-y+2
(x2+5x+x+5)
= x2+6x+5
(x2-xy+xy-9)
(m2-mn+mn-n2 )
(4x2-2x+2x-1)
猜想: (a+b)(a-b)= ?
a2-b2
(a+b)(a-b) =
a2-ab+ab+b2
=a2-b2
(a+b)(a-b)= a2-b2
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差.
公式的结构特征:
(1)左边是两个二项式相乘,这两项中有一
项完全相同,另一项互为相反数.
(2)右边是乘式中两项的平方差
(相同项)2 - (相反项)2
9.11
(a 相同项)
(b 相反项)
(1)图中阴影部分的面积为________.
(2)将阴影部分拼成右图的一个长方形,这个长
方形的长是____,宽是____,面积是_________.
(3)比较(1)(2)的结果即可得到:
(a+b)(a-b)=a2-b2
如图,在边长为a的正方形中挖掉一个边长为b
的小正方形(a>b).则
a2-b2
(a+b)(a-b)
(a+b)
(a-b)
图形验证:
练习一: (口答)
(1) (x+y)(x-y)=
(2) (c+d)(c-d)=
(3) (p+q)(p-q)=
(4) (r+s)(r-s)=
(5) (u+v)(u-v)=
(6) (k+t)(k-t)=
x2-y2
c2-d2
p2-q2
r2-s2
u2-v2
k2-t2
练习二: (口答)
(1) (x+1)(x-1)=
(2) (x-4)(x+4)=
(3) (3+y)(3-y)=
(4) (y-5)(y+5)=
(5) (m+7)(m-7)=
(6) (8-m)(8+m)=
(7) (t+9)(t-9)=
x2-1
x2-16
9-y2
y2-25
m2-49
64-m2
t2-81
【例1】运用平方差公式计算:
( a + b )( a - b ) = a 2 - b 2
解:
=
( )2
-
( )2
2x2
(3x+2)(3x-2)
(2y+5)(2y-5)
(3)
(4)
(5) (1-2a)(1+2a)
(6) (b+2a)(2a-b)
练习三: 用平方差公式计算
9x2-4
4y2-25
1-4a2
4a2-b2
试一试:
(能口答吗?)
(1) ( -3X+2)(-3X-2)
(2) ( -3X-2)(3X-2)
(3) (2-3X)(3X+2)
= (-3x)2-22
= (-2)2-(3x)2
= 22-(3x)2
例2: 计算
= 9x2-4
= 4-9x2
= 4-9x2
解:原式
解:原式
解:原式
a 2
b 3x
a -2
b 3x
a -3x
b 2
平方差公式的实质:
(a+b)(a-b)=a2-b2
两个多项式相乘,只要既有相同项,又有相反项,并且不含有其他的项,就可以使用此公式.
(1) 与项的书写位置无关;
与相同项的符号无关,相同项可以是同“+”,
也可以是同“-”。
一条件:
两无关:
(4) (-2a-3b)(3b-2a)
(5) (2a+3b)(-2a+3b)
(6) (2a-3b)(-3b-2a)
= 4a2-9b2
= 9b2-4a2
= 9b2-4a2
a -2a b 3b
a 3b b 2a
a -3b b 2a
试一试; (能一步出答案吗?)
判断下列式子是否可用平方差公式。
(1) (-a+b)(a+b) (2) (-a+b)(a-b)
(3) (a+b)(a-c) (4) (2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7) (-4k3+3y2)(-4k3-3y2)
是
否
是
是
是
是
否
b2-a2
a2-4
x2-1
16k6-9y4
没有相同项
没有相反项
请你判断下列计算对不对?为什么?
(x2+2)(x2-2)=x4-2 ( )
(4x-6)(4x+6)=4x2-36 ( )
(2x+3)(x-3)=2x2-9 ( )
(5ab+1)(5ab-1)=25a2b2-1 ( )
(mn-1)(mn+1)=mn2-1 ( )
×
√
×
×
×
x4- 4
16x2-36
不可用公式
m2n2-1
【例3】用平方差公式计算:
(1) 102×98
解:(1) 原式=(100+2)(100-2)
=1002-22
=10000-4
=9996
(2) 30.2×29.8
(3) 79×81
(4)
(2) (30+0.2)(30-0.2)
(3) (80-1)(80+1)
(4)
例4: 利用平方差计算:
(1) (2a+b)(2a-b)(4a2+b)
(2) (3x+4)(3x-4)-(2x+3)(3x-2)
(3) (a+2b+2c)(a+2b-2c)
解:原式=[( )+( )][( )-( )]
=(a+2b)2-(2c)2
=a2+4ab+4b2-4c2
2a+b
2a+b
2c
2c
(a+b)(a-b)=a2-b2
a,b也可以表示
多项式
练习四: 将下列各式变形为可利用平方差
公式计算的形式:
1) (a+2b+3)(a+2b-3)
2) (a+2b-3)(a-2b+3)
3) (a-2b+3)(a-2b-3)
4) (a-2b-3)(a+2b-3)
5) (3a-5b-2c)(-3a-5b+2c)
6) (x+y+m+n)(x+y-m-n)
[(a+2b)+3][(a+2b)-3]
[a+(2b-3)] [a-(2b-3)]
[(a-2b)+3] [(a-2b)-3]
[(a-3)-2b] [(a-3)+2b]
[(-5b)+(3a-2c)] [(-5b)-(3a-2c)]
[(x+y)+(m+n)][(x+y)-(m+n)]
练习五 计算:
(y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
–4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2 + )(x- )
1. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。
两数和与这两数差的积,等于这两数的平方差。
2. 应用平方差公式的条件是什么?
运用平方差公式时,要紧扣公式的实质,找出相同
的“项”和符号相反的“项”,然后应用公式;
3.公式中的a,b可以代表数, 字母,单项式或者多项式.
小结
两个多项式相乘,只要既有相同项,又有相反项,并且不含有其他的项,就可以使用此公式.
添括号时,如果括号前面是正号,括到括号里的 各项都不变号;如果括号前面是负号,括到括号里 各项都改变符号。
4.
说明:平方差公式也可以逆用,
即:a2-b2=(a+b)(a-b)
1.下列多项式相乘,正确的有( )
(1)(a+b-c)(a-b+c)=a2-(b-c)2
(2)(a-b+c)(-a+b-c)=b2-(a+c)2
(3)(a-b+c)a-b-c)=a2-(b-c)2
(4)(a+b-c)(a-b+c)=(b-c)2-a2
A.1 个 B.2 个 C.3 个 D.4个
A
2、巧算:99×101× 10001
4、计算:
1002-992+982-972+….+22-12
3、已知:(m+35)2=13302921,
求(m+45)(m+25)的值。
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:1) (y+2)(y-2) - (3-y)(3+y)
= (y2-4) –(9-y2)
= y2-4 –9+y2
= 2y2-13
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
= -16y2+1+12y2-12y-9
= -4y2-12y-8
解:3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
= -4(4y2- )+3(4y2+2y-6y-3)
5.计算:
1) (y+2)(y-2) - (3-y)(3+y)
2) –3x(x+1)(x-1) - x(3x+2)(2-3x)
3) –4(2y- )( +2y) + 3(2y-3)(2y+1)
4) (x+ )(x2+ )(x- )
解:4) (x+ )(x2+ )(x- )
= [(x+ )(x- )](x2+ )
= (x2- )(x2+ )
= x4-
再见
