22.6 三角形的中位线 课件(共24张PPT)
文档属性
| 名称 | 22.6 三角形的中位线 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 813.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 17:51:19 | ||
图片预览




文档简介
22.6三角形的中位线
在一块由考古学家发现的古巴比伦泥版上记载着这样一个有趣的故事:在巴比伦两河流域,有四位兄弟本来相安无事的生活着,直到有一天他们父亲的去世打破了这一平静,大家为了分割父亲留下的一块土地而争论不休,谁都不肯吃亏,土地为三角形形状,请同学们利用所学的数学知识设计方法帮助这四位兄弟解决矛盾,回归平静生活,同时也要对自己设计的方法有所说明,来说服四兄弟停止争论。
课前预习
小组讨论结果:
课前预习
第三组
第四组
第二组
第一组
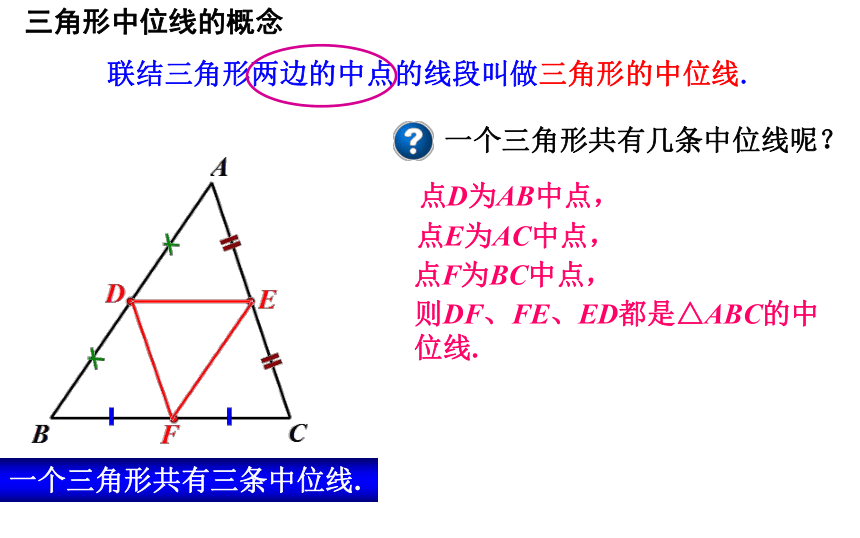
三角形中位线的概念
联结三角形两边的中点的线段叫做三角形的中位线.
一个三角形共有几条中位线呢?
点D为AB中点,
点E为AC中点,
点F为BC中点,
则DF、FE、ED都是△ABC的中位线.
一个三角形共有三条中位线.
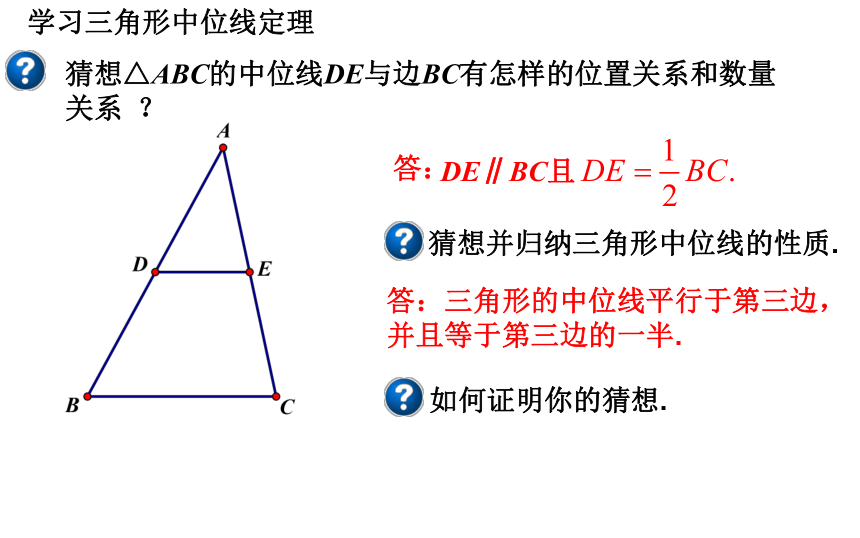
学习三角形中位线定理
猜想△ABC的中位线DE与边BC有怎样的位置关系和数量关系 ?
DE∥BC且
答:
猜想并归纳三角形中位线的性质.
如何证明你的猜想.
答:三角形的中位线平行于第三边,
并且等于第三边的一半.
∴四边形BCFD是平行四边形
(一组对边平行且相等的四边形是平行四边形),
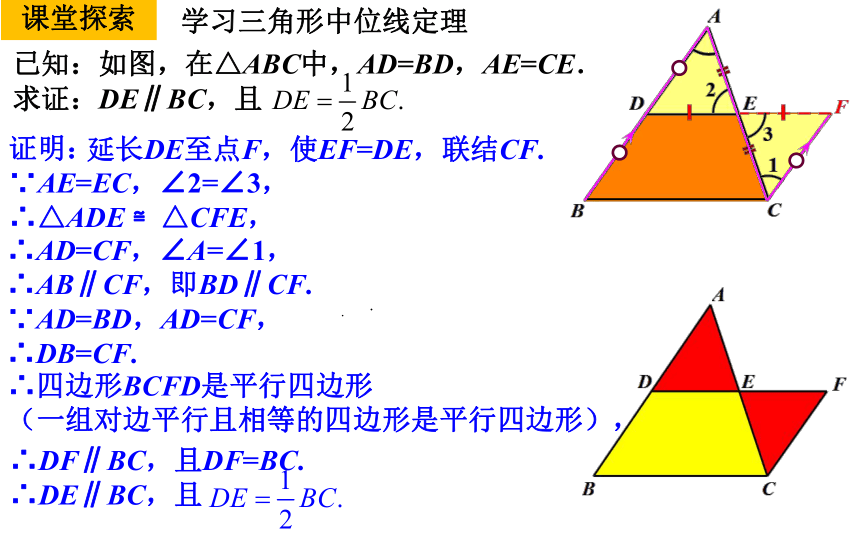
已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且
.
延长DE至点F,使EF=DE,联结CF.
证明:
∵AE=EC,∠2=∠3,
∴△ADE ≌△CFE,
∴AD=CF,∠A=∠1,
∴AB∥CF,即BD∥CF.
∵AD=BD,AD=CF,
∴DB=CF.
∴DF∥BC,且DF=BC.
∴DE∥BC,且
.
学习三角形中位线定理
课堂探索
三角形中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
在△ABC中,
∵ AD=BD,AE=CE,
∴ DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
符号语言:
新知运用
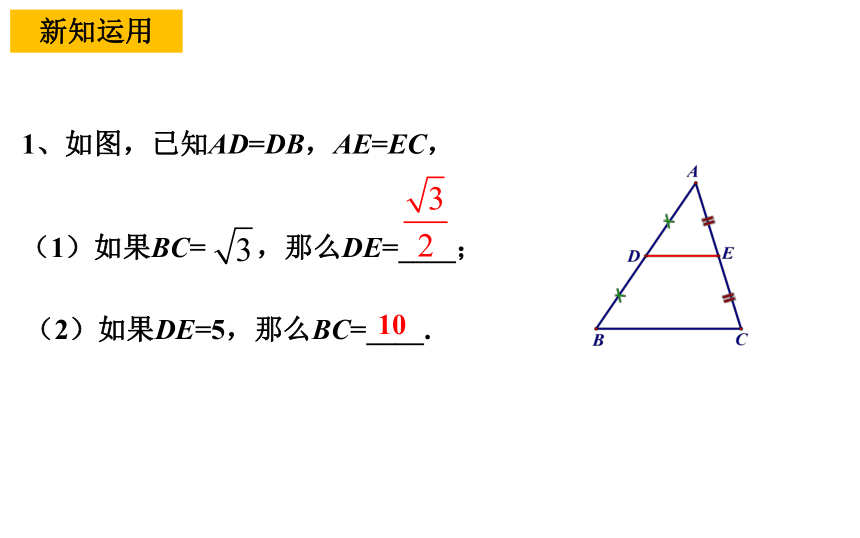
(2)如果DE=5,那么BC=____.
10
1、如图,已知AD=DB,AE=EC,
(1)如果BC= ,那么DE=____;
例题讲解
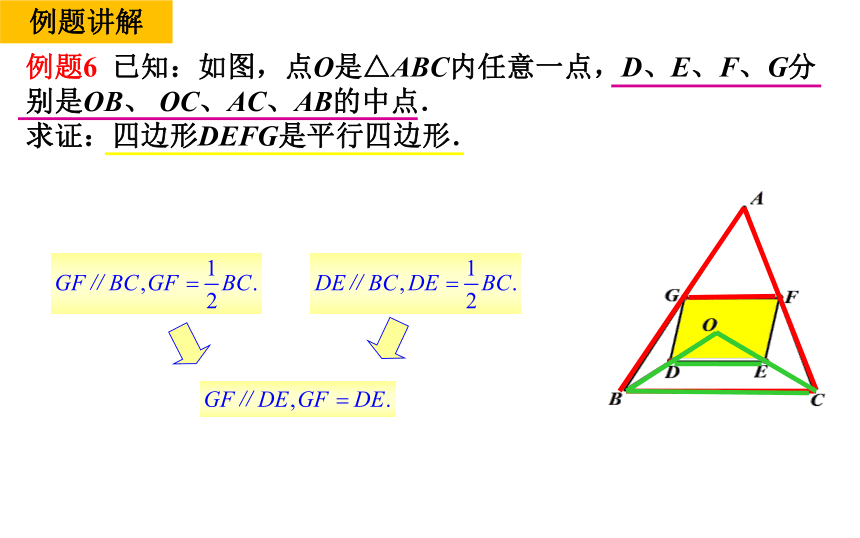
例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
例题讲解
例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
证明:∵ 点G、F分别为AB、AC的中点,
∴ GF∥BC,且
(三角形的中位线平行于第三边,
并且等于第三边的一半).
同理:DE∥BC,且 .
∴GF∥DE,且GF=DE.
∴四边形DEFG是平行四边形
(一组对边平行且相等的四边形是平行四边形).
变式一 已知:如图,点O是△ABC外内任意一点,D、E、F、G分别是OB、OC、AC、AB的中点.四边形DEFG还是平行四边形吗?说明理由.
求证:顺次联结四边形四条边的中点,所得的四边形是平行四边形.
已知:如图,四边形AOBC中,D、E、F、G分别是OB、OC、AC、AB的中点,
求证:四边形DEFG是平行四边形.
证明:联结BC.
变式二:
1、平行四边形的“中点四边形”是 .
2、矩形的“中点四边形”是 .
3、菱形的“中点四边形”是 .
4、正方形的“中点四边形”是 .
5、对角线互相垂直的四边形的“中点四边形”是 .
6、对角线相等的四边形的“中点四边形”是 .
7、对角线相等且互相垂直的四边形的“中点四边形”是
.
小组讨论
填空:
1、平行四边形的“中点四边形”是 .
平行四边形
2、矩形的“中点四边形”是 .
菱形
3、菱形的“中点四边形”是 .
矩形
4、正方形的“中点四边形”是 .
正方形
5、对角线互相垂直的四边形的“中点四边形”是 .
矩形
切换几何画板
6、对角线相等的四边形的“中点四边形”是 .
7、对角线相等且互相垂直的四边形的“中点四边形”是
.
菱形
正方形
小组讨论
填空:
通过本课的学习你有何收获?
课堂小结
1、三角形中位线的概念
在△ABC中,
∵ AD=BD,AE=CE,
∴ DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
2、三角形中位线定理
联结三角形两边的中点的线段叫做三角形的中位线.
布置作业
练习册 习题22.6(1)
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
移动平行线,是否存在某个特殊
的位置,恰好使分割得的梯形和
三角形拼成一个平行四边形?
答:存在的,点E是AC的中点.
怎么拼?
答:若平行线与AB边交于点D,
将△AED绕点E旋转180°,
即得到□DBCD′.
切换几何画板
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
为什么拼出的图形是平行四边形?
图形的旋转
△ADE≌△CD′E
∠A=∠1
AB∥CD′
DE∥BC
四边形DBCD′是平行四边形
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
这时,点D位于线段AB的什么位置上?
答:由于CD′=DB ,且CD′=AD,所以AD=BD,点D是AB的中点.
点D、E分别是△ABC的边AB、AC的中点,
则线段DE是△ABC的一条特殊线段.
为什么拼出的图形是平行四边形?
适时小结
三角形的中位线与三角形的中线的区别.
三角形
概念
图形
中位线
中线
联结两边中点的线段.
联结顶点与
其对边中点的线段.
两边中点
一顶点
一中点
平行四边形的“中点四边形”是 .
平行四边形
矩形的“中点四边形”是 .
菱形
菱形的“中点四边形”是 .
矩形
正方形的“中点四边形”是 .
正方形
对角线互相垂直的四边形的“中点四边形”是 .
矩形
切换几何画板
对角线相等的四边形的“中点四边形”是 .
对角线相等且互相垂直的四边形的“中点四边形”是
.
菱形
正方形
小组讨论
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DE和中线AE互相平分.
证明:联结ED、EF.
∵D、E分别是AB、BC的中点,
∴DE∥AC(三角形的中位线平行于第三边).
同理:EF∥AB,
∴四边形DEFA是平行四边形(平行四边形的定义).
∴中位线DE和中线AE互相平分
(平行四边形的对角线互相平分).
适时小结:
已知两边中点构造三角形的中位线是
常用的添辅助线的方法之一.
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DE和中线AE互相平分.
分析:
在一块由考古学家发现的古巴比伦泥版上记载着这样一个有趣的故事:在巴比伦两河流域,有四位兄弟本来相安无事的生活着,直到有一天他们父亲的去世打破了这一平静,大家为了分割父亲留下的一块土地而争论不休,谁都不肯吃亏,土地为三角形形状,请同学们利用所学的数学知识设计方法帮助这四位兄弟解决矛盾,回归平静生活,同时也要对自己设计的方法有所说明,来说服四兄弟停止争论。
课前预习
小组讨论结果:
课前预习
第三组
第四组
第二组
第一组
三角形中位线的概念
联结三角形两边的中点的线段叫做三角形的中位线.
一个三角形共有几条中位线呢?
点D为AB中点,
点E为AC中点,
点F为BC中点,
则DF、FE、ED都是△ABC的中位线.
一个三角形共有三条中位线.
学习三角形中位线定理
猜想△ABC的中位线DE与边BC有怎样的位置关系和数量关系 ?
DE∥BC且
答:
猜想并归纳三角形中位线的性质.
如何证明你的猜想.
答:三角形的中位线平行于第三边,
并且等于第三边的一半.
∴四边形BCFD是平行四边形
(一组对边平行且相等的四边形是平行四边形),
已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且
.
延长DE至点F,使EF=DE,联结CF.
证明:
∵AE=EC,∠2=∠3,
∴△ADE ≌△CFE,
∴AD=CF,∠A=∠1,
∴AB∥CF,即BD∥CF.
∵AD=BD,AD=CF,
∴DB=CF.
∴DF∥BC,且DF=BC.
∴DE∥BC,且
.
学习三角形中位线定理
课堂探索
三角形中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
在△ABC中,
∵ AD=BD,AE=CE,
∴ DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
符号语言:
新知运用
(2)如果DE=5,那么BC=____.
10
1、如图,已知AD=DB,AE=EC,
(1)如果BC= ,那么DE=____;
例题讲解
例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
例题讲解
例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
证明:∵ 点G、F分别为AB、AC的中点,
∴ GF∥BC,且
(三角形的中位线平行于第三边,
并且等于第三边的一半).
同理:DE∥BC,且 .
∴GF∥DE,且GF=DE.
∴四边形DEFG是平行四边形
(一组对边平行且相等的四边形是平行四边形).
变式一 已知:如图,点O是△ABC外内任意一点,D、E、F、G分别是OB、OC、AC、AB的中点.四边形DEFG还是平行四边形吗?说明理由.
求证:顺次联结四边形四条边的中点,所得的四边形是平行四边形.
已知:如图,四边形AOBC中,D、E、F、G分别是OB、OC、AC、AB的中点,
求证:四边形DEFG是平行四边形.
证明:联结BC.
变式二:
1、平行四边形的“中点四边形”是 .
2、矩形的“中点四边形”是 .
3、菱形的“中点四边形”是 .
4、正方形的“中点四边形”是 .
5、对角线互相垂直的四边形的“中点四边形”是 .
6、对角线相等的四边形的“中点四边形”是 .
7、对角线相等且互相垂直的四边形的“中点四边形”是
.
小组讨论
填空:
1、平行四边形的“中点四边形”是 .
平行四边形
2、矩形的“中点四边形”是 .
菱形
3、菱形的“中点四边形”是 .
矩形
4、正方形的“中点四边形”是 .
正方形
5、对角线互相垂直的四边形的“中点四边形”是 .
矩形
切换几何画板
6、对角线相等的四边形的“中点四边形”是 .
7、对角线相等且互相垂直的四边形的“中点四边形”是
.
菱形
正方形
小组讨论
填空:
通过本课的学习你有何收获?
课堂小结
1、三角形中位线的概念
在△ABC中,
∵ AD=BD,AE=CE,
∴ DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
2、三角形中位线定理
联结三角形两边的中点的线段叫做三角形的中位线.
布置作业
练习册 习题22.6(1)
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
移动平行线,是否存在某个特殊
的位置,恰好使分割得的梯形和
三角形拼成一个平行四边形?
答:存在的,点E是AC的中点.
怎么拼?
答:若平行线与AB边交于点D,
将△AED绕点E旋转180°,
即得到□DBCD′.
切换几何画板
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
为什么拼出的图形是平行四边形?
图形的旋转
△ADE≌△CD′E
∠A=∠1
AB∥CD′
DE∥BC
四边形DBCD′是平行四边形
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
这时,点D位于线段AB的什么位置上?
答:由于CD′=DB ,且CD′=AD,所以AD=BD,点D是AB的中点.
点D、E分别是△ABC的边AB、AC的中点,
则线段DE是△ABC的一条特殊线段.
为什么拼出的图形是平行四边形?
适时小结
三角形的中位线与三角形的中线的区别.
三角形
概念
图形
中位线
中线
联结两边中点的线段.
联结顶点与
其对边中点的线段.
两边中点
一顶点
一中点
平行四边形的“中点四边形”是 .
平行四边形
矩形的“中点四边形”是 .
菱形
菱形的“中点四边形”是 .
矩形
正方形的“中点四边形”是 .
正方形
对角线互相垂直的四边形的“中点四边形”是 .
矩形
切换几何画板
对角线相等的四边形的“中点四边形”是 .
对角线相等且互相垂直的四边形的“中点四边形”是
.
菱形
正方形
小组讨论
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DE和中线AE互相平分.
证明:联结ED、EF.
∵D、E分别是AB、BC的中点,
∴DE∥AC(三角形的中位线平行于第三边).
同理:EF∥AB,
∴四边形DEFA是平行四边形(平行四边形的定义).
∴中位线DE和中线AE互相平分
(平行四边形的对角线互相平分).
适时小结:
已知两边中点构造三角形的中位线是
常用的添辅助线的方法之一.
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DE和中线AE互相平分.
分析:
