华东师大版八年级数学上册 14.1.1 直角三角形三边的关系 勾股定理 课件(共24张PPT)
文档属性
| 名称 | 华东师大版八年级数学上册 14.1.1 直角三角形三边的关系 勾股定理 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:24:46 | ||
图片预览

文档简介
14.1.1勾股定理
直角三角形三边的关系
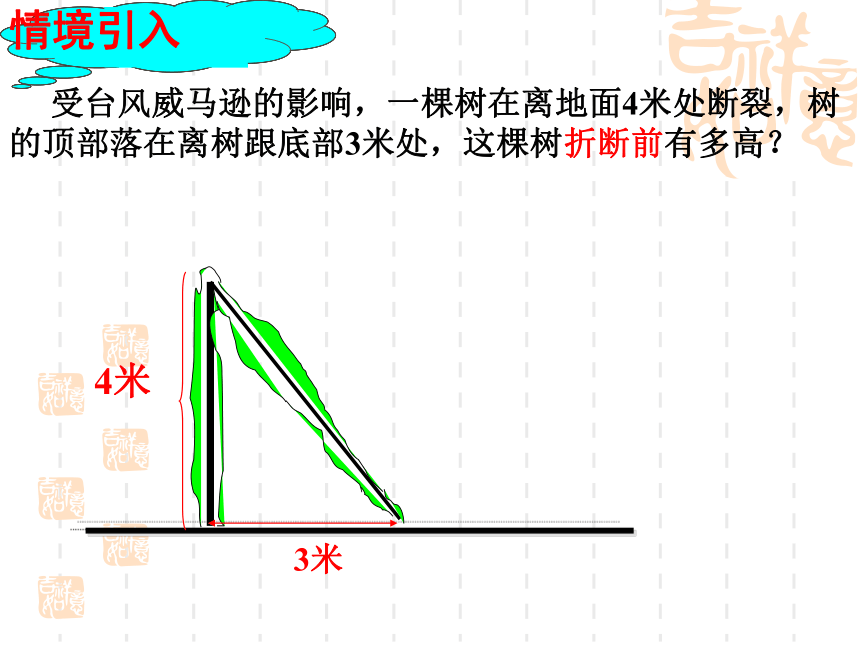
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
y=0
情境引入
R
Q
P
C
A
B
图14.1.1
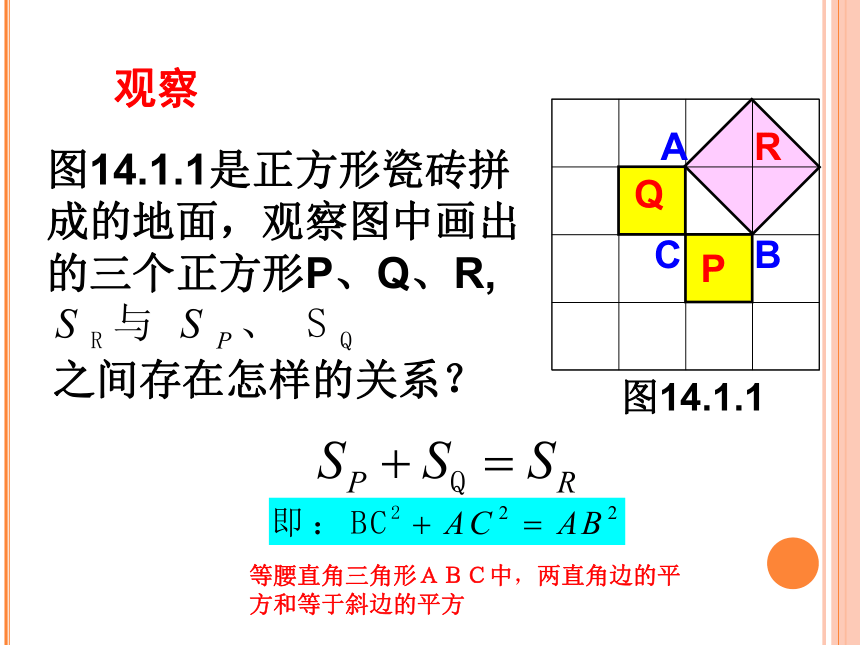
图14.1.1是正方形瓷砖拼成的地面,观察图中画出的三个正方形P、Q、R,
之间存在怎样的关系?
观察
等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
A
B
C
P
Q
R
试一试
(每一小方格表示1cm2)
图14.1.2
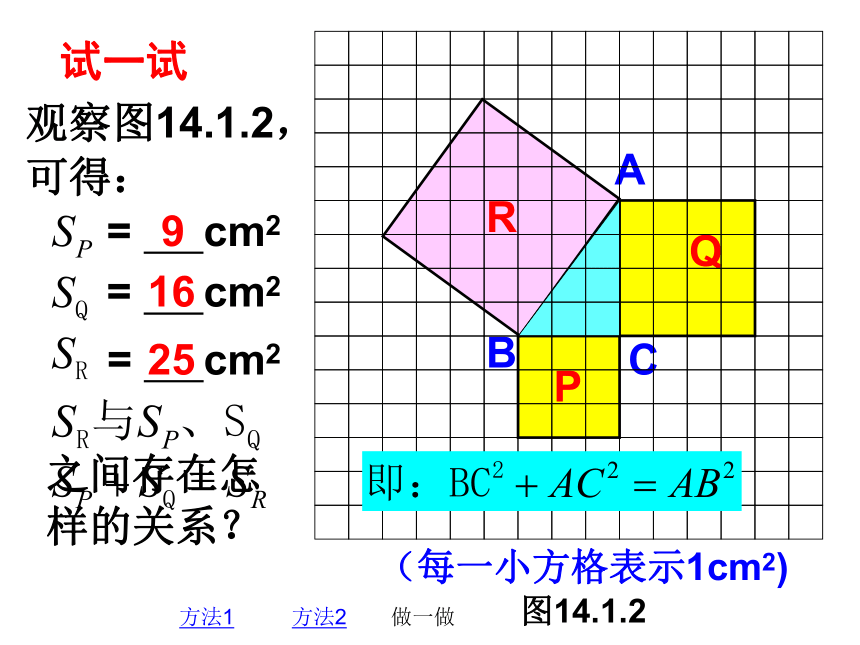
观察图14.1.2,
可得:
= cm2
= cm2
= cm2
9
16
25
之间存在怎样的关系?
方法1
方法2
做一做
A
B
C
P
Q
R
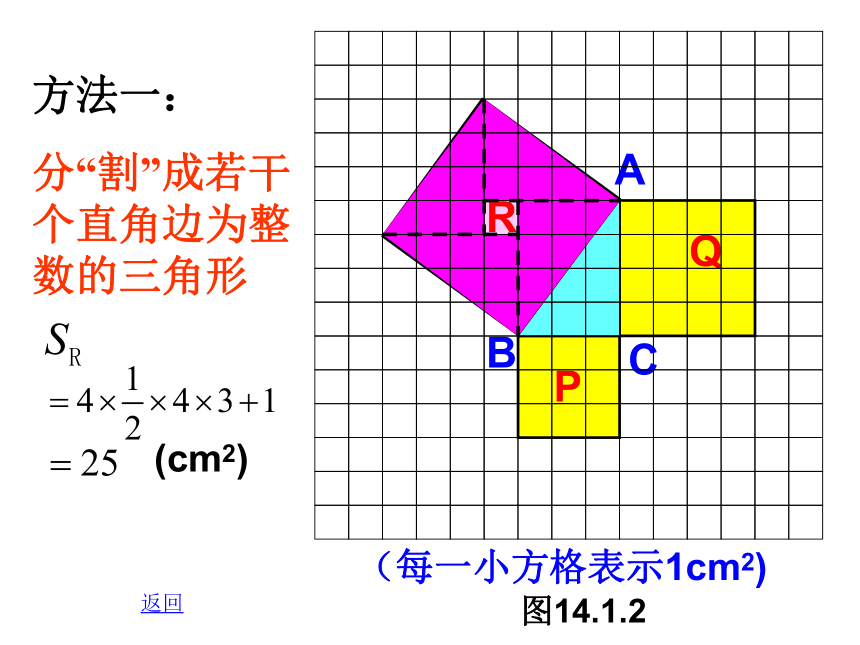
方法一:
分“割”成若干个直角边为整数的三角形
(cm2)
(每一小方格表示1cm2)
图14.1.2
返回
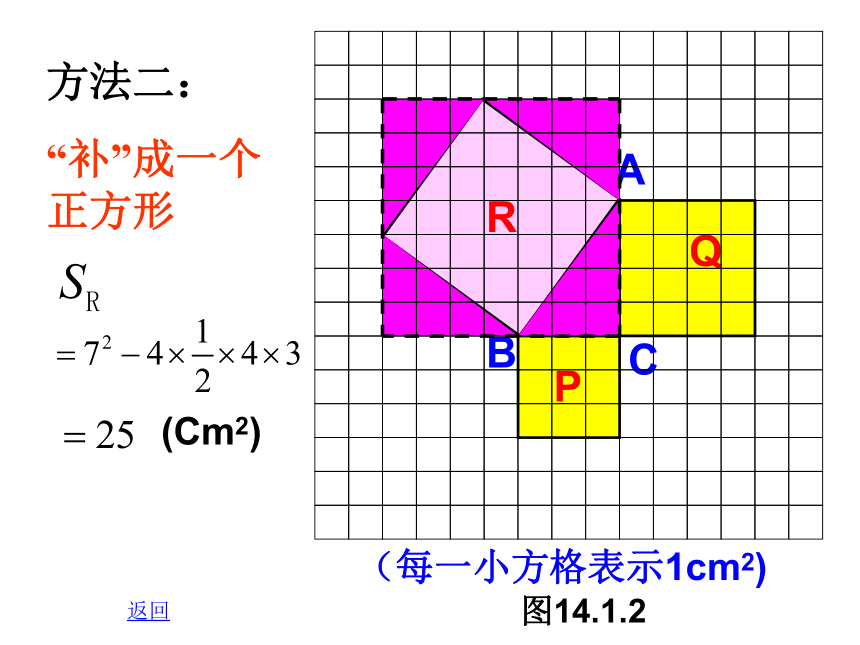
A
B
C
P
Q
R
(每一小方格表示1cm2)
图14.1.2
方法二:
“补”成一个正方形
(Cm2)
返回
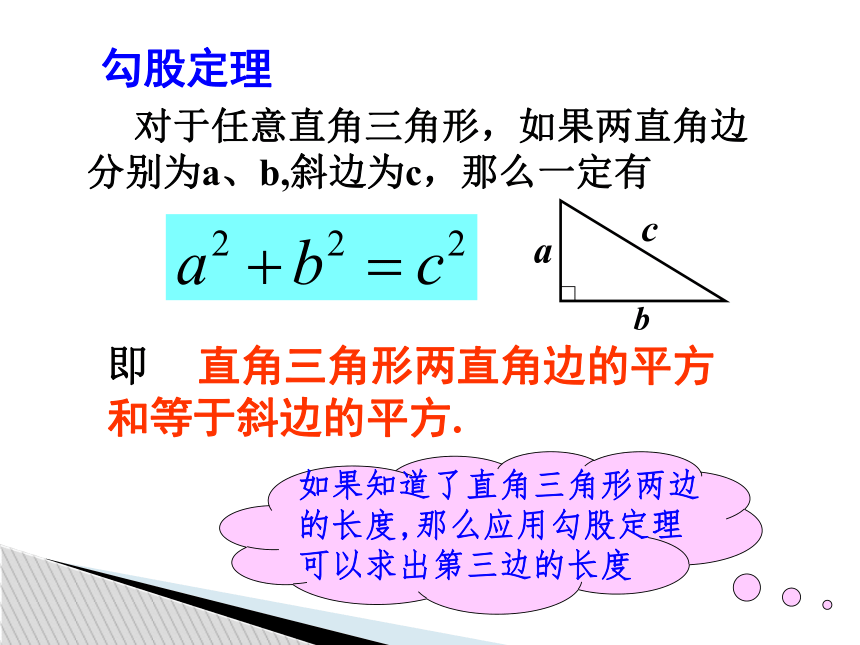
勾股定理
对于任意直角三角形,如果两直角边分别为a、b,斜边为c,那么一定有
即 直角三角形两直角边的平方和等于斜边的平方.
a
b
c
如果知道了直角三角形两边的长度,那么应用勾股定理可以求出第三边的长度
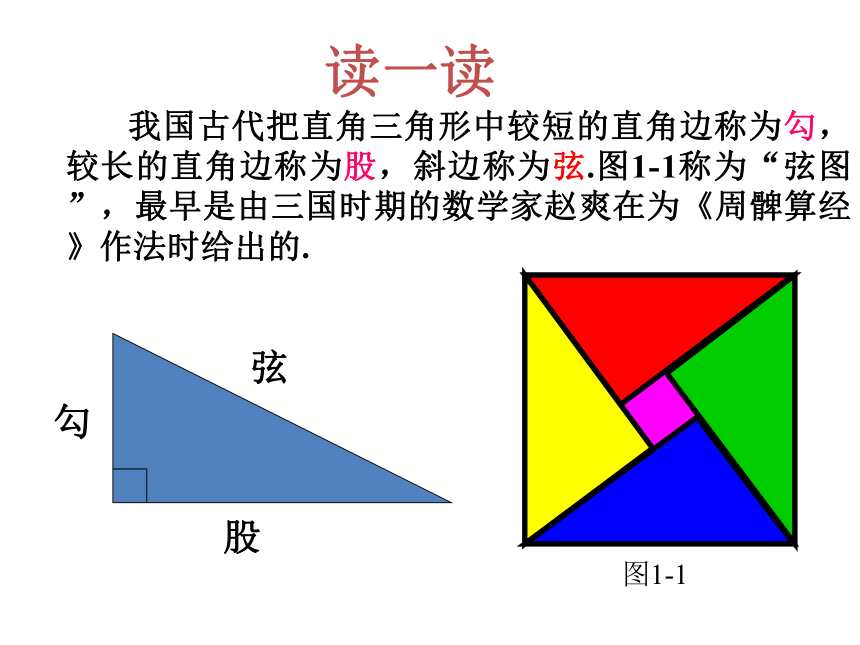
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
股
勾
图1-1
a
b
c
a
b
c
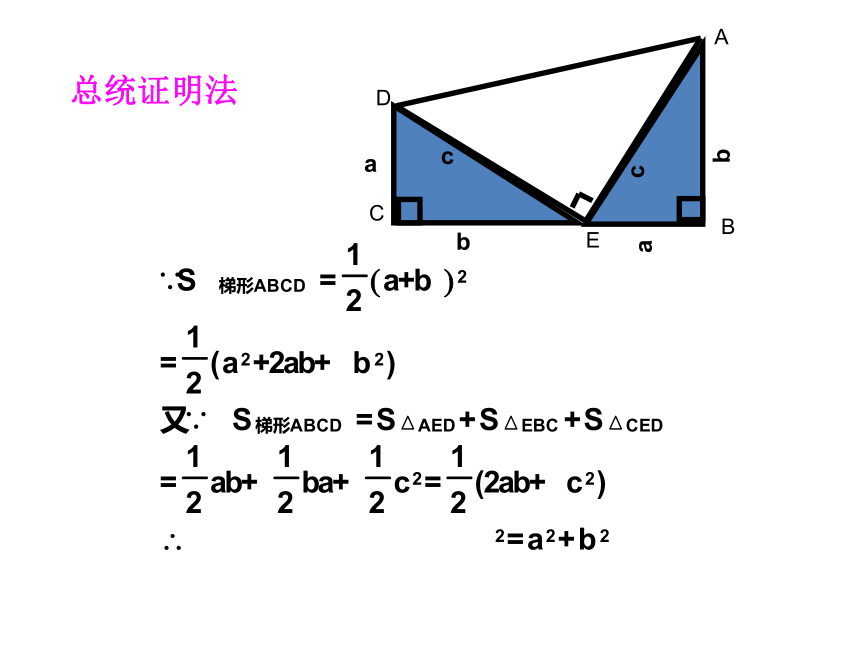
总统证明法
D
C
A
E
B
青朱出入图
a
a
b
a2+b2=c2
c
b
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
在Rt△ABC中,已知∠B=90°,
AB=6 ,BC=8,求AC
解:在Rt?ABC中,
已知AB=6 ,BC=8
A
C
B
例题讲解
6
8
=10
?
在Rt△ABC中,∠C=90°.
(1) 已知:a=3,b=4,求c;
(2) 已知:a=24,c=25,求b;
(3) 已知:c=13,b=5,求a;
试一试
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
a
b
c
C
B
A
5 或
已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
y=0
应用知识回归生活
解:由题可得
答:这棵树折断前高9米。
1.勾股定理:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
2.在直角三角形中已知两边求第三边:
课堂小结
课后练习
1、如图,为了求出位于湖两岸的两点A、 B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
如图14.1.9,在直角三角形ABC中,
AC=160米, BC=128米,
根据勾股定理可得
AB=
=
=96(米).
答: 从点A穿过湖到点B有96米.
解
2. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.
教材112页练习
3、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
比一比看看谁算得快!
4、求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
① X=15
② X=12
③ X=13
在运用勾股定理时,我们必须首先明确哪两条边是直角边,哪一条是斜边.
3、若直角三角形的三边长分别为2、 4、 x,则x=_____ .
5.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 = ____.
(2) 若 =30,且BC=5,则AB=_____
(3)若 =24,且BC=6,则AB边上的高为_____
B
A
C
24
13
4.8
试一试
1
1
数学的和谐美
勾股小常识:勾股数
1、 a?+b? =c?,满足(a,b,c)=1则a,b,c,为
基本勾股数如:3、4、5;5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、18……
3、若a,b,c是一组基本的勾股数,则a,b,c
不能同时为奇数或同时为偶数
4、一组勾股数中必有一个数是5倍数
5、2mn,m?-n?,m?+n?为勾股数组,m>n﹥0,m,n一奇一偶
直角三角形三边的关系
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
y=0
情境引入
R
Q
P
C
A
B
图14.1.1
图14.1.1是正方形瓷砖拼成的地面,观察图中画出的三个正方形P、Q、R,
之间存在怎样的关系?
观察
等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
A
B
C
P
Q
R
试一试
(每一小方格表示1cm2)
图14.1.2
观察图14.1.2,
可得:
= cm2
= cm2
= cm2
9
16
25
之间存在怎样的关系?
方法1
方法2
做一做
A
B
C
P
Q
R
方法一:
分“割”成若干个直角边为整数的三角形
(cm2)
(每一小方格表示1cm2)
图14.1.2
返回
A
B
C
P
Q
R
(每一小方格表示1cm2)
图14.1.2
方法二:
“补”成一个正方形
(Cm2)
返回
勾股定理
对于任意直角三角形,如果两直角边分别为a、b,斜边为c,那么一定有
即 直角三角形两直角边的平方和等于斜边的平方.
a
b
c
如果知道了直角三角形两边的长度,那么应用勾股定理可以求出第三边的长度
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
股
勾
图1-1
a
b
c
a
b
c
总统证明法
D
C
A
E
B
青朱出入图
a
a
b
a2+b2=c2
c
b
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
在Rt△ABC中,已知∠B=90°,
AB=6 ,BC=8,求AC
解:在Rt?ABC中,
已知AB=6 ,BC=8
A
C
B
例题讲解
6
8
=10
?
在Rt△ABC中,∠C=90°.
(1) 已知:a=3,b=4,求c;
(2) 已知:a=24,c=25,求b;
(3) 已知:c=13,b=5,求a;
试一试
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
a
b
c
C
B
A
5 或
已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
受台风威马逊的影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
y=0
应用知识回归生活
解:由题可得
答:这棵树折断前高9米。
1.勾股定理:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
2.在直角三角形中已知两边求第三边:
课堂小结
课后练习
1、如图,为了求出位于湖两岸的两点A、 B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
如图14.1.9,在直角三角形ABC中,
AC=160米, BC=128米,
根据勾股定理可得
AB=
=
=96(米).
答: 从点A穿过湖到点B有96米.
解
2. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.
教材112页练习
3、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
比一比看看谁算得快!
4、求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
① X=15
② X=12
③ X=13
在运用勾股定理时,我们必须首先明确哪两条边是直角边,哪一条是斜边.
3、若直角三角形的三边长分别为2、 4、 x,则x=_____ .
5.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 = ____.
(2) 若 =30,且BC=5,则AB=_____
(3)若 =24,且BC=6,则AB边上的高为_____
B
A
C
24
13
4.8
试一试
1
1
数学的和谐美
勾股小常识:勾股数
1、 a?+b? =c?,满足(a,b,c)=1则a,b,c,为
基本勾股数如:3、4、5;5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、18……
3、若a,b,c是一组基本的勾股数,则a,b,c
不能同时为奇数或同时为偶数
4、一组勾股数中必有一个数是5倍数
5、2mn,m?-n?,m?+n?为勾股数组,m>n﹥0,m,n一奇一偶
