冀教版初中数学八年级上册 17.2 直角三角形 课件(21张PPT)
文档属性
| 名称 | 冀教版初中数学八年级上册 17.2 直角三角形 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:25:01 | ||
图片预览








文档简介
直角三角形
1.了解直角三角形的定义及其其表示方法;
2.经历直角三角形性质的的探究过程;(难点)
3、能灵活运用直角三角形的性质解决有关问题。 (重点)
学习目标
直角三角形可以用“Rt△”表示。
Rt△ABC
A
B
C
一、直角三角形的的概念及表示方法
有一个角等于90°的三角形叫做直角三角形.
定义:
表示方法:
如图所示的三角形可以
表示为__________.
二、直角三角形的性质
1、直角三角形的角
在Rt△ABC中,关于它的两个锐角有怎样的结论?判断这个命题的真假。
写出上述命题的逆命题,并判断真假。
直角三角形的性质定理:
直角三角形的两个锐角互余.
A
B
C
直角三角形的性质定理的逆命题为:
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
直角三角形的判定定理:
完成课本149页练习
第一题 A组第一题
在一张半透明的纸上画出Rt△ABC”表示,如图所示;
A
B
C
将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE,如图所示;
A
(B)
C
E
F
将纸展开,如图所示;
A
B
C
E
F
2、直角三角形的中线
A
B
C
E
F
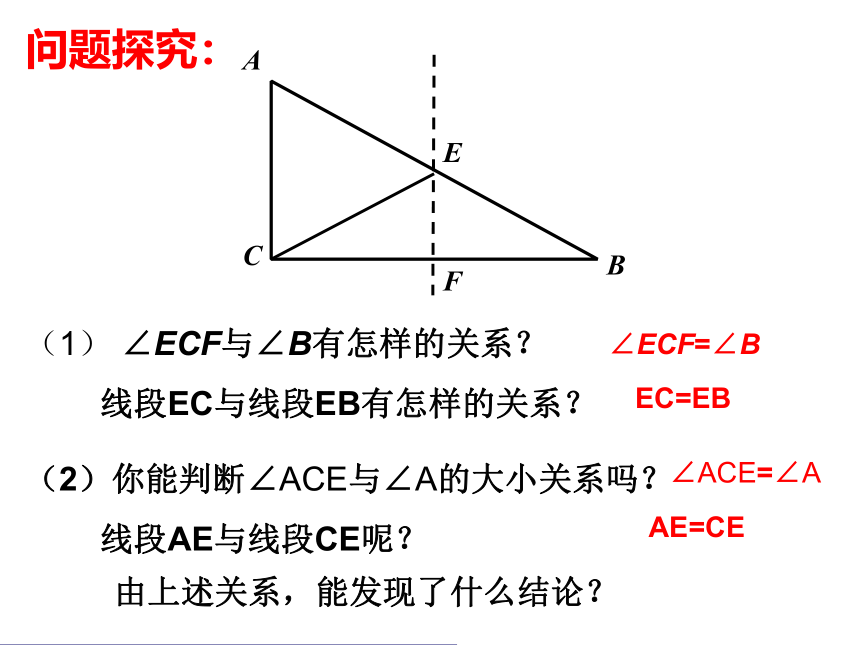
问题探究:
(1) ∠ECF与∠B有怎样的关系?
线段EC与线段EB有怎样的关系?
(2)你能判断∠ACE与∠A的大小关系吗?
线段AE与线段CE呢?
∠ECF=∠B
EC=EB
∠ACE=∠A
AE=CE
由上述关系,能发现了什么结论?
A
C
B
D
符号语言:
直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
结论:
∠ACB=90°, AD=BD
E
A
C
B
D
F
已知:如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的中线.
证明:如图,过点D作DE∥BC,交AC于点E;作DF∥AC,交BC于点F.
∵ DF∥AC(已知)
∴ ∠A=∠FDB(两直线平行,同位角相等),
∴ AD=DB(中点的定义),
∴ ∠ADE=∠B(两直线平行,同位角相等),
∵ DE∥AB(已知)
∵ D是AB的中点(已知)
在△AED和△DFB中,
∴△AED≌△DFB(SAS).
∴AE=DF,ED=FB(全等三角形对应边相等).
∵ DF∥AC(已知)
∴ ∠DCE=∠CDF(两直线平行,内错角相等),
E
A
C
B
D
F
∵ DE∥BC(已知)
∴ ∠DCE=∠CDF(两直线平行,内错角相等),
E
A
C
B
D
F
∴ △CDE≌△DCF(ASA),
∴ ED=FC,EC=FD (全等三角形对应边相等).
∴AE=EC,CF =FB(等量代换).
在△CDE和△DCF中,
∵ DF∥AC(已知)
又∵ CF =FB(已证)
∴DF为BC的垂直平分线(垂直平分线的定义)
∴ CD=BD(线段垂直平分线的性质定理)
∴AD=CD(线段垂直平分线的性质定理).
∴DE为AC的垂直平分线(垂直平分线的定义)
∵ DE∥BC(已知)
又∵ AE=EC(已证)
E
A
C
B
D
F
∴AD=CD=BD
完成课本149页
A组第二题、
B组第二题
求证:在直角三角形中,30°角所对的直角边等于斜边的一半.
做一做
A
B
C
符号语言:
完成课本149页
A组第三题
直角三角形
定义
性质
判定
有一个角等于90°的三角形
性质2:直角三角形的性质:斜边上的中线等于斜边上的一半
性质3:含30°角的直角三角形的性质:如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
课堂小结
表示方法:直角三角形可以用“Rt△”表示
性质1:直角三角形的两个锐角互余.
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
当堂练习
1.将一副三角板按照如图所示的位置放置,则两条斜边所形成的钝角α等于( )
A.120° B.135° C.150° D.165°
A
B
D
E
C
F
45°
60°
α
D
2.如图,在等腰直角三角形中,已知AB=AC,BC=10cm,AD⊥BC于点D,则AD=_____cm.
5
A
D
C
B
3.如图,在△ABC 中,∠C =90°,∠A =30°,AB =10,则BC 的长为 .
5
4.如图,在△ABC 中,∠ACB =90°,CD 是高,∠A =30°,AB =4.则BD = .
1
A
B
C
A
B
C
D
第3题
第4题
5.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC = .
5
6.如图,Rt△ABC中,∠A= 30°,AB+BC=12cm,则AB=______.
A
C
B
8
7.已知:等腰三角形的底角为15 °,腰长为20.求腰上的高.
A
C
B
D
15 °
15 °
20
解:过C作CD⊥BA交BA的延长线于点D.
∵∠B=∠ACB=15° (已知),
∴∠DAC= ∠B+ ∠ACB= 15°+15°=30°,
∴CD= AC= ×20=10.
)
)
1.了解直角三角形的定义及其其表示方法;
2.经历直角三角形性质的的探究过程;(难点)
3、能灵活运用直角三角形的性质解决有关问题。 (重点)
学习目标
直角三角形可以用“Rt△”表示。
Rt△ABC
A
B
C
一、直角三角形的的概念及表示方法
有一个角等于90°的三角形叫做直角三角形.
定义:
表示方法:
如图所示的三角形可以
表示为__________.
二、直角三角形的性质
1、直角三角形的角
在Rt△ABC中,关于它的两个锐角有怎样的结论?判断这个命题的真假。
写出上述命题的逆命题,并判断真假。
直角三角形的性质定理:
直角三角形的两个锐角互余.
A
B
C
直角三角形的性质定理的逆命题为:
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
直角三角形的判定定理:
完成课本149页练习
第一题 A组第一题
在一张半透明的纸上画出Rt△ABC”表示,如图所示;
A
B
C
将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE,如图所示;
A
(B)
C
E
F
将纸展开,如图所示;
A
B
C
E
F
2、直角三角形的中线
A
B
C
E
F
问题探究:
(1) ∠ECF与∠B有怎样的关系?
线段EC与线段EB有怎样的关系?
(2)你能判断∠ACE与∠A的大小关系吗?
线段AE与线段CE呢?
∠ECF=∠B
EC=EB
∠ACE=∠A
AE=CE
由上述关系,能发现了什么结论?
A
C
B
D
符号语言:
直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
结论:
∠ACB=90°, AD=BD
E
A
C
B
D
F
已知:如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的中线.
证明:如图,过点D作DE∥BC,交AC于点E;作DF∥AC,交BC于点F.
∵ DF∥AC(已知)
∴ ∠A=∠FDB(两直线平行,同位角相等),
∴ AD=DB(中点的定义),
∴ ∠ADE=∠B(两直线平行,同位角相等),
∵ DE∥AB(已知)
∵ D是AB的中点(已知)
在△AED和△DFB中,
∴△AED≌△DFB(SAS).
∴AE=DF,ED=FB(全等三角形对应边相等).
∵ DF∥AC(已知)
∴ ∠DCE=∠CDF(两直线平行,内错角相等),
E
A
C
B
D
F
∵ DE∥BC(已知)
∴ ∠DCE=∠CDF(两直线平行,内错角相等),
E
A
C
B
D
F
∴ △CDE≌△DCF(ASA),
∴ ED=FC,EC=FD (全等三角形对应边相等).
∴AE=EC,CF =FB(等量代换).
在△CDE和△DCF中,
∵ DF∥AC(已知)
又∵ CF =FB(已证)
∴DF为BC的垂直平分线(垂直平分线的定义)
∴ CD=BD(线段垂直平分线的性质定理)
∴AD=CD(线段垂直平分线的性质定理).
∴DE为AC的垂直平分线(垂直平分线的定义)
∵ DE∥BC(已知)
又∵ AE=EC(已证)
E
A
C
B
D
F
∴AD=CD=BD
完成课本149页
A组第二题、
B组第二题
求证:在直角三角形中,30°角所对的直角边等于斜边的一半.
做一做
A
B
C
符号语言:
完成课本149页
A组第三题
直角三角形
定义
性质
判定
有一个角等于90°的三角形
性质2:直角三角形的性质:斜边上的中线等于斜边上的一半
性质3:含30°角的直角三角形的性质:如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
课堂小结
表示方法:直角三角形可以用“Rt△”表示
性质1:直角三角形的两个锐角互余.
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
当堂练习
1.将一副三角板按照如图所示的位置放置,则两条斜边所形成的钝角α等于( )
A.120° B.135° C.150° D.165°
A
B
D
E
C
F
45°
60°
α
D
2.如图,在等腰直角三角形中,已知AB=AC,BC=10cm,AD⊥BC于点D,则AD=_____cm.
5
A
D
C
B
3.如图,在△ABC 中,∠C =90°,∠A =30°,AB =10,则BC 的长为 .
5
4.如图,在△ABC 中,∠ACB =90°,CD 是高,∠A =30°,AB =4.则BD = .
1
A
B
C
A
B
C
D
第3题
第4题
5.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC = .
5
6.如图,Rt△ABC中,∠A= 30°,AB+BC=12cm,则AB=______.
A
C
B
8
7.已知:等腰三角形的底角为15 °,腰长为20.求腰上的高.
A
C
B
D
15 °
15 °
20
解:过C作CD⊥BA交BA的延长线于点D.
∵∠B=∠ACB=15° (已知),
∴∠DAC= ∠B+ ∠ACB= 15°+15°=30°,
∴CD= AC= ×20=10.
)
)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
