人教版八年级上册第十四章 整式的乘法与因式分解 第4课时 单项式乘以单项式课件(20张PPT)
文档属性
| 名称 | 人教版八年级上册第十四章 整式的乘法与因式分解 第4课时 单项式乘以单项式课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览






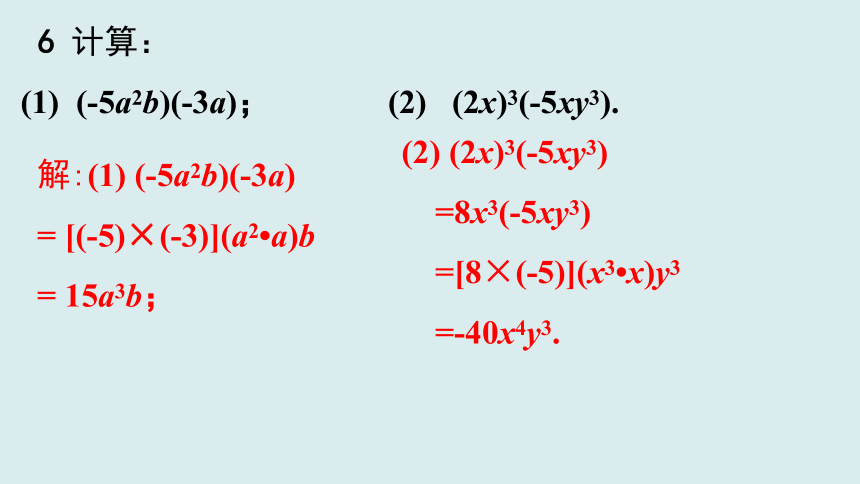
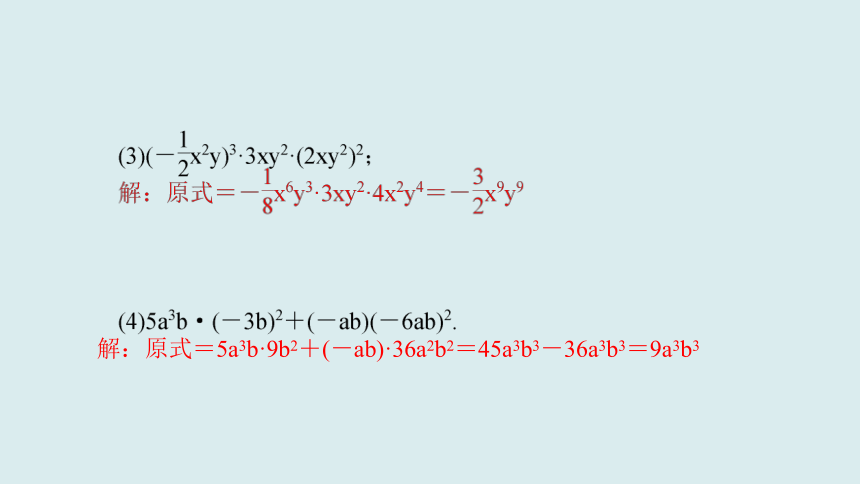

文档简介
第十四章 整式的乘法与因式分解
人教版
14.1 整式的乘法
第4课时 单项式乘以单项式
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
精彩再现
单项式与单项式的乘法法则
(1)系数相乘;
(2)相同字母的幂相乘;
( 3)其余字母连同它的指数不变,作为积的因式.
注意
单项式与单项式相乘,把它们的____、___________分别相乘,
对于只在一个单项式里含有的字母,
则连同它的指数作为________________.
系数
同底数幂
积的一个因式
知识点填空
1.计算-3a2·a3的结果为( )
A.-3a5 B.3a6 C.-3a6 D.3a5
2 下列计算正确的是( )
A.6x2·3xy=9x3y
B.(2ab2)·(-3ab)=-a2b3
C.(mn)2·(-m2n)=-m3n3
D.(-3x2y)·(-3xy)=9x3y2
A
D
3 下面计算结果对不对?如果不对,应当怎样改正?
(1)3a3 ·2a2=6a6 ( ) 改正: .
(2)3x2 ·4x2=12x2 ( ) 改正: .
(3) 5y3·3y5=15y15 ( ) 改正: .
×
×
×
3a3 ·2a2=6a5
3x2 ·4x2=12x4
5y3·3y5=15y8
4.(3分)(上海中考)计算:2a·a2=____.
5.(12分)计算:
(1)2x2y·(-4xy3z);
解:原式=[2×(-4)](x2·x)·(y·y3)·z=-8x3y4z
(2)5a2·(3a3)2;
解:原式=5a2·9a6=45a8
2a3
6 计算:
(1) (-5a2b)(-3a); (2) (2x)3(-5xy3).
解:(1) (-5a2b)(-3a)
= [(-5)×(-3)](a2?a)b
= 15a3b;
(2) (2x)3(-5xy3)
=8x3(-5xy3)
=[8×(-5)](x3?x)y3
=-40x4y3.
解:原式=5a3b·9b2+(-ab)·36a2b2=45a3b3-36a3b3=9a3b3
方法总结:
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积;
(2)注意按顺序运算;
(3)不要漏掉只在一个单项式里含有的字母因式;
(4)此性质对于多个单项式相乘仍然成立.
7.(4分)(周口月考)下列运算正确的是( )
A.(x2)3+(x3)2=2x6
B.(x2)3·(x2)3=2x12
C.x4·(2x)2=2x6
D.(2x)3·(-x)2=-8x5
A
A
1.58×106
8.(4分)如图,沿大正三角形的对称轴对折,则互相重合的两个小正三角形的单项式的乘积为_________________.
a或2a3b或2a2b
9 计算:
(1) 3x2 ·5x3 ; (2)4y ·(-2xy2);
解:(1)原式=(3×5)(x2·x3)=15x5;
(2)原式=[4×(-2)](y·y2) ·x=-8xy3;
有乘方运算,先算乘方,再算单项式相乘.
注意
针对训练
(3) (-3x)2 ·4x2 ; (4)(-2a)3(-3a)2.
(3) 原式=9x2·4x2 =(9×4)(x2·x2)=36x4;
(4)原式=-8a3·9a2 =[(-8)×9](a3·a2)=-72a5
解:原式=-10a7b7c5,当a=-5,b=0.2,c=2时,原式=320
10 已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
解:∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴m2+n=7.
解得
∴
方法总结:单项式乘以单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.
【综合运用】
11.(7分)已知(-2axby2c)(3xb-1y)=12x11y7,求a+b+c的值.
解:∵(-2axby2c)(3xb-1y)=12x11y7,∴-6ax2b-1y2c+1=12x11y7,
∴-6a=12,2b-1=11,2c+1=7,∴a=-2,b=6,c=3,
∴a+b+c=-2+6+3=7
小结
1
单项式×单项式
实质上是转化为同底数幂的运算
人教版
14.1 整式的乘法
第4课时 单项式乘以单项式
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
精彩再现
单项式与单项式的乘法法则
(1)系数相乘;
(2)相同字母的幂相乘;
( 3)其余字母连同它的指数不变,作为积的因式.
注意
单项式与单项式相乘,把它们的____、___________分别相乘,
对于只在一个单项式里含有的字母,
则连同它的指数作为________________.
系数
同底数幂
积的一个因式
知识点填空
1.计算-3a2·a3的结果为( )
A.-3a5 B.3a6 C.-3a6 D.3a5
2 下列计算正确的是( )
A.6x2·3xy=9x3y
B.(2ab2)·(-3ab)=-a2b3
C.(mn)2·(-m2n)=-m3n3
D.(-3x2y)·(-3xy)=9x3y2
A
D
3 下面计算结果对不对?如果不对,应当怎样改正?
(1)3a3 ·2a2=6a6 ( ) 改正: .
(2)3x2 ·4x2=12x2 ( ) 改正: .
(3) 5y3·3y5=15y15 ( ) 改正: .
×
×
×
3a3 ·2a2=6a5
3x2 ·4x2=12x4
5y3·3y5=15y8
4.(3分)(上海中考)计算:2a·a2=____.
5.(12分)计算:
(1)2x2y·(-4xy3z);
解:原式=[2×(-4)](x2·x)·(y·y3)·z=-8x3y4z
(2)5a2·(3a3)2;
解:原式=5a2·9a6=45a8
2a3
6 计算:
(1) (-5a2b)(-3a); (2) (2x)3(-5xy3).
解:(1) (-5a2b)(-3a)
= [(-5)×(-3)](a2?a)b
= 15a3b;
(2) (2x)3(-5xy3)
=8x3(-5xy3)
=[8×(-5)](x3?x)y3
=-40x4y3.
解:原式=5a3b·9b2+(-ab)·36a2b2=45a3b3-36a3b3=9a3b3
方法总结:
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积;
(2)注意按顺序运算;
(3)不要漏掉只在一个单项式里含有的字母因式;
(4)此性质对于多个单项式相乘仍然成立.
7.(4分)(周口月考)下列运算正确的是( )
A.(x2)3+(x3)2=2x6
B.(x2)3·(x2)3=2x12
C.x4·(2x)2=2x6
D.(2x)3·(-x)2=-8x5
A
A
1.58×106
8.(4分)如图,沿大正三角形的对称轴对折,则互相重合的两个小正三角形的单项式的乘积为_________________.
a或2a3b或2a2b
9 计算:
(1) 3x2 ·5x3 ; (2)4y ·(-2xy2);
解:(1)原式=(3×5)(x2·x3)=15x5;
(2)原式=[4×(-2)](y·y2) ·x=-8xy3;
有乘方运算,先算乘方,再算单项式相乘.
注意
针对训练
(3) (-3x)2 ·4x2 ; (4)(-2a)3(-3a)2.
(3) 原式=9x2·4x2 =(9×4)(x2·x2)=36x4;
(4)原式=-8a3·9a2 =[(-8)×9](a3·a2)=-72a5
解:原式=-10a7b7c5,当a=-5,b=0.2,c=2时,原式=320
10 已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
解:∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴m2+n=7.
解得
∴
方法总结:单项式乘以单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.
【综合运用】
11.(7分)已知(-2axby2c)(3xb-1y)=12x11y7,求a+b+c的值.
解:∵(-2axby2c)(3xb-1y)=12x11y7,∴-6ax2b-1y2c+1=12x11y7,
∴-6a=12,2b-1=11,2c+1=7,∴a=-2,b=6,c=3,
∴a+b+c=-2+6+3=7
小结
1
单项式×单项式
实质上是转化为同底数幂的运算
