人教版八年级上册第十四章 整式的乘法与因式分解14.1 第3课时 积的乘方课件(21张PPT)
文档属性
| 名称 | 人教版八年级上册第十四章 整式的乘法与因式分解14.1 第3课时 积的乘方课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 385.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:09:31 | ||
图片预览



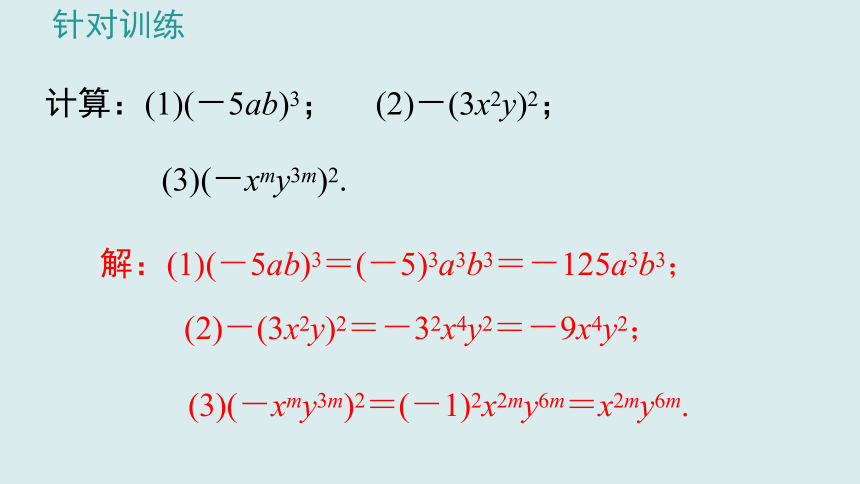




文档简介
第十四章 整式的乘法与因式分解
14.1 整式的乘法
第3课时 积的乘方
积的乘方,等于把积的每一个因式分别 ,再把所得的幂 .
(ab)n = anbn (n为正整数)
精彩再现
积的乘方法则
乘方
相乘
1.积的乘方,等于把积的_________________,
再把所得的____相乘,用字母表示为(ab)n=____.(n为正整数)
2.(abc)n=____.(n为正整数)
每一个因式分别乘方
幂
anbn
anbncn
知识点填空
计算:(1)(-5ab)3; (2)-(3x2y)2;
(3)(-xmy3m)2.
针对训练
(3)(-xmy3m)2=(-1)2x2my6m=x2my6m.
解:(1)(-5ab)3=(-5)3a3b3=-125a3b3;
(2)-(3x2y)2=-32x4y2=-9x4y2;
1.(3分)(2017·乌鲁木齐)计算(ab2)3的结果,正确的是( )
A.3ab2 B.ab6 C.a3b5 D.a3b6
2.(3分)(2017·吉林)下列计算正确的是( )
A.a2+a3=a5
B.a2·a3=a6
C.(a2)3=a6
D.(ab)2=ab2
D
C
3.(2分)(2×102)3写成科学记数法的形式为__________.
4.(3分)已知am=2,bm=3,则(ab)m=____.
8×106
6
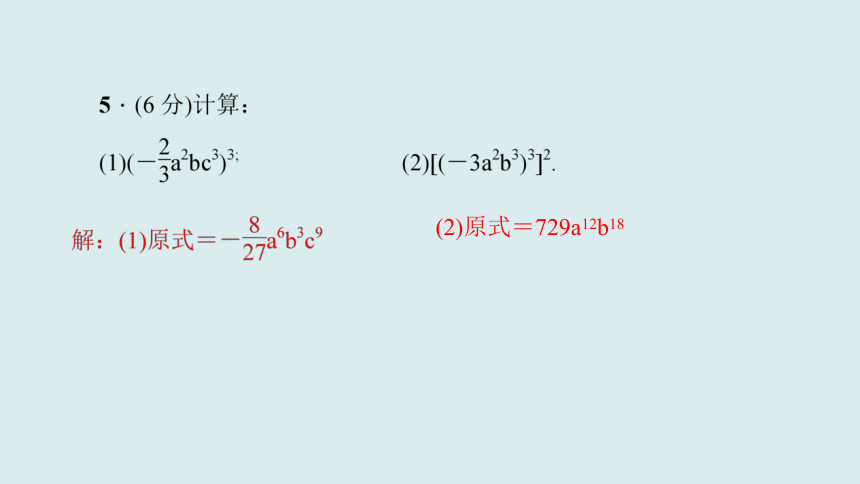
(2)原式=729a12b18
计算:
(1) -4xy2·(xy2)2·(-2x2)3;
(2) (-a3b6)2+(-a2b4)3.
解:(1)原式=-4xy2·x2y4·(-8x6)
=32x9y6;
(2)原式=a6b12+(-a6b12)
=0;
C
1
解:原式
练一练 计算:
A
D
2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2
C.(x2)3=x6 D.x2+x2=x4
C
1.计算 (-x2y)2的结果是( )
A.x4y2 B.-x4y2
C.x2y2 D.-x2y2
A
10.(4分)(1)若n为正整数,且x2n=3,则(3x3n)2=____;
(2)若(x3)5=215×315,则x=____.
11.(3分)现规定运算@ 的意义为a@b =(ab)b,
例如3@ 2=(3×2)2=36,则x@3=____.
243
6
27x3
计算:(1) 82016×0.1252015= ________;
(2) ______;
(3) (0.04)2013×[(-5)2013]2=________.
8
-3
1
12.(6分)计算:
(1)x·x5+(-2x2)2·x2+(-2x2)3;
解:原式=x6+4x4·x2-8x6=x6+4x6-8x6=-3x6
(2)0.042 018×(52 019)2.
解:原式=0.042 018×(52)2 018×52=(0.04×25)2 018×52=25
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9
= 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
计算:
如何简便计算(0.04)2004×[(-5)2004]2?
议一议
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
=14008
(0.04)2004×[(-5)2004]2
=1.
解法一:
=(0.04)2004 × [(-5)2]2004
=(0.04×25)2004
=12004
=1.
= (0.04)2004 ×(25)2004
(0.04)2004×[(-5)2004]2
解法二:
【综合运用】
.(8分)(1)已知xn=2,yn=3,求(x2y)2n的值;
解:(x2y)2n=x4n·y2n=(xn)4·(yn)2=24×32=16×9=144
(2)已知2x+3·3x+3=62x-4,求x的值.
解:∵2x+3·3x+3=6x+3=62x-4,∴x+3=2x-4,∴x=7
拓展提升:
如果(an?bm?b)3=a9b15,求m, n的值.
? (an)3?(bm)3?b3=a9b15,
? a 3n ?b 3m?b3=a9b15 ,
? a 3n ?b 3m+3=a9b15,
? 3n=9 ,3m+3=15.
?n=3,m=4.
解:∵(an?bm?b)3=a9b15,
14.1 整式的乘法
第3课时 积的乘方
积的乘方,等于把积的每一个因式分别 ,再把所得的幂 .
(ab)n = anbn (n为正整数)
精彩再现
积的乘方法则
乘方
相乘
1.积的乘方,等于把积的_________________,
再把所得的____相乘,用字母表示为(ab)n=____.(n为正整数)
2.(abc)n=____.(n为正整数)
每一个因式分别乘方
幂
anbn
anbncn
知识点填空
计算:(1)(-5ab)3; (2)-(3x2y)2;
(3)(-xmy3m)2.
针对训练
(3)(-xmy3m)2=(-1)2x2my6m=x2my6m.
解:(1)(-5ab)3=(-5)3a3b3=-125a3b3;
(2)-(3x2y)2=-32x4y2=-9x4y2;
1.(3分)(2017·乌鲁木齐)计算(ab2)3的结果,正确的是( )
A.3ab2 B.ab6 C.a3b5 D.a3b6
2.(3分)(2017·吉林)下列计算正确的是( )
A.a2+a3=a5
B.a2·a3=a6
C.(a2)3=a6
D.(ab)2=ab2
D
C
3.(2分)(2×102)3写成科学记数法的形式为__________.
4.(3分)已知am=2,bm=3,则(ab)m=____.
8×106
6
(2)原式=729a12b18
计算:
(1) -4xy2·(xy2)2·(-2x2)3;
(2) (-a3b6)2+(-a2b4)3.
解:(1)原式=-4xy2·x2y4·(-8x6)
=32x9y6;
(2)原式=a6b12+(-a6b12)
=0;
C
1
解:原式
练一练 计算:
A
D
2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2
C.(x2)3=x6 D.x2+x2=x4
C
1.计算 (-x2y)2的结果是( )
A.x4y2 B.-x4y2
C.x2y2 D.-x2y2
A
10.(4分)(1)若n为正整数,且x2n=3,则(3x3n)2=____;
(2)若(x3)5=215×315,则x=____.
11.(3分)现规定运算@ 的意义为a@b =(ab)b,
例如3@ 2=(3×2)2=36,则x@3=____.
243
6
27x3
计算:(1) 82016×0.1252015= ________;
(2) ______;
(3) (0.04)2013×[(-5)2013]2=________.
8
-3
1
12.(6分)计算:
(1)x·x5+(-2x2)2·x2+(-2x2)3;
解:原式=x6+4x4·x2-8x6=x6+4x6-8x6=-3x6
(2)0.042 018×(52 019)2.
解:原式=0.042 018×(52)2 018×52=(0.04×25)2 018×52=25
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9
= 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
计算:
如何简便计算(0.04)2004×[(-5)2004]2?
议一议
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
=14008
(0.04)2004×[(-5)2004]2
=1.
解法一:
=(0.04)2004 × [(-5)2]2004
=(0.04×25)2004
=12004
=1.
= (0.04)2004 ×(25)2004
(0.04)2004×[(-5)2004]2
解法二:
【综合运用】
.(8分)(1)已知xn=2,yn=3,求(x2y)2n的值;
解:(x2y)2n=x4n·y2n=(xn)4·(yn)2=24×32=16×9=144
(2)已知2x+3·3x+3=62x-4,求x的值.
解:∵2x+3·3x+3=6x+3=62x-4,∴x+3=2x-4,∴x=7
拓展提升:
如果(an?bm?b)3=a9b15,求m, n的值.
? (an)3?(bm)3?b3=a9b15,
? a 3n ?b 3m?b3=a9b15 ,
? a 3n ?b 3m+3=a9b15,
? 3n=9 ,3m+3=15.
?n=3,m=4.
解:∵(an?bm?b)3=a9b15,
