人教版九年级数学下册 28.1 锐角三角函数课件(共16张PPT)
文档属性
| 名称 | 人教版九年级数学下册 28.1 锐角三角函数课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:32:47 | ||
图片预览





文档简介
28.1锐角三角函数
30°、45°、60°角的三角函数值及其有关运算
人教版九年级数学下册
三角王国比一比
情景导入
90° 45° 45°
90° 30° 60°
三角函数
A
B
C
对边
斜边
邻边
斜边
正弦:SinA=
余弦:CosA=
正切:tanA=
对边
邻边
都是边的比
新课探究
已知:在Rt△ABC中,∠B=90°,∠A=30°,∠C=60°
求:Rt△ABC中的锐角三角函数值。
SinA=
A
B
C
∠A和∠C
分析:
1、Rt△ABC的锐角有几个?分别是谁?
2、锐角三角函数值是什么?
AB
AC
CosC=
AB
BC
tanC=
BC
AC
SinC=
BC
AC
CosA=
BC
AB
tanA=
AB
AC
解:
正弦、余弦、正切
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm,
求:Rt△ABC中∠A的三角函数值。
SinA=Sin30°=
A
C
B
CosA=
BC
AB
tanA=
解:
=
2
4
2cm
4cm
=
1
2
Cos30°=
AC
AB
30°
=
4
=
2
tan30°=
=
60°
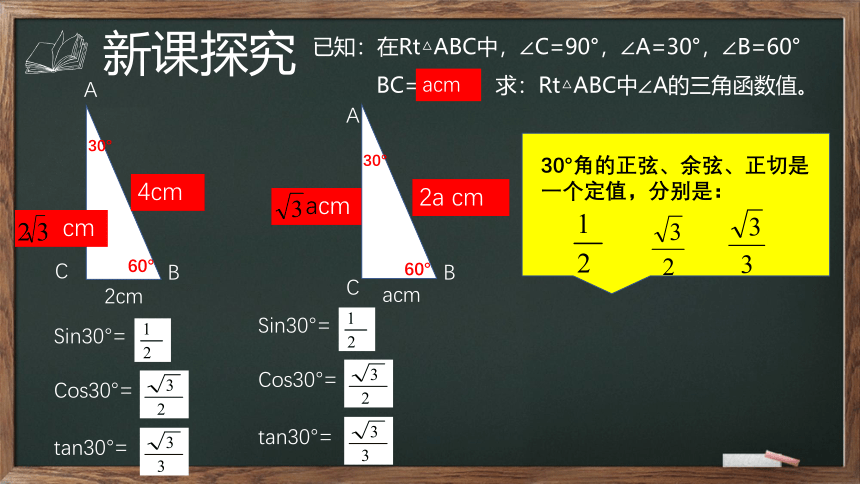
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm 求:Rt△ABC中∠A的三角函数值。
A
C
B
2cm
4cm
30°
Sin30°=
Cos30°=
tan30°=
cm
acm
2a cm
acm
Sin30°=
Cos30°=
tan30°=
30°角的正弦、余弦、正切是一个定值,分别是:
B
acm
A
C
30°
60°
60°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm,
求:Rt△ABC中∠B的三角函数值。
SinB=Sin60°=
A
C
B
AC
AB
解:
2cm
4cm
60°
4
=
=
2
tanB=
tan60°=
=
=
1
2
CosB=
Cos60°=
BC
AB
30°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm 求:Rt△ABC中∠B的三角函数值。
A
C
B
2cm
4cm
30°
Sin60°=
Cos60°=
tan30°=
cm
acm
2a cm
acm
Sin60°=
Cos60°=
tan60°=
60°角的正弦、余弦、正切是一个定值,分别是:
A
C
B
acm
30°
60°
60°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=45°,∠B=45°
BC=acm,
求:Rt△ABC中∠A和∠B的三角函数值。(分小组完成)
A
C
B
解:
acm
45°
45°
tanA=tan45°=
CosA=Cos45°=
SinA=Sin45°=
tanB=tan45°=
CosB=Cos45°=
SinB=Sin45°=
发现:
观察表格中的数据,你发现了什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A
30°
45°
60°
SinA
CosA
tanA
1随着角的增大,函数值怎样变化?
2、∠A与∠B之间有怎样的关系?
3、∠A与∠B的函数值又有怎样的关系?
结论:
1.30°、45°、60°角的三角函数值是一个定值。
2. 对于sinα与tanα,角度越大,函数值就越大;
对于cosα,角度越大,函数值就越小.
3. 当A,B均为锐角时,
若A≠B,则sinA ≠ sinB,cosA ≠ cosB,tanA ≠ tanB
4. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA = cosB,cosA = sinB tanA · tanB =1 .
例题精炼:
例:求下列各式的值。
(1)Sin30°+Cos60°
(2)3+Sin45°
(3)
解:
解:
解:
练一练
B
A
A
1、特殊值的三角函数值我们是如何推导的?
2、特殊角的三角函数值是多少?
3、在进行特殊角的三角函数值计算时我们应
该注意些什么?
体会 分享
下节课再见!
30°、45°、60°角的三角函数值及其有关运算
人教版九年级数学下册
三角王国比一比
情景导入
90° 45° 45°
90° 30° 60°
三角函数
A
B
C
对边
斜边
邻边
斜边
正弦:SinA=
余弦:CosA=
正切:tanA=
对边
邻边
都是边的比
新课探究
已知:在Rt△ABC中,∠B=90°,∠A=30°,∠C=60°
求:Rt△ABC中的锐角三角函数值。
SinA=
A
B
C
∠A和∠C
分析:
1、Rt△ABC的锐角有几个?分别是谁?
2、锐角三角函数值是什么?
AB
AC
CosC=
AB
BC
tanC=
BC
AC
SinC=
BC
AC
CosA=
BC
AB
tanA=
AB
AC
解:
正弦、余弦、正切
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm,
求:Rt△ABC中∠A的三角函数值。
SinA=Sin30°=
A
C
B
CosA=
BC
AB
tanA=
解:
=
2
4
2cm
4cm
=
1
2
Cos30°=
AC
AB
30°
=
4
=
2
tan30°=
=
60°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm 求:Rt△ABC中∠A的三角函数值。
A
C
B
2cm
4cm
30°
Sin30°=
Cos30°=
tan30°=
cm
acm
2a cm
acm
Sin30°=
Cos30°=
tan30°=
30°角的正弦、余弦、正切是一个定值,分别是:
B
acm
A
C
30°
60°
60°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm,
求:Rt△ABC中∠B的三角函数值。
SinB=Sin60°=
A
C
B
AC
AB
解:
2cm
4cm
60°
4
=
=
2
tanB=
tan60°=
=
=
1
2
CosB=
Cos60°=
BC
AB
30°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°
BC=2cm 求:Rt△ABC中∠B的三角函数值。
A
C
B
2cm
4cm
30°
Sin60°=
Cos60°=
tan30°=
cm
acm
2a cm
acm
Sin60°=
Cos60°=
tan60°=
60°角的正弦、余弦、正切是一个定值,分别是:
A
C
B
acm
30°
60°
60°
新课探究
已知:在Rt△ABC中,∠C=90°,∠A=45°,∠B=45°
BC=acm,
求:Rt△ABC中∠A和∠B的三角函数值。(分小组完成)
A
C
B
解:
acm
45°
45°
tanA=tan45°=
CosA=Cos45°=
SinA=Sin45°=
tanB=tan45°=
CosB=Cos45°=
SinB=Sin45°=
发现:
观察表格中的数据,你发现了什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A
30°
45°
60°
SinA
CosA
tanA
1随着角的增大,函数值怎样变化?
2、∠A与∠B之间有怎样的关系?
3、∠A与∠B的函数值又有怎样的关系?
结论:
1.30°、45°、60°角的三角函数值是一个定值。
2. 对于sinα与tanα,角度越大,函数值就越大;
对于cosα,角度越大,函数值就越小.
3. 当A,B均为锐角时,
若A≠B,则sinA ≠ sinB,cosA ≠ cosB,tanA ≠ tanB
4. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA = cosB,cosA = sinB tanA · tanB =1 .
例题精炼:
例:求下列各式的值。
(1)Sin30°+Cos60°
(2)3+Sin45°
(3)
解:
解:
解:
练一练
B
A
A
1、特殊值的三角函数值我们是如何推导的?
2、特殊角的三角函数值是多少?
3、在进行特殊角的三角函数值计算时我们应
该注意些什么?
体会 分享
下节课再见!
