人教版数学九年级上册 21.2.3因式分解法 课件(共20张PPT)
文档属性
| 名称 | 人教版数学九年级上册 21.2.3因式分解法 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 18:49:30 | ||
图片预览



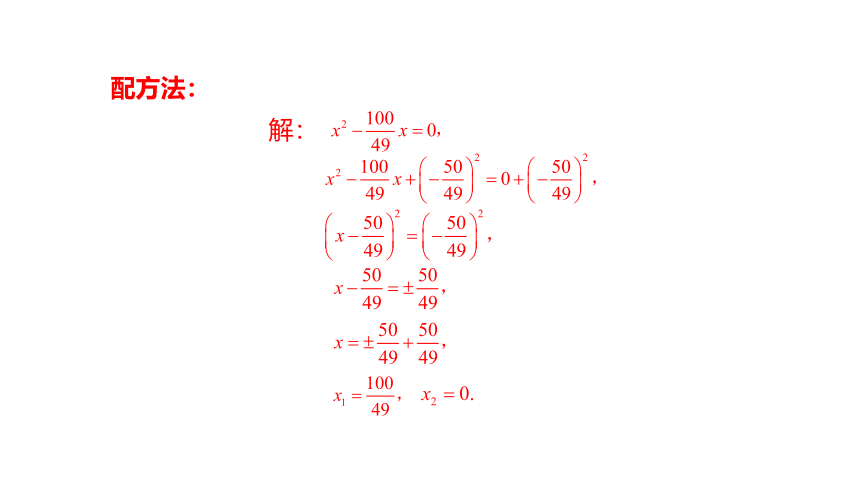




文档简介
人教版数学九年级上册
第二十一章 二元一次方程
21.2.3 因式分解法
平方差公式解方程
学习目标
1.掌握一元二次方程的四种解法,会根据方程的不同特点,灵活选用适当的方法求解方程。
2.方程求解过程中注重方式、方法的引导,特殊到一般、字母表示数、整体代入等数学思想方法的渗透。
3.培养概括、归纳总结能力,通过揭示各种解法的本质联系,渗透降次化归的思想方法。
同学们,请你们分别用配方法、公式法和因式分解法解方程 10x-4.9x2=0。
导入新知
解:
配方法:
解:
∵ a=4.9,b=-10,c=0.
∴ b2-4ac= (-10)2-4×4.9×0=100.
公式法:
10x-4.9x2=0转化为一般式为4.9x2-10x=0.
解:
因式分解法:
或
10x-4.9x2=0
x(10-4.9x) =0
x =0
10-4.9x=0
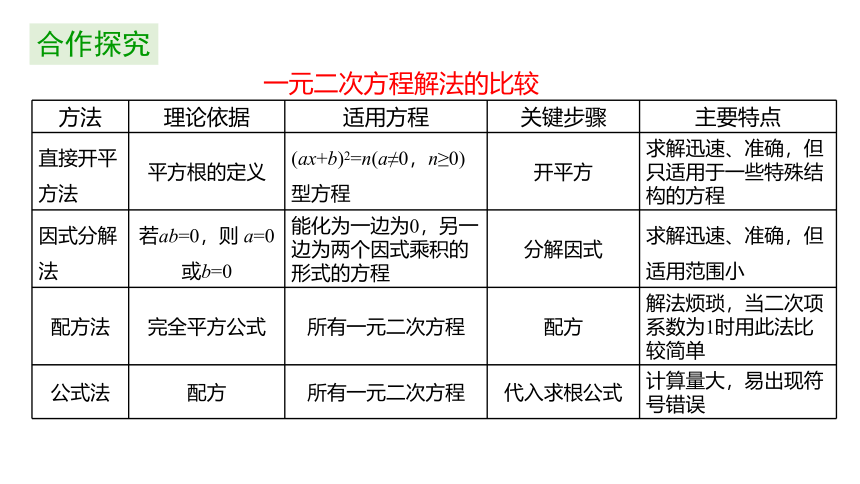
一元二次方程解法的比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法
理论依据
适用方程
关键步骤
主要特点
直接开平方法
平方根的定义
(ax+b)2=n(a≠0,n≥0)型方程
开平方
求解迅速、准确,但只适用于一些特殊结构的方程
因式分解法
若ab=0,则 a=0或b=0
能化为一边为0,另一边为两个因式乘积的形式的方程
分解因式
求解迅速、准确,但适用范围小
配方法
完全平方公式
所有一元二次方程
配方
解法烦琐,当二次项系数为1时用此法比较简单
公式法
配方
所有一元二次方程
代入求根公式
计算量大,易出现符号错误
合作探究
例 用适当的方法解下列方程:
(1) x2-2x-8=0;(2) 2x2-7x+6=0;(3) (x-1)2-2x+2=0.
解:(1)移项,得 x2-2x=8,
配方,得(x-1)2=9,
所以x-1=±3,
所以x1=4,x2=-2.
例 用适当的方法解下列方程:
(1) x2-2x-8=0;(2) 2x2-7x+6=0;(3) (x-1)2-2x+2=0.
?
例 用适当的方法解下列方程:
(1) x2-2x-8=0;(2) 2x2-7x+6=0;(3) (x-1)2-2x+2=0.
解:(3)原方程可化为 (x-1)2-2(x-1)=0,
因式分解,得 (x-1)(x-1-2)=0,
所以 x-1=0或 x-3=0,
所以 x1=1,x2=3.
解一元二次方程的方法的选择技巧
若一元二次方程可化为 (mx+n)2=p(m≠0,p≥0) 的形式,则宜选用直接开平方法;若一元二次方程的二次项系数为 1,一次项系数为偶数,则宜选用配方法;若一元二次方程整理后右边为 0,且左边能进行因式分解,则宜选用因式分解法;若直接开平方法、配方法、因式分解法都不简便,则宜选用公式法。
技巧点拨
解一元二次方程方法的口诀
方程没有一次项,直接开方最理想,
如果缺少常数项,因式分解没商量,
b,c 相等都为 0,等根是 0 不要忘,
b,c 同时不为 0,因式分解或配方,
也可直接套公式,因题而异择良方.
合作探究
1.用适当的方法解方程:
(1) 3x(x + 5)= 5(x + 5); (2) (5x + 1)2=1;
?
?
典型例题
(3)x2 - 12x = 4 ; (4)3x2 = 4x + 1.
?
分析:二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
解:化为一般形式 3x2 -4x-1=0.
∵Δ=b2 - 4ac = 28 > 0,
2.用适当的方法解方程:
① x2-3x+1=0 ; ② 3x2-1=0 ;
③ -3t2+t=0 ; ④ x2-4x=2 ;
⑤ 2x2-x=0; ⑥ 5(m+2)2=8;
⑦ 3y2-y-1=0; ⑧ 2x2+4x-1=0;
⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
1.填空:
⑥
①
②
③
④
⑤
⑦
⑧
⑨
课堂练习
解:化为一般式为
因式分解,得
x2-2x+1 = 0.
( x-1 )( x-1 ) = 0.
有 x - 1 = 0 或 x - 1 = 0,
所以x1=x2=1.
解:因式分解,得
( 2x + 11 )( 2x- 11 ) = 0.
有 2x + 11 = 0 或 2x - 11= 0,
2.解方程:
(1) 3x2-6x=-3; (2) 4x2-121=0.
所以
1.解方程 (5x-1)2=3(5x-1) 的最适当的方法是( )
D
A.直接开平方法
B.配方法
C.公式法
D.因式分解法
中考实题
2.用合适的方法解下列一元二次方程:
(1) 4(1-x)2=9; (2) x2+2x+4=2x2+2;
?
?
3.用合适的方法解下列一元二次方程:
(3) 3x2-2x-2=0; (4) 2y2+4y=y+2.
?
?
再 见
第二十一章 二元一次方程
21.2.3 因式分解法
平方差公式解方程
学习目标
1.掌握一元二次方程的四种解法,会根据方程的不同特点,灵活选用适当的方法求解方程。
2.方程求解过程中注重方式、方法的引导,特殊到一般、字母表示数、整体代入等数学思想方法的渗透。
3.培养概括、归纳总结能力,通过揭示各种解法的本质联系,渗透降次化归的思想方法。
同学们,请你们分别用配方法、公式法和因式分解法解方程 10x-4.9x2=0。
导入新知
解:
配方法:
解:
∵ a=4.9,b=-10,c=0.
∴ b2-4ac= (-10)2-4×4.9×0=100.
公式法:
10x-4.9x2=0转化为一般式为4.9x2-10x=0.
解:
因式分解法:
或
10x-4.9x2=0
x(10-4.9x) =0
x =0
10-4.9x=0
一元二次方程解法的比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法
理论依据
适用方程
关键步骤
主要特点
直接开平方法
平方根的定义
(ax+b)2=n(a≠0,n≥0)型方程
开平方
求解迅速、准确,但只适用于一些特殊结构的方程
因式分解法
若ab=0,则 a=0或b=0
能化为一边为0,另一边为两个因式乘积的形式的方程
分解因式
求解迅速、准确,但适用范围小
配方法
完全平方公式
所有一元二次方程
配方
解法烦琐,当二次项系数为1时用此法比较简单
公式法
配方
所有一元二次方程
代入求根公式
计算量大,易出现符号错误
合作探究
例 用适当的方法解下列方程:
(1) x2-2x-8=0;(2) 2x2-7x+6=0;(3) (x-1)2-2x+2=0.
解:(1)移项,得 x2-2x=8,
配方,得(x-1)2=9,
所以x-1=±3,
所以x1=4,x2=-2.
例 用适当的方法解下列方程:
(1) x2-2x-8=0;(2) 2x2-7x+6=0;(3) (x-1)2-2x+2=0.
?
例 用适当的方法解下列方程:
(1) x2-2x-8=0;(2) 2x2-7x+6=0;(3) (x-1)2-2x+2=0.
解:(3)原方程可化为 (x-1)2-2(x-1)=0,
因式分解,得 (x-1)(x-1-2)=0,
所以 x-1=0或 x-3=0,
所以 x1=1,x2=3.
解一元二次方程的方法的选择技巧
若一元二次方程可化为 (mx+n)2=p(m≠0,p≥0) 的形式,则宜选用直接开平方法;若一元二次方程的二次项系数为 1,一次项系数为偶数,则宜选用配方法;若一元二次方程整理后右边为 0,且左边能进行因式分解,则宜选用因式分解法;若直接开平方法、配方法、因式分解法都不简便,则宜选用公式法。
技巧点拨
解一元二次方程方法的口诀
方程没有一次项,直接开方最理想,
如果缺少常数项,因式分解没商量,
b,c 相等都为 0,等根是 0 不要忘,
b,c 同时不为 0,因式分解或配方,
也可直接套公式,因题而异择良方.
合作探究
1.用适当的方法解方程:
(1) 3x(x + 5)= 5(x + 5); (2) (5x + 1)2=1;
?
?
典型例题
(3)x2 - 12x = 4 ; (4)3x2 = 4x + 1.
?
分析:二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
解:化为一般形式 3x2 -4x-1=0.
∵Δ=b2 - 4ac = 28 > 0,
2.用适当的方法解方程:
① x2-3x+1=0 ; ② 3x2-1=0 ;
③ -3t2+t=0 ; ④ x2-4x=2 ;
⑤ 2x2-x=0; ⑥ 5(m+2)2=8;
⑦ 3y2-y-1=0; ⑧ 2x2+4x-1=0;
⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
1.填空:
⑥
①
②
③
④
⑤
⑦
⑧
⑨
课堂练习
解:化为一般式为
因式分解,得
x2-2x+1 = 0.
( x-1 )( x-1 ) = 0.
有 x - 1 = 0 或 x - 1 = 0,
所以x1=x2=1.
解:因式分解,得
( 2x + 11 )( 2x- 11 ) = 0.
有 2x + 11 = 0 或 2x - 11= 0,
2.解方程:
(1) 3x2-6x=-3; (2) 4x2-121=0.
所以
1.解方程 (5x-1)2=3(5x-1) 的最适当的方法是( )
D
A.直接开平方法
B.配方法
C.公式法
D.因式分解法
中考实题
2.用合适的方法解下列一元二次方程:
(1) 4(1-x)2=9; (2) x2+2x+4=2x2+2;
?
?
3.用合适的方法解下列一元二次方程:
(3) 3x2-2x-2=0; (4) 2y2+4y=y+2.
?
?
再 见
同课章节目录
