人教版数学九年级上册 24.1.1圆课件(共26张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.1.1圆课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 975.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览



文档简介
24.1.1
圆
.
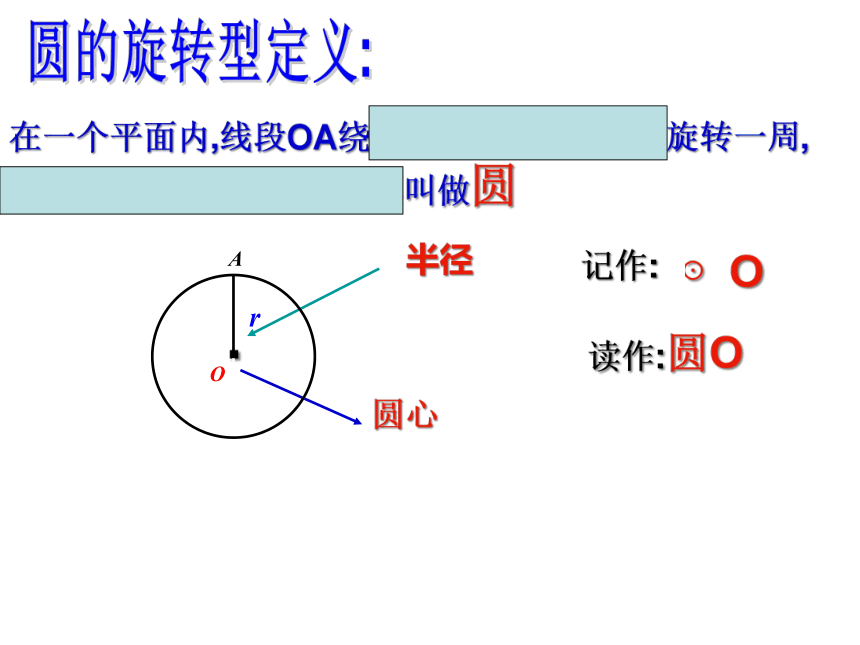
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆
圆心
半径
记作:
读作:圆O
⊙
O
·
r
O
A
O
A
r
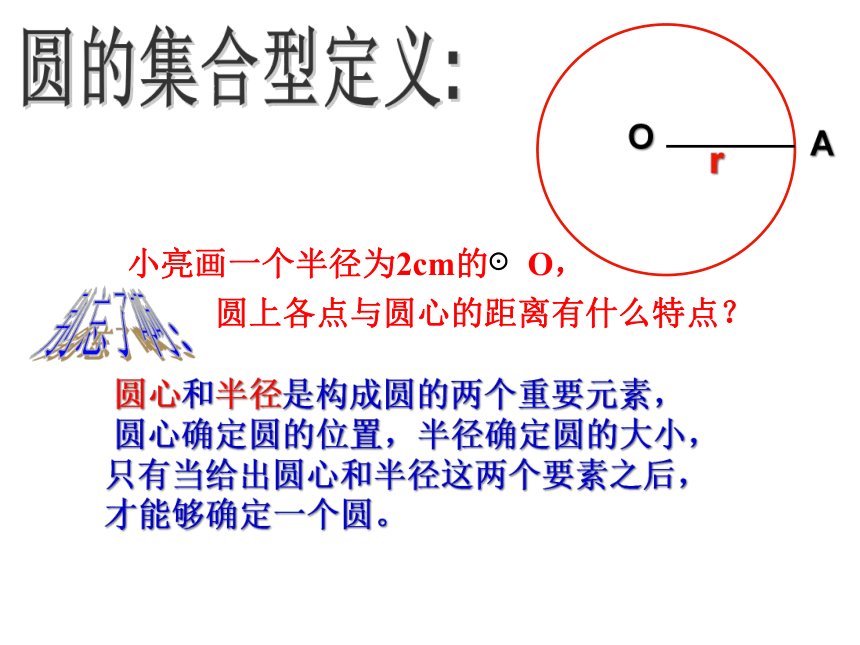
圆心和半径是构成圆的两个重要元素,
圆心确定圆的位置,半径确定圆的大小,
只有当给出圆心和半径这两个要素之后,
才能够确定一个圆。
小亮画一个半径为2cm的⊙O,
圆上各点与圆心的距离有什么特点?
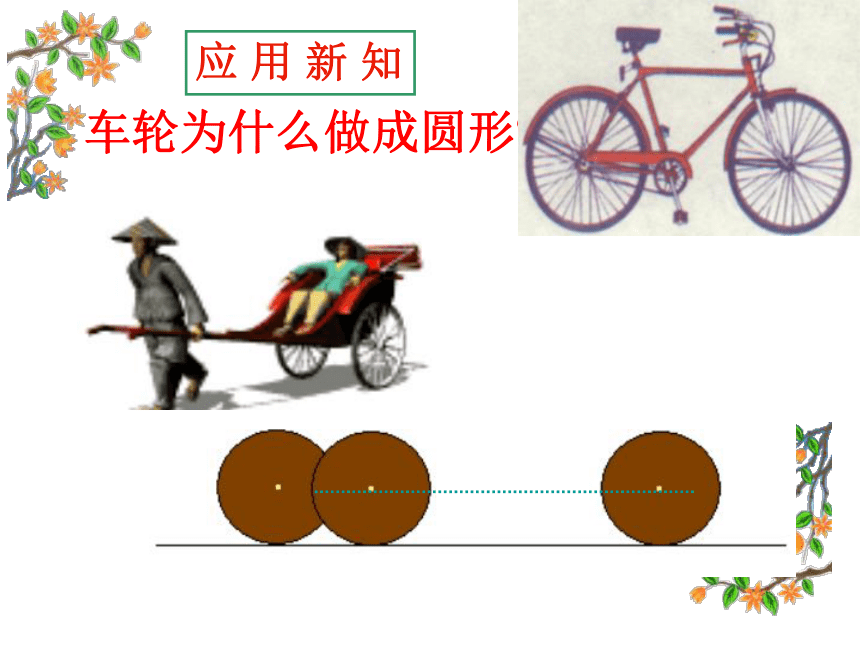
车轮为什么做成圆形?
应 用 新 知
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
议一议
为什么车轮是圆的呢?椭圆或正方形可以吗
.
O
A
B
C
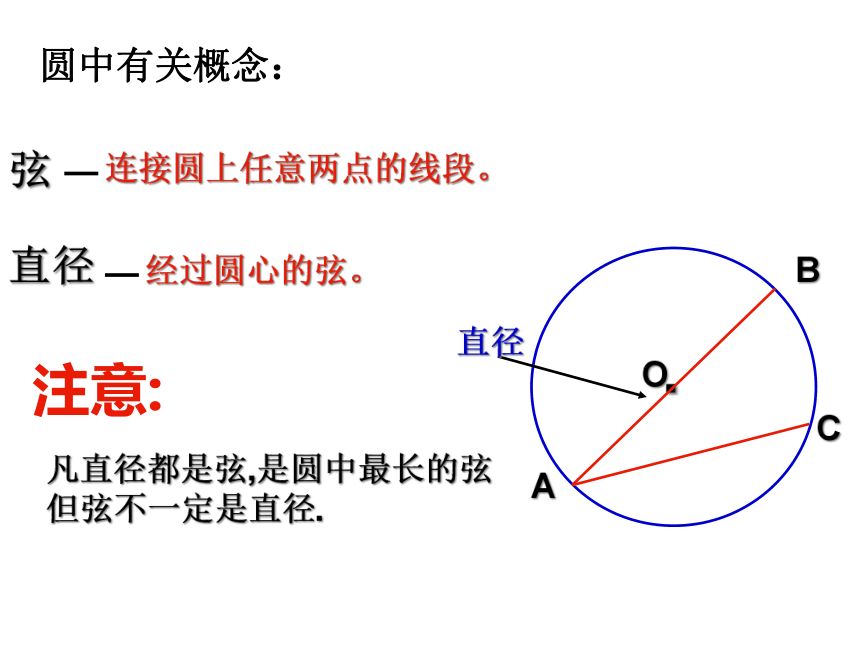
弦
连接圆上任意两点的线段。
直径
经过圆心的弦。
直径
注意:
凡直径都是弦,是圆中最长的弦
但弦不一定是直径.
圆中有关概念:
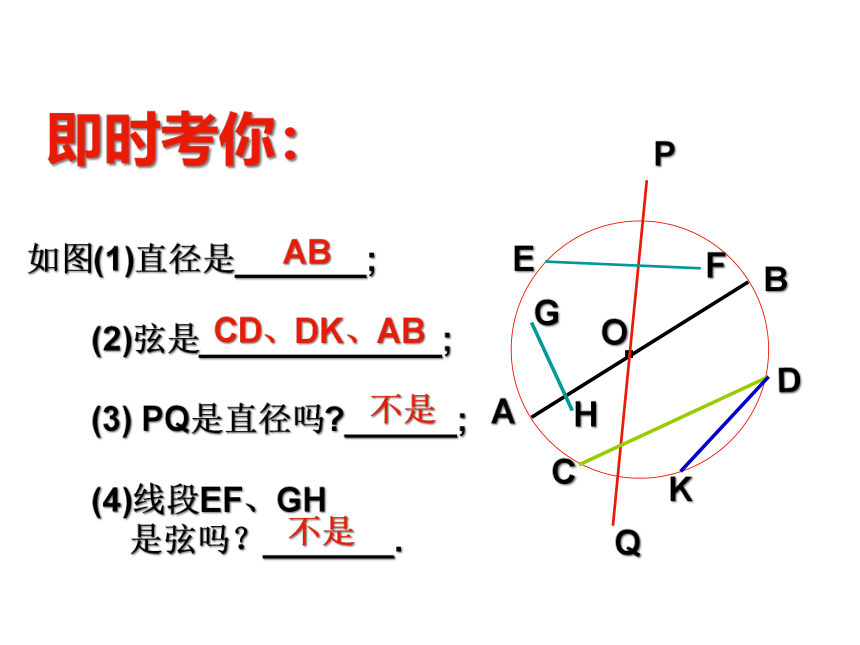
即时考你:
.
O
A
D
Q
C
B
P
H
G
F
E
如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗?______;
(4)线段EF、GH
是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
●
O
B
C
A
1.如图,半径有:______________
OA、OB、OC
③若∠AOB=60°,
则△AOB是_____三角形.
2.如图,弦有:______________
AB、BC、
AC
等边
① OA = OB= OC
② 在同一个圆中,所有的半径都相等。
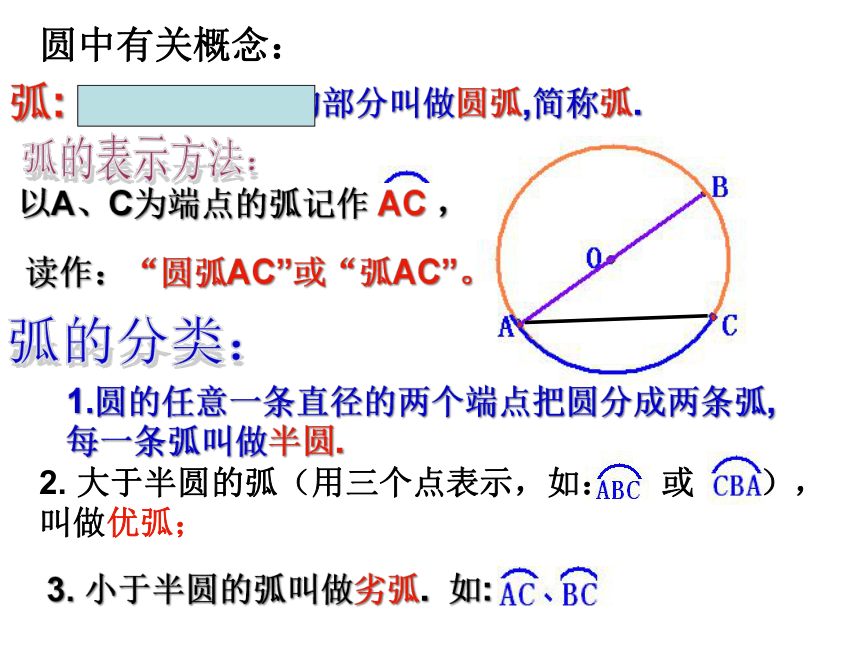
弧:
以A、C为端点的弧记作 AC ,
读作:“圆弧AC”或“弧AC”。
2. 大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;
3. 小于半圆的弧叫做劣弧. 如:
1.圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.
圆中有关概念:
圆上任意两点的部分叫做圆弧,简称弧.
●
O
B
C
A
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
⌒
AB
⌒
BC
劣弧有:
优弧有:
⌒
ACB
⌒
BAC
如图,请正确的方式表示出以点A为端点的优弧及劣弧.
⌒
ACD
⌒
⌒
⌒
ACF
ADE
ADC
AC
AE
AF
AD
⌒
⌒
⌒
⌒
等圆与等弧
能够重合的两个圆是等圆。
在同圆或等圆中,能够互相重合的弧叫做等弧。
容易看出:半径相等的两个圆是等圆。
反过来说,同圆或等圆的半径相等。
想一想
判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(7)圆心相同,半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
( )
( )
( )
( )
( )
( )
( )
( )
同步练习
3、判断
(1)半圆是弧,但弧不是半圆。( )
(2)过圆上任意一点只能作一条弦,且这条弦是直径。( )
(3)弦是直径,但直径不是弦。( )
(4)直径是圆中最长的弦。( )
(5)长度相等的两条弧是等弧。( )
同步练习
4、选择
(1)下列说法中,正确的是( )。
①线段是弦;②直径是弦;③经过圆心的弦是直径;④经过圆上一点有无数条直径。
A、①② B、②③
C、②④ D、③④
B
如图,矩形ABCD的对角线AC与BD相交于点O,
求证:点A、B、C、D在以点O为圆心的同一个圆上
基础训练
1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.平面上一点和⊙O上的最近点距离为4cm,最远点距离为
10cm,则这个圆的半径是______cm.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.
A
7或3
2
第5题
24°
5
A
C
如图,∠AOB=60°,试说明△ABO是等边三角形
如图,∠AOB=60°,试说明△ABO是等边三角形
已知,如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点,
求证:MC = NC。
如图,在圆O中,AB是直径,弦BC=4cm,AC 与AB成45度的角,求圆心到弦AC的距离
如图所示,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,求证:△OCD是等腰三角形.
如图所示,AB、CD是⊙O的两条互相垂直的直径.
(1)试判断四边形ACBD是什么特殊的四边形,为什么?
(2)若⊙O的半径r=2?cm,求四边形ADBC的周长.
如图,CD是⊙O的直径,点A在DC的延长线上,AE交⊙O于B、E,AB等于⊙O的半径,∠DOE=78°,求∠A的度数.
圆
.
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆
圆心
半径
记作:
读作:圆O
⊙
O
·
r
O
A
O
A
r
圆心和半径是构成圆的两个重要元素,
圆心确定圆的位置,半径确定圆的大小,
只有当给出圆心和半径这两个要素之后,
才能够确定一个圆。
小亮画一个半径为2cm的⊙O,
圆上各点与圆心的距离有什么特点?
车轮为什么做成圆形?
应 用 新 知
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
议一议
为什么车轮是圆的呢?椭圆或正方形可以吗
.
O
A
B
C
弦
连接圆上任意两点的线段。
直径
经过圆心的弦。
直径
注意:
凡直径都是弦,是圆中最长的弦
但弦不一定是直径.
圆中有关概念:
即时考你:
.
O
A
D
Q
C
B
P
H
G
F
E
如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗?______;
(4)线段EF、GH
是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
●
O
B
C
A
1.如图,半径有:______________
OA、OB、OC
③若∠AOB=60°,
则△AOB是_____三角形.
2.如图,弦有:______________
AB、BC、
AC
等边
① OA = OB= OC
② 在同一个圆中,所有的半径都相等。
弧:
以A、C为端点的弧记作 AC ,
读作:“圆弧AC”或“弧AC”。
2. 大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;
3. 小于半圆的弧叫做劣弧. 如:
1.圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.
圆中有关概念:
圆上任意两点的部分叫做圆弧,简称弧.
●
O
B
C
A
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
⌒
AB
⌒
BC
劣弧有:
优弧有:
⌒
ACB
⌒
BAC
如图,请正确的方式表示出以点A为端点的优弧及劣弧.
⌒
ACD
⌒
⌒
⌒
ACF
ADE
ADC
AC
AE
AF
AD
⌒
⌒
⌒
⌒
等圆与等弧
能够重合的两个圆是等圆。
在同圆或等圆中,能够互相重合的弧叫做等弧。
容易看出:半径相等的两个圆是等圆。
反过来说,同圆或等圆的半径相等。
想一想
判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(7)圆心相同,半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
( )
( )
( )
( )
( )
( )
( )
( )
同步练习
3、判断
(1)半圆是弧,但弧不是半圆。( )
(2)过圆上任意一点只能作一条弦,且这条弦是直径。( )
(3)弦是直径,但直径不是弦。( )
(4)直径是圆中最长的弦。( )
(5)长度相等的两条弧是等弧。( )
同步练习
4、选择
(1)下列说法中,正确的是( )。
①线段是弦;②直径是弦;③经过圆心的弦是直径;④经过圆上一点有无数条直径。
A、①② B、②③
C、②④ D、③④
B
如图,矩形ABCD的对角线AC与BD相交于点O,
求证:点A、B、C、D在以点O为圆心的同一个圆上
基础训练
1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.平面上一点和⊙O上的最近点距离为4cm,最远点距离为
10cm,则这个圆的半径是______cm.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.
A
7或3
2
第5题
24°
5
A
C
如图,∠AOB=60°,试说明△ABO是等边三角形
如图,∠AOB=60°,试说明△ABO是等边三角形
已知,如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点,
求证:MC = NC。
如图,在圆O中,AB是直径,弦BC=4cm,AC 与AB成45度的角,求圆心到弦AC的距离
如图所示,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,求证:△OCD是等腰三角形.
如图所示,AB、CD是⊙O的两条互相垂直的直径.
(1)试判断四边形ACBD是什么特殊的四边形,为什么?
(2)若⊙O的半径r=2?cm,求四边形ADBC的周长.
如图,CD是⊙O的直径,点A在DC的延长线上,AE交⊙O于B、E,AB等于⊙O的半径,∠DOE=78°,求∠A的度数.
同课章节目录
