人教版数学九年级下册27.2.2相似三角形的性质课件(19张PPT)
文档属性
| 名称 | 人教版数学九年级下册27.2.2相似三角形的性质课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:34:00 | ||
图片预览




文档简介
相似三角形
的性质
人教版2011新课标数学九年级下册
27.2.2
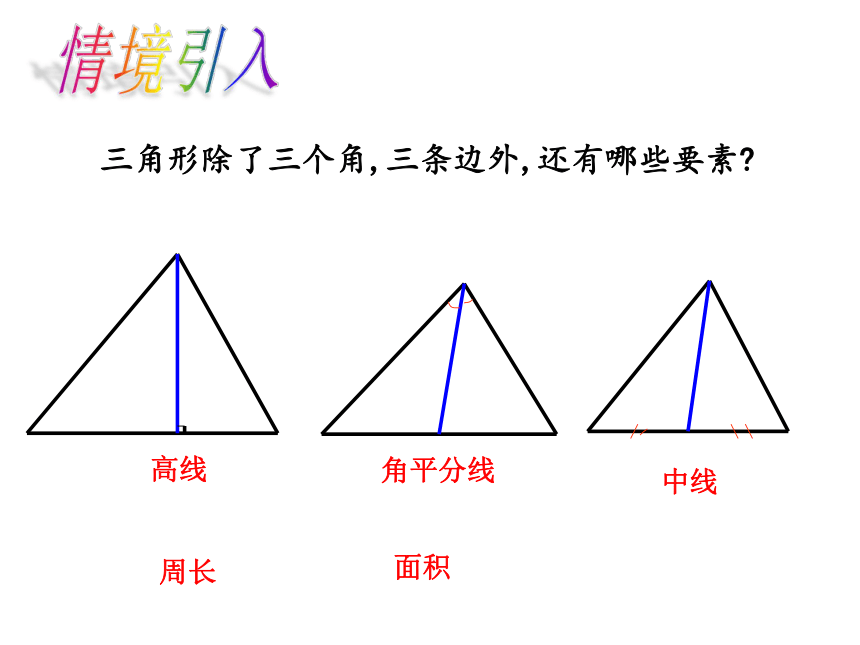
高线
角平分线
中线
情境引入
三角形除了三个角,三条边外,还有哪些要素?
周长
面积
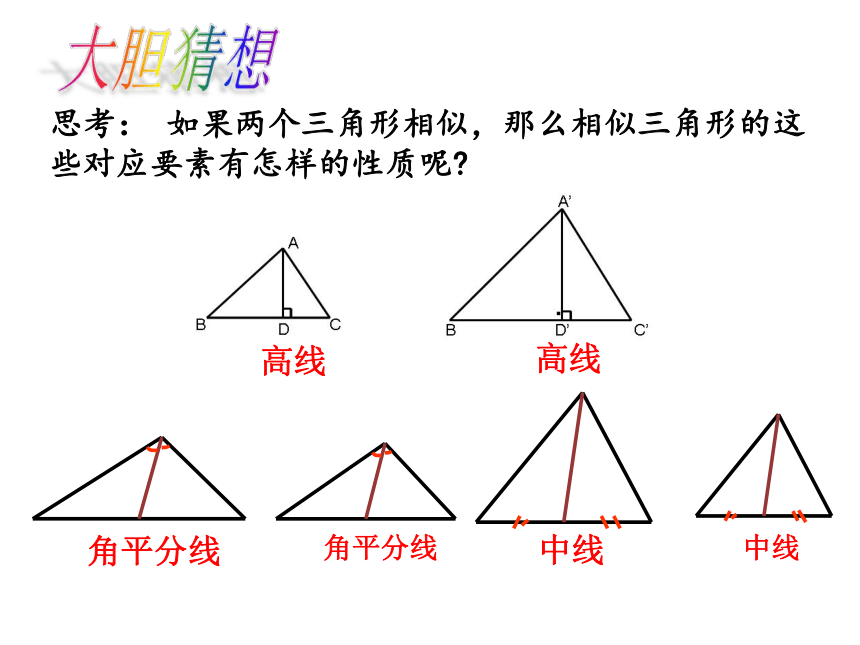
角平分线
角平分线
中线
中线
思考: 如果两个三角形相似,那么相似三角形的这些对应要素有怎样的性质呢?
高线
高线
大胆猜想
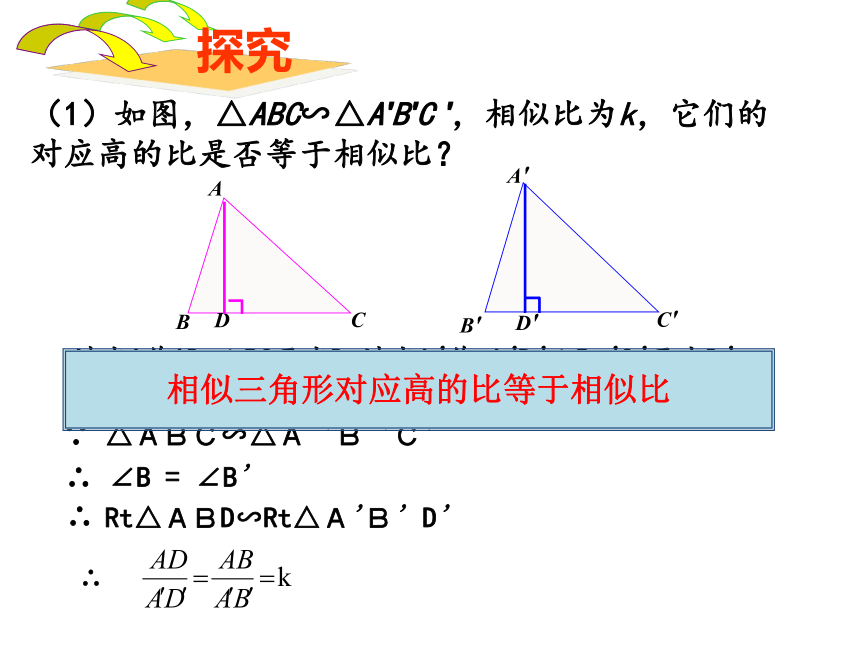
∵ △ABC∽△A 'B 'C'
∴ ∠B = ∠B'
Rt△ABD∽Rt△A'B' D'
∴
∴ ∠ADB = ∠A'D'B' =900
∴
(1)如图,△ABC∽△A'B'C ',相似比为k,它们的对应高的比是否等于相似比?
A
B
C
A'
B'
C'
D'
D
过点A作AD ⊥BC于点D,过点A'作 A'D'⊥B 'C'于点D'
相似三角形对应高的比等于相似比
探究
(2)如图,△ABC∽△A'B'C',相似比为k,它们的对应角平分线的比是否也等于相似比?
A
B
C
A'
B'
C'
D
D'
对应中线的比呢?
A
B
C
A'
B'
C'
D
D'
探究
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
通过以上的探究你有什么发现?
相似三角形对应线段的比等于相似比.
探究
A
B
C
A'
B'
C'
(3)如图,△ABC∽△A'B'C',相似比为k,它们的周长比是多少?
△ABC∽△A'B'C',相似比为k,
AB=k A'B',BC=kB'C',CA=kC'A'
∵
∴
∴
∴
即
相似三角形周长的比等于相似比
探究
(4)如图,△ABC∽△A'B'C',相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
D'
D
如图,分别作出△ABC和△A'B'C'的高AD和A'D'.
∵ △ABC∽△A'B'C'
这样,得到:
相似三角形面积的比等于相似比的平方.
∴BC=k B'C'
AD=k A'D'
探究
1(抢答)两个相似三角形对应边的比为3:5,那么相似比为 ,对应边上的高之比为 ,对应边上的中线比为 ,对应角的角平分线比为 ,周长比为 面积比为 .
2(抢答)两个相似三角形的面积比为1:4,那么周长比为 .
3:5
3:5
3:5
3:5
小试牛刀
3:5
9:25
1:2
相似三角形的相似比等于面积比的算术平方根.
3、把 一个三角形变成和它相似的三角形,则如果边长扩大为原来的5倍,那么面积扩大为 倍;
如果面积扩大为原来的100倍,那么边长扩大为原来的 倍。
25
10
4、已知△ABC∽△A′B′C′,AC: A′ C′=4:3。
(1)若△ABC的周长为24cm,则△A′B′C′的周长
为 cm;
(2)若△ABC的面积为32 cm2 ,则△A′B′C′的
面积为 cm2.
18
18
例.如图,在△ABC 和△DEF 中,AB=2DE,AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高是 6,面积为 ,求△DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
运用提高
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF,
∴ .
又 ∠A=∠D ,
∴△DEF∽△ABC ,△DEF 与△ABC 的相似比为
∵ △ABC的边BC上的高是 6,面积是 ,
∴ △DEF的边EF上的高为 ×6=3,
面积为( )× = .
2
本节课你有哪些收获?
小结与反思
对应角相等
对应边成比例
对应高
对应中线
对应角平分线
周长
面积比等于相似比的平方
相似三角形的性质
的比等于相似比
小结与反思
1、两个相似三角形对应边比为2:3,那么相似比为 ,周长比为 ,面积比为 。
2:3
4:9
2:3
当堂检测
2.在△ABC和 △DEF中,AB=2DE,AC=2DF, ∠A= ∠D.如果△ABC的周长是16,面积是12,那么△DEF的周长、面积分别为 ( )
A 8,3 B 8,6 C 4,3 D 4,6
3.已知两个相似三角形的周长的比为1:2,它们的面积和为25,则较大三角形的面积为 。
A
20
4. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化?
解:∵比例是6∶2 = 3∶1
∴这次复印的放缩比例是300%
又∵面积比是9∶1
∴这个多边形的面积扩大到9倍
5.如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为4:5,那么该怎么切割呢?
A
B
C
D
E
必做题:教科书第 39 页练习 第 1,2,3 题.
选做题:
如图,△ABC 的面积为 100,周长为 80,AB=20,点 D 是 AB 上一点,BD=12,过点 D 作 DE∥BC,交 AC于点 E.(1)求△ADE 的周长和面积;(2)过点 E 作 EF∥AB,EF 交 BC 于点 F,求△EFC 和四边形 DBFE 的面积.
分层作业 着眼发展
B
A
D
C
E
F
再见
的性质
人教版2011新课标数学九年级下册
27.2.2
高线
角平分线
中线
情境引入
三角形除了三个角,三条边外,还有哪些要素?
周长
面积
角平分线
角平分线
中线
中线
思考: 如果两个三角形相似,那么相似三角形的这些对应要素有怎样的性质呢?
高线
高线
大胆猜想
∵ △ABC∽△A 'B 'C'
∴ ∠B = ∠B'
Rt△ABD∽Rt△A'B' D'
∴
∴ ∠ADB = ∠A'D'B' =900
∴
(1)如图,△ABC∽△A'B'C ',相似比为k,它们的对应高的比是否等于相似比?
A
B
C
A'
B'
C'
D'
D
过点A作AD ⊥BC于点D,过点A'作 A'D'⊥B 'C'于点D'
相似三角形对应高的比等于相似比
探究
(2)如图,△ABC∽△A'B'C',相似比为k,它们的对应角平分线的比是否也等于相似比?
A
B
C
A'
B'
C'
D
D'
对应中线的比呢?
A
B
C
A'
B'
C'
D
D'
探究
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
通过以上的探究你有什么发现?
相似三角形对应线段的比等于相似比.
探究
A
B
C
A'
B'
C'
(3)如图,△ABC∽△A'B'C',相似比为k,它们的周长比是多少?
△ABC∽△A'B'C',相似比为k,
AB=k A'B',BC=kB'C',CA=kC'A'
∵
∴
∴
∴
即
相似三角形周长的比等于相似比
探究
(4)如图,△ABC∽△A'B'C',相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
D'
D
如图,分别作出△ABC和△A'B'C'的高AD和A'D'.
∵ △ABC∽△A'B'C'
这样,得到:
相似三角形面积的比等于相似比的平方.
∴BC=k B'C'
AD=k A'D'
探究
1(抢答)两个相似三角形对应边的比为3:5,那么相似比为 ,对应边上的高之比为 ,对应边上的中线比为 ,对应角的角平分线比为 ,周长比为 面积比为 .
2(抢答)两个相似三角形的面积比为1:4,那么周长比为 .
3:5
3:5
3:5
3:5
小试牛刀
3:5
9:25
1:2
相似三角形的相似比等于面积比的算术平方根.
3、把 一个三角形变成和它相似的三角形,则如果边长扩大为原来的5倍,那么面积扩大为 倍;
如果面积扩大为原来的100倍,那么边长扩大为原来的 倍。
25
10
4、已知△ABC∽△A′B′C′,AC: A′ C′=4:3。
(1)若△ABC的周长为24cm,则△A′B′C′的周长
为 cm;
(2)若△ABC的面积为32 cm2 ,则△A′B′C′的
面积为 cm2.
18
18
例.如图,在△ABC 和△DEF 中,AB=2DE,AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高是 6,面积为 ,求△DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
运用提高
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF,
∴ .
又 ∠A=∠D ,
∴△DEF∽△ABC ,△DEF 与△ABC 的相似比为
∵ △ABC的边BC上的高是 6,面积是 ,
∴ △DEF的边EF上的高为 ×6=3,
面积为( )× = .
2
本节课你有哪些收获?
小结与反思
对应角相等
对应边成比例
对应高
对应中线
对应角平分线
周长
面积比等于相似比的平方
相似三角形的性质
的比等于相似比
小结与反思
1、两个相似三角形对应边比为2:3,那么相似比为 ,周长比为 ,面积比为 。
2:3
4:9
2:3
当堂检测
2.在△ABC和 △DEF中,AB=2DE,AC=2DF, ∠A= ∠D.如果△ABC的周长是16,面积是12,那么△DEF的周长、面积分别为 ( )
A 8,3 B 8,6 C 4,3 D 4,6
3.已知两个相似三角形的周长的比为1:2,它们的面积和为25,则较大三角形的面积为 。
A
20
4. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化?
解:∵比例是6∶2 = 3∶1
∴这次复印的放缩比例是300%
又∵面积比是9∶1
∴这个多边形的面积扩大到9倍
5.如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为4:5,那么该怎么切割呢?
A
B
C
D
E
必做题:教科书第 39 页练习 第 1,2,3 题.
选做题:
如图,△ABC 的面积为 100,周长为 80,AB=20,点 D 是 AB 上一点,BD=12,过点 D 作 DE∥BC,交 AC于点 E.(1)求△ADE 的周长和面积;(2)过点 E 作 EF∥AB,EF 交 BC 于点 F,求△EFC 和四边形 DBFE 的面积.
分层作业 着眼发展
B
A
D
C
E
F
再见
