湘教版七年级数学下册课件:2.1.2 第2课时 积的乘方(15张PPT)
文档属性
| 名称 | 湘教版七年级数学下册课件:2.1.2 第2课时 积的乘方(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:55:59 | ||
图片预览






文档简介
第2章 整式的乘法
2.1.2 第2课时 积的乘方
知识回顾
同底数幂相乘,底数不变,指数相加.
即:am · an = am+n (m,n都是正整数).
(am)n =amn
幂的乘方,底数不变,指数相乘.
情景引入
(ab)3=
ab·ab·ab
(2) 为了计算(化简)ab·ab·ab,可以应用乘法的交换律和结合律.
又可以把它写成什么形式?
=a·a·a · b·b·b
=a3·b3
(3)由特殊的 (ab)3=a3b3 出发,你能想到一般的公式吗?
猜想
(ab)n=
anbn
(1) 根据乘方的定义(幂的意义),(ab)3表示什么?
情景引入
(4)在(ab)3运算过程中你用到了哪些知识?
(ab)3 =(ab)·(ab)·(ab)
=(a·a·a)(b·b·b)
= a3b3.
3个ab
3个a
3个b
(幂的意义)
(乘法交换律和结合律)
(幂的意义)
情景引入
(5)怎样计算(2b)3?在运算过程中你用到了哪些知识?
(2b)3 =(2b)·(2b)·(2b) (幂的意义)
=(2·2·2)(b·b·b) (乘法交换律和结合律)
= 23b3. (幂的意义)
3个2b
3个2
3个b
= 8b3. (乘方的运算)
情景引入
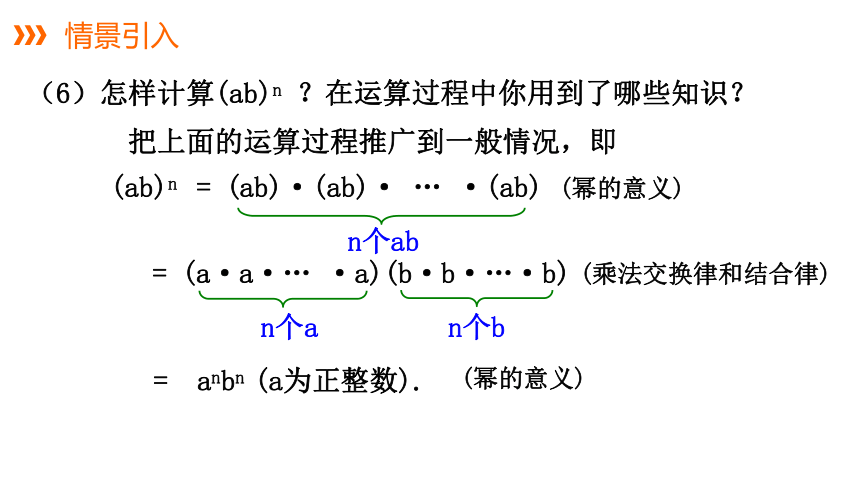
把上面的运算过程推广到一般情况,即
(ab)n = (ab)·(ab)· … ·(ab)
n个ab
= (a·a·… ·a)(b·b·…·b)
n个a
n个b
= anbn (a为正整数).
(6)怎样计算(ab)n ?在运算过程中你用到了哪些知识?
(幂的意义)
(乘法交换律和结合律)
(幂的意义)
获取新知
积的乘方
乘方的积
(ab)n =
an·bn
(m,n都是正整数)
积的乘方法则
用自己的语言叙述一下积的乘方法则 ?
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
你能说出法则中“因式”这两个字的意义吗?
情景引入
(abc)n=an · bn · cn
怎样证明 ?
(7)三个或三个以上的积的乘方,是否也具有上面的性质?
(8)怎样用公式表示?
(abc)n = (abc)· … ·(abc)
n个abc
=(a · a… ·a)·(b · b … ·b) ·(c · c … ·c)
n个a
n个b
n个c
= anbncn
有
例题讲解
例1 计算:
(1)(-2x)3; (2)(-4xy)2;
(3)(xy2)3; (4)
例题讲解
(1) (-2x)3
(2) (-4xy)2
解 (-2x)3
= (-2)3 ·x3
= -8x3.
解 (-4xy)2
= (-4)2·x2·y2
= 16x2y2.
(3) (xy2)3
解 (xy2)3
= x3 ·(y2)3
= x3y6.
例题讲解
例2 计算:
2(a2b2)3 - 3(a3b3)2.
解 2(a2b2)3 -3(a3b3)2
= 2a6b6 -3a6b6
= -a6b6.
例题讲解
【归纳总结】幂的混合运算的顺序:
先算乘方,再算乘除,最后算加减.
情景引入
随堂演练
D
B
B
随堂演练
-8
2.1.2 第2课时 积的乘方
知识回顾
同底数幂相乘,底数不变,指数相加.
即:am · an = am+n (m,n都是正整数).
(am)n =amn
幂的乘方,底数不变,指数相乘.
情景引入
(ab)3=
ab·ab·ab
(2) 为了计算(化简)ab·ab·ab,可以应用乘法的交换律和结合律.
又可以把它写成什么形式?
=a·a·a · b·b·b
=a3·b3
(3)由特殊的 (ab)3=a3b3 出发,你能想到一般的公式吗?
猜想
(ab)n=
anbn
(1) 根据乘方的定义(幂的意义),(ab)3表示什么?
情景引入
(4)在(ab)3运算过程中你用到了哪些知识?
(ab)3 =(ab)·(ab)·(ab)
=(a·a·a)(b·b·b)
= a3b3.
3个ab
3个a
3个b
(幂的意义)
(乘法交换律和结合律)
(幂的意义)
情景引入
(5)怎样计算(2b)3?在运算过程中你用到了哪些知识?
(2b)3 =(2b)·(2b)·(2b) (幂的意义)
=(2·2·2)(b·b·b) (乘法交换律和结合律)
= 23b3. (幂的意义)
3个2b
3个2
3个b
= 8b3. (乘方的运算)
情景引入
把上面的运算过程推广到一般情况,即
(ab)n = (ab)·(ab)· … ·(ab)
n个ab
= (a·a·… ·a)(b·b·…·b)
n个a
n个b
= anbn (a为正整数).
(6)怎样计算(ab)n ?在运算过程中你用到了哪些知识?
(幂的意义)
(乘法交换律和结合律)
(幂的意义)
获取新知
积的乘方
乘方的积
(ab)n =
an·bn
(m,n都是正整数)
积的乘方法则
用自己的语言叙述一下积的乘方法则 ?
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
你能说出法则中“因式”这两个字的意义吗?
情景引入
(abc)n=an · bn · cn
怎样证明 ?
(7)三个或三个以上的积的乘方,是否也具有上面的性质?
(8)怎样用公式表示?
(abc)n = (abc)· … ·(abc)
n个abc
=(a · a… ·a)·(b · b … ·b) ·(c · c … ·c)
n个a
n个b
n个c
= anbncn
有
例题讲解
例1 计算:
(1)(-2x)3; (2)(-4xy)2;
(3)(xy2)3; (4)
例题讲解
(1) (-2x)3
(2) (-4xy)2
解 (-2x)3
= (-2)3 ·x3
= -8x3.
解 (-4xy)2
= (-4)2·x2·y2
= 16x2y2.
(3) (xy2)3
解 (xy2)3
= x3 ·(y2)3
= x3y6.
例题讲解
例2 计算:
2(a2b2)3 - 3(a3b3)2.
解 2(a2b2)3 -3(a3b3)2
= 2a6b6 -3a6b6
= -a6b6.
例题讲解
【归纳总结】幂的混合运算的顺序:
先算乘方,再算乘除,最后算加减.
情景引入
随堂演练
D
B
B
随堂演练
-8
