初中数学人教版七年级上册第四章4.2直线、射线、线段练习题(Word版 含解析)
文档属性
| 名称 | 初中数学人教版七年级上册第四章4.2直线、射线、线段练习题(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 122.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览





文档简介
初中数学人教版七年级上册第四章4.2直线、射线、线段练习题
一、选择题
下列说法中正确的是
A.
延长射线OA到点B
B.
线段AB为直线AB的一部分
C.
射线OM与射线MO表示同一条射线
D.
一条直线由两条射线组成
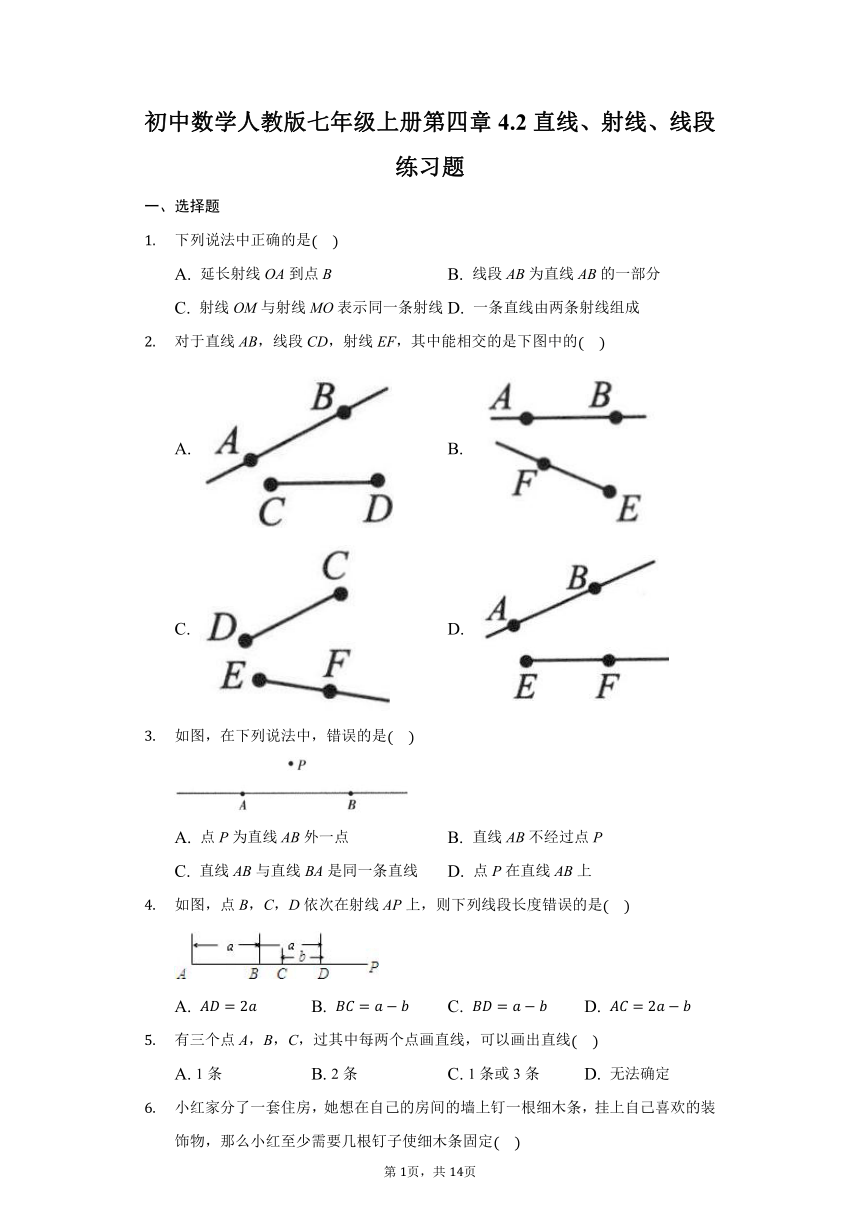
对于直线AB,线段CD,射线EF,其中能相交的是下图中的
A.
B.
C.
D.
如图,在下列说法中,错误的是
A.
点P为直线AB外一点
B.
直线AB不经过点P
C.
直线AB与直线BA是同一条直线
D.
点P在直线AB上
如图,点B,C,D依次在射线AP上,则下列线段长度错误的是
A.
B.
C.
D.
有三个点A,B,C,过其中每两个点画直线,可以画出直线
A.
1条
B.
2条
C.
1条或3条
D.
无法确定
小红家分了一套住房,她想在自己的房间的墙上钉一根细木条,挂上自己喜欢的装饰物,那么小红至少需要几根钉子使细木条固定
A.
1根
B.
2根
C.
3根
D.
4根
如图,,,则CD等于?
?
A.
1cm
B.
2cm
C.
3cm
D.
4cm
A,B,C三点在同一条直线上,如果线段,,那么A,C两点的距离为
A.
8cm
B.
2cm
C.
2cm或8cm
D.
以上均不正确
把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释正确的是
A.
线段可以比较大小
B.
线段有两个端点
C.
两点之间线段最短
D.
过两点有且只有一条直线
点A,B,C在同一条数轴上,其中点A,B表示的数分别为、1,若,则AC等于
A.
3
B.
2
C.
3或5
D.
2或6
如图,点A,B,C是直线l上的三个点,图中共有线段条数是
A.
1条
B.
2条
C.
3条
D.
4条
如图所示,C是线段AB的中点,D在线段CB上,,,则
A.
20
B.
12
C.
10
D.
8
二、填空题
如图,A,B,C是直线l上的三个点,图中共有??????????条线段.
把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理是______.
如图所示,OA,OB是两条射线,C是OA上一点,D,E是OB上两点,则图中共有____条线段,它们分别是_____________________;图中共有_____条射线,它们分别是__________________.
已知A,B,C三点在同一条直线上,,,M,N分别是AB,BC的中点,则线段MN的长是________.
三、解答题
如图,已知点C在线段AB上,线段,,M,N分别是AC,BC的中点,求线段MN的长
如图,已知点C在线段AB上,线段,M,N分别是AC,BC的中点,求线段MN的长
如图,已知点C在线段AB上,线段,M,N分别是AC,BC的中点,求线段MN的长
如图,已知点C在线段AB的延长线上,线段,M,N分别是AC,BC的中点,求线段MN的长.
已知平面上有一条线段,探讨下列问题:
平面上是否存在一点C,使它到A,B两点的距离之和等于说明理由
平面上是否存在一点D,使它到A,B两点的距离之和等于若存在,它的位置唯一吗
当点E到A,B两点的距离之和等于20cm时,点E一定在直线AB外吗请举例说明.
如图,已知C是线段AB的中点,点D在线段CB上,且厘米,厘米.
求线段CD的长度;
若将题中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
A,B两点在数轴上的位置如图所示,其中点A表示的有理数为,且点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为秒.
当时,AP的长为??????????,点P表示的有理数为??????????.
当时,求t的值.
为线段AP的中点,N为线段PB的中点在点P运动的过程中,线段MN的长度是否发生变化若发生变化,请说明理由若不发生变化,请你画出图形,并求出线段MN的长.
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查的是直线,射线,线段的有关知识,利用直线、射线、线段的特征判定即可.
【解答】
解:延长射线OA到点B,射线OA是无限延伸的,故选项错误;
B.线段AB为直线AB的一部分是正确的;
C.射线OM与射线MO表示两条射线,故选项错误;
D.一条直线不一定由两条射线组成,故选项错误.
故选B.
2.【答案】B
【解析】
【分析】
本题考查了直线、射线、线段,熟记定义并准确识图是解题的关键根据直线、射线、线段的定义对各选项分析判断利用排除法求解.
【解答】
解:A、直线AB与线段CD不能相交,故本选项错误;
B、直线AB与射线EF能够相交,故本选项正确;
C、射线EF与线段CD不能相交,故本选项错误;
D、直线AB与射线EF不能相交,故本选项错误.
故选B.
3.【答案】D
【解析】
【分析】
考查直线、射线和线段的意义.注意图形结合的解题思想结合图形,对选项一一分析,选出正确答案.
【解答】
解:A、点P为直线AB外一点,符合图形描述,选项正确;
B、直线AB不经过点P,符合图形描述,选项正确;
C、直线AB与直线BA是同一条直线,符合图形描述,选项正确;
D、点P在直线AB上应改为点P在直线AB外一点,选项错误.
故选D.
4.【答案】C
【解析】
【分析】
本题主要考查的是两点间的距离的有关知识,直接根据数轴结合两点间的距离公式对给出的各个选项进行逐一分析即可.
【解答】
解:,,故本选项正确;
B.,,,故本选项正确;
C.由图示可知,,故本选项错误;
D.,,,故本选项正确.
故选C.
5.【答案】C
【解析】
【分析】
此题考查直线的基本性质:两点确定一条直线,分当三点在同一条直线上时,当三点不在同一条直线上时讨论求解即可.
【解答】
解:当三点在同一条直线上时,只能画一条;
当三点不在同一条直线上时可以画3条;
故选C.
6.【答案】B
【解析】
【分析】
本题考查直线的性质.经过两点有一条直线,并且只有一条直线,即两点确定一条直线.根据直线的性质求解,判定正确选项.
【解答】
解:根据直线的性质,小红至少需要2根钉子使细木条固定.只有B符合.
故选B.
7.【答案】B
【解析】
【分析】
本题考查了线段的和差关系,解题的关键是求出BD的长度先根据已知条件,利用求出线段BD的长度,再利用求出线段CD长度即可.
【解答】
解:,,
,
,
.
故选B.
8.【答案】C
【解析】
【分析】
本题考查了两点间的距离,属于基础题,关键是分类讨论A,B,C三点是否在一条直线上时分两种情况:C在AB之间,有;C不在AB之间,有,分别得出A,C两点间的距离.
【解答】
解:C在AB之间,有;
C不在AB之间,有.
故A,C两点间的距离是2cm或8cm.
故选C.
9.【答案】C
【解析】解:把一条弯曲的公路改成直道,可以缩短路程,其道理是两点之间线段最短,
故选:C.
根据线段的性质:两点之间线段最短进行解答即可.
此题主要考查了线段的性质,关键是掌握两点之间线段最短.
10.【答案】D
【解析】
【分析】
本题主要考查的是数轴,两点间的距离,运用了分类讨论思想,分情况讨论A,B,C三点的位置关系,即点C在线段AB内,点C在线段AB外进行求解即可.
【解答】
解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.
点A、B表示的数分别为、1,
线段AB的长度,
第一种情况:在线段AB外,
;
第二种情况:在线段AB内,
.
故选D.
11.【答案】C
【解析】
【分析】
本题主要考查了线段的定义,记住线段是直线上两点及其之间的部分是解题的关键.
写出所有的线段,然后再计算条数.
【解答】
解:图中线段有:线段AB、线段AC、线段BC,共3条.
故选:C.
12.【答案】D
【解析】
【分析】
此题考查的知识点是线段的和差,由已知得,又由C是线段AB的中点可求出,从而求得.
【解答】
解:,
是线段AB的中点,
,
.
故选D.
13.【答案】3
【解析】
【分析】
本题考查了线段,记住线段是直线上两点及其之间的部分是解题的关键,写出所有的线段,然后再计算条数
【解答】
解:图中线段有:线段AB、线段AC、线段BC,共三条.
故答案为3.
14.【答案】两点之间线段最短
【解析】解:把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理是两点之间线段最短,
故答案为:两点之间线段最短.
根据线段的性质,可得答案.
本题考查了线段的性质,熟记线段的性质是解题关键.
15.【答案】6条;OC,OD,OE,CD,CE,DE;5条;CA,OC,OD,DE,EB
【解析】
【分析】
本题考查了射线、线段的概念,根据射线、线段的概念,结合图形,即可求得答案.
【解答】
解:图中共有6条线段,它们分别是OC,OD,OE,CD,CE,DE;
图中共有5条射线,它们分别是CA,OC,OD,DE,EB。
故答案为6条;OC,OD,OE,CD,CE,DE;5条;CA,OC,OD,DE,EB.
16.【答案】7或1
【解析】
【分析】
本题考查了两点间的距离,利用线段的和差是解题关键,要分类讨论,以防遗漏.根据线段中点的性质,可得MB,NB,根据线段的和差,可得答案.
【解答】
解:由,,M、N分别为AB、BC中点,得
,.
在线段AB的延长线上,;
在线段AB上,;
在线段AB的反延长线上,,不成立,
综上所述:线段MN的长7或1.
故答案为7或1.
17.【答案】解因为M是AC的中点,N是BC的中点,
,.
.
是AC的中点,N是BC的中点,
,.
.
因为M是AC的中点,N是BC的中点,
,.
.
是AC的中点,N是BC的中点,
,.
.
【解析】本题考查的是线段的和差和线段的中点定义,熟知各线段之间的和、差及倍数关系是解答此题的关键.
此题的关键是先求出CN,CM的值才能进而求出MN的值;
根据的计算结果代入即可;
根据的计算结果代入即可;
求出MC,NC,代入即可.
18.【答案】解:不存在点C,使它到A,B两点的距离之和等于8厘米.因为两点之间线段最短;
存在点C,使它到A,B两点的距离之和等于10厘米,此时点C在线段AB上,它的位置不唯一;
不一定如图所示,当点E在线段BA的延长线上且时,点E不在直线AB外.
【解析】本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离,解题关键是知道反例的作用.
根据两点之间线段最短进行判断;
点C在线段AB上时,点C到A,B两点的距离之和等于10cm;
举反例,当点E在线段BA的延长线上时,不满足条件.
19.【答案】解:因为厘米,厘米,所以厘米.
因为C是AB的中点,所以厘米所以厘米;
如图,因为厘米,厘米,
所以厘米因为C是AB的中点,
所以厘米所以厘米.
【解析】本题主要考查的是两点间的距离的有关知识.
根据已知条件和图形即可计算CD的长度;
画出相应的示意图,即可求出此时线段CD的长度.
20.【答案】解:,;
当点P在点B左侧时,
,,
,
由题意得:,
解得:;
当点P在点B右侧时,由题意可得,
解得:;
综上,或6;
如图1,当点P在线段AB上时,
;
如图2,当点P在AB延长线上时,
;
综上所述,线段MN的长度不发生变化,其值为5.
【解析】
【分析】
本题考查了一元一次方程的应用和数轴,解题关键是根据题目给出的条件,找出合适的等量关系列出方程,再求解.根据题意知,点P表示的有理数为,将代入即可求得;
由、知,根据得出关于t的方程,解之即可得;
分类讨论:当点P在点A、B两点之间运动时,当点P运动到点B的左侧时,利用中点的定义和线段的和差易求出MN.
【解答】
解:设运动时间为t秒,
则,点P表示的有理数为,
当时,,点P表示的有理数为,
故答案为:2,;
见答案;
见答案.
第2页,共2页
第1页,共1页
一、选择题
下列说法中正确的是
A.
延长射线OA到点B
B.
线段AB为直线AB的一部分
C.
射线OM与射线MO表示同一条射线
D.
一条直线由两条射线组成
对于直线AB,线段CD,射线EF,其中能相交的是下图中的
A.
B.
C.
D.
如图,在下列说法中,错误的是
A.
点P为直线AB外一点
B.
直线AB不经过点P
C.
直线AB与直线BA是同一条直线
D.
点P在直线AB上
如图,点B,C,D依次在射线AP上,则下列线段长度错误的是
A.
B.
C.
D.
有三个点A,B,C,过其中每两个点画直线,可以画出直线
A.
1条
B.
2条
C.
1条或3条
D.
无法确定
小红家分了一套住房,她想在自己的房间的墙上钉一根细木条,挂上自己喜欢的装饰物,那么小红至少需要几根钉子使细木条固定
A.
1根
B.
2根
C.
3根
D.
4根
如图,,,则CD等于?
?
A.
1cm
B.
2cm
C.
3cm
D.
4cm
A,B,C三点在同一条直线上,如果线段,,那么A,C两点的距离为
A.
8cm
B.
2cm
C.
2cm或8cm
D.
以上均不正确
把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释正确的是
A.
线段可以比较大小
B.
线段有两个端点
C.
两点之间线段最短
D.
过两点有且只有一条直线
点A,B,C在同一条数轴上,其中点A,B表示的数分别为、1,若,则AC等于
A.
3
B.
2
C.
3或5
D.
2或6
如图,点A,B,C是直线l上的三个点,图中共有线段条数是
A.
1条
B.
2条
C.
3条
D.
4条
如图所示,C是线段AB的中点,D在线段CB上,,,则
A.
20
B.
12
C.
10
D.
8
二、填空题
如图,A,B,C是直线l上的三个点,图中共有??????????条线段.
把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理是______.
如图所示,OA,OB是两条射线,C是OA上一点,D,E是OB上两点,则图中共有____条线段,它们分别是_____________________;图中共有_____条射线,它们分别是__________________.
已知A,B,C三点在同一条直线上,,,M,N分别是AB,BC的中点,则线段MN的长是________.
三、解答题
如图,已知点C在线段AB上,线段,,M,N分别是AC,BC的中点,求线段MN的长
如图,已知点C在线段AB上,线段,M,N分别是AC,BC的中点,求线段MN的长
如图,已知点C在线段AB上,线段,M,N分别是AC,BC的中点,求线段MN的长
如图,已知点C在线段AB的延长线上,线段,M,N分别是AC,BC的中点,求线段MN的长.
已知平面上有一条线段,探讨下列问题:
平面上是否存在一点C,使它到A,B两点的距离之和等于说明理由
平面上是否存在一点D,使它到A,B两点的距离之和等于若存在,它的位置唯一吗
当点E到A,B两点的距离之和等于20cm时,点E一定在直线AB外吗请举例说明.
如图,已知C是线段AB的中点,点D在线段CB上,且厘米,厘米.
求线段CD的长度;
若将题中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
A,B两点在数轴上的位置如图所示,其中点A表示的有理数为,且点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为秒.
当时,AP的长为??????????,点P表示的有理数为??????????.
当时,求t的值.
为线段AP的中点,N为线段PB的中点在点P运动的过程中,线段MN的长度是否发生变化若发生变化,请说明理由若不发生变化,请你画出图形,并求出线段MN的长.
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查的是直线,射线,线段的有关知识,利用直线、射线、线段的特征判定即可.
【解答】
解:延长射线OA到点B,射线OA是无限延伸的,故选项错误;
B.线段AB为直线AB的一部分是正确的;
C.射线OM与射线MO表示两条射线,故选项错误;
D.一条直线不一定由两条射线组成,故选项错误.
故选B.
2.【答案】B
【解析】
【分析】
本题考查了直线、射线、线段,熟记定义并准确识图是解题的关键根据直线、射线、线段的定义对各选项分析判断利用排除法求解.
【解答】
解:A、直线AB与线段CD不能相交,故本选项错误;
B、直线AB与射线EF能够相交,故本选项正确;
C、射线EF与线段CD不能相交,故本选项错误;
D、直线AB与射线EF不能相交,故本选项错误.
故选B.
3.【答案】D
【解析】
【分析】
考查直线、射线和线段的意义.注意图形结合的解题思想结合图形,对选项一一分析,选出正确答案.
【解答】
解:A、点P为直线AB外一点,符合图形描述,选项正确;
B、直线AB不经过点P,符合图形描述,选项正确;
C、直线AB与直线BA是同一条直线,符合图形描述,选项正确;
D、点P在直线AB上应改为点P在直线AB外一点,选项错误.
故选D.
4.【答案】C
【解析】
【分析】
本题主要考查的是两点间的距离的有关知识,直接根据数轴结合两点间的距离公式对给出的各个选项进行逐一分析即可.
【解答】
解:,,故本选项正确;
B.,,,故本选项正确;
C.由图示可知,,故本选项错误;
D.,,,故本选项正确.
故选C.
5.【答案】C
【解析】
【分析】
此题考查直线的基本性质:两点确定一条直线,分当三点在同一条直线上时,当三点不在同一条直线上时讨论求解即可.
【解答】
解:当三点在同一条直线上时,只能画一条;
当三点不在同一条直线上时可以画3条;
故选C.
6.【答案】B
【解析】
【分析】
本题考查直线的性质.经过两点有一条直线,并且只有一条直线,即两点确定一条直线.根据直线的性质求解,判定正确选项.
【解答】
解:根据直线的性质,小红至少需要2根钉子使细木条固定.只有B符合.
故选B.
7.【答案】B
【解析】
【分析】
本题考查了线段的和差关系,解题的关键是求出BD的长度先根据已知条件,利用求出线段BD的长度,再利用求出线段CD长度即可.
【解答】
解:,,
,
,
.
故选B.
8.【答案】C
【解析】
【分析】
本题考查了两点间的距离,属于基础题,关键是分类讨论A,B,C三点是否在一条直线上时分两种情况:C在AB之间,有;C不在AB之间,有,分别得出A,C两点间的距离.
【解答】
解:C在AB之间,有;
C不在AB之间,有.
故A,C两点间的距离是2cm或8cm.
故选C.
9.【答案】C
【解析】解:把一条弯曲的公路改成直道,可以缩短路程,其道理是两点之间线段最短,
故选:C.
根据线段的性质:两点之间线段最短进行解答即可.
此题主要考查了线段的性质,关键是掌握两点之间线段最短.
10.【答案】D
【解析】
【分析】
本题主要考查的是数轴,两点间的距离,运用了分类讨论思想,分情况讨论A,B,C三点的位置关系,即点C在线段AB内,点C在线段AB外进行求解即可.
【解答】
解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.
点A、B表示的数分别为、1,
线段AB的长度,
第一种情况:在线段AB外,
;
第二种情况:在线段AB内,
.
故选D.
11.【答案】C
【解析】
【分析】
本题主要考查了线段的定义,记住线段是直线上两点及其之间的部分是解题的关键.
写出所有的线段,然后再计算条数.
【解答】
解:图中线段有:线段AB、线段AC、线段BC,共3条.
故选:C.
12.【答案】D
【解析】
【分析】
此题考查的知识点是线段的和差,由已知得,又由C是线段AB的中点可求出,从而求得.
【解答】
解:,
是线段AB的中点,
,
.
故选D.
13.【答案】3
【解析】
【分析】
本题考查了线段,记住线段是直线上两点及其之间的部分是解题的关键,写出所有的线段,然后再计算条数
【解答】
解:图中线段有:线段AB、线段AC、线段BC,共三条.
故答案为3.
14.【答案】两点之间线段最短
【解析】解:把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理是两点之间线段最短,
故答案为:两点之间线段最短.
根据线段的性质,可得答案.
本题考查了线段的性质,熟记线段的性质是解题关键.
15.【答案】6条;OC,OD,OE,CD,CE,DE;5条;CA,OC,OD,DE,EB
【解析】
【分析】
本题考查了射线、线段的概念,根据射线、线段的概念,结合图形,即可求得答案.
【解答】
解:图中共有6条线段,它们分别是OC,OD,OE,CD,CE,DE;
图中共有5条射线,它们分别是CA,OC,OD,DE,EB。
故答案为6条;OC,OD,OE,CD,CE,DE;5条;CA,OC,OD,DE,EB.
16.【答案】7或1
【解析】
【分析】
本题考查了两点间的距离,利用线段的和差是解题关键,要分类讨论,以防遗漏.根据线段中点的性质,可得MB,NB,根据线段的和差,可得答案.
【解答】
解:由,,M、N分别为AB、BC中点,得
,.
在线段AB的延长线上,;
在线段AB上,;
在线段AB的反延长线上,,不成立,
综上所述:线段MN的长7或1.
故答案为7或1.
17.【答案】解因为M是AC的中点,N是BC的中点,
,.
.
是AC的中点,N是BC的中点,
,.
.
因为M是AC的中点,N是BC的中点,
,.
.
是AC的中点,N是BC的中点,
,.
.
【解析】本题考查的是线段的和差和线段的中点定义,熟知各线段之间的和、差及倍数关系是解答此题的关键.
此题的关键是先求出CN,CM的值才能进而求出MN的值;
根据的计算结果代入即可;
根据的计算结果代入即可;
求出MC,NC,代入即可.
18.【答案】解:不存在点C,使它到A,B两点的距离之和等于8厘米.因为两点之间线段最短;
存在点C,使它到A,B两点的距离之和等于10厘米,此时点C在线段AB上,它的位置不唯一;
不一定如图所示,当点E在线段BA的延长线上且时,点E不在直线AB外.
【解析】本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离,解题关键是知道反例的作用.
根据两点之间线段最短进行判断;
点C在线段AB上时,点C到A,B两点的距离之和等于10cm;
举反例,当点E在线段BA的延长线上时,不满足条件.
19.【答案】解:因为厘米,厘米,所以厘米.
因为C是AB的中点,所以厘米所以厘米;
如图,因为厘米,厘米,
所以厘米因为C是AB的中点,
所以厘米所以厘米.
【解析】本题主要考查的是两点间的距离的有关知识.
根据已知条件和图形即可计算CD的长度;
画出相应的示意图,即可求出此时线段CD的长度.
20.【答案】解:,;
当点P在点B左侧时,
,,
,
由题意得:,
解得:;
当点P在点B右侧时,由题意可得,
解得:;
综上,或6;
如图1,当点P在线段AB上时,
;
如图2,当点P在AB延长线上时,
;
综上所述,线段MN的长度不发生变化,其值为5.
【解析】
【分析】
本题考查了一元一次方程的应用和数轴,解题关键是根据题目给出的条件,找出合适的等量关系列出方程,再求解.根据题意知,点P表示的有理数为,将代入即可求得;
由、知,根据得出关于t的方程,解之即可得;
分类讨论:当点P在点A、B两点之间运动时,当点P运动到点B的左侧时,利用中点的定义和线段的和差易求出MN.
【解答】
解:设运动时间为t秒,
则,点P表示的有理数为,
当时,,点P表示的有理数为,
故答案为:2,;
见答案;
见答案.
第2页,共2页
第1页,共1页
