湘教版七年级数学下册课件:4.4 第1课时 平行线的判定方法1(共16张ppt)
文档属性
| 名称 | 湘教版七年级数学下册课件:4.4 第1课时 平行线的判定方法1(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览




文档简介
第4章 平行线的性质
4.4 第1课时 平行线的判定方法1
情景引入
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
情景引入
(1)平面内两条直线的位置关系有几种?
(2)怎样过已知直线外一点画已知直线的平行线?
相交与平行
思考
获取新知
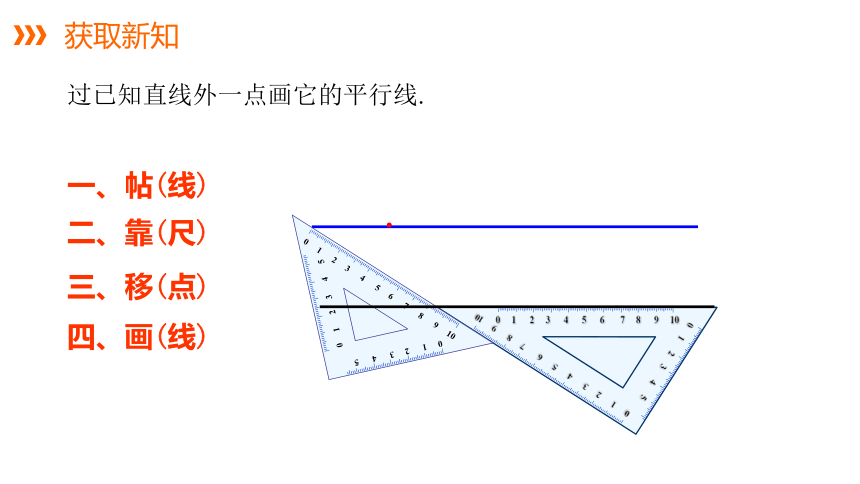
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
获取新知
1
a
b
.
P
2
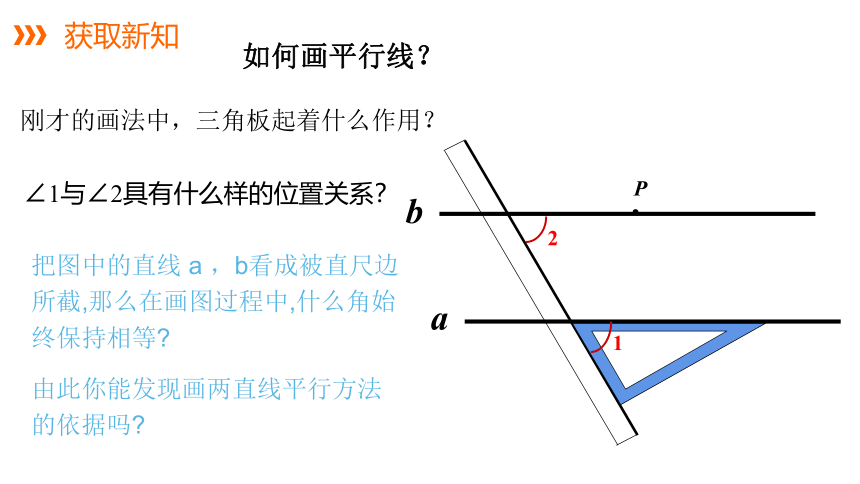
如何画平行线?
∠1与∠2具有什么样的位置关系?
把图中的直线 a ,b看成被直尺边所截,那么在画图过程中,什么角始终保持相等?
由此你能发现画两直线平行方法的依据吗?
刚才的画法中,三角板起着什么作用?
1
获取新知
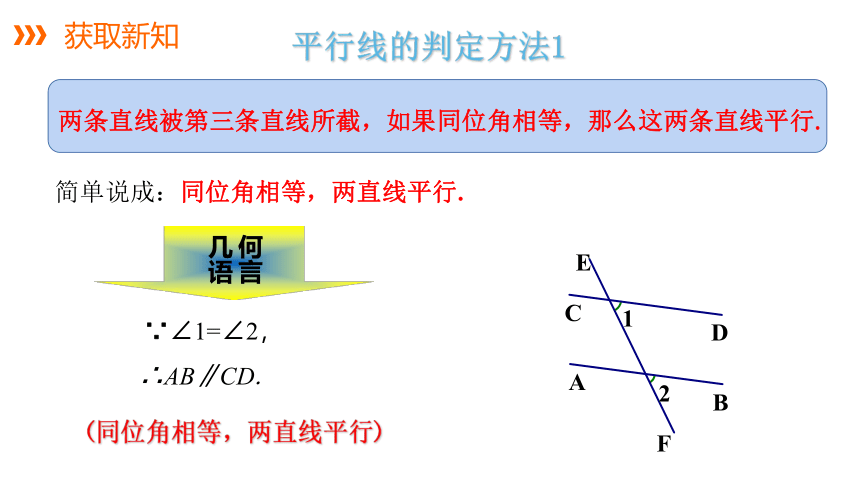
平行线的判定方法1
简单说成:同位角相等,两直线平行.
何言
几语
(同位角相等,两直线平行)
∵∠1=∠2,
∴AB∥CD.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
例题讲解
解 因为∠1+∠2 =180°,
例1 如图,直线AB,CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗? 为什么?
所以AB∥CD(同位角相等,两直线平行).
所以∠2=∠3.
而∠3 是∠1的补角,
即∠1+∠3=180°,
例题讲解
解 因为∠1=∠2(已知),
例2 如图,直线a, b被直线c,d所截,∠1=∠2,说明为什么∠4=∠5.
∠2=∠3 (对顶角相等),
所以∠1=∠3(等量代换).
所以a∥b(同位角相等,两直线平行).
因此∠4=∠5(两直线平行,同位角相等).
例题讲解
A
C
E
F
2
3
B
1
D
例3 如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
【解析】∠3=55°,AB∥CD.
因为∠1=∠2= 55°,
∠3 = ∠2,
所以∠3 =∠1= 55° ,
所以AB∥CD.
(对顶角相等)
(同位角相等,两直线平行)
随堂演练
C
C
随堂演练
平行
同位角相等,两直线平行
50
130
4.如图,哪两个角相等能判定直线AB∥CD?
D
B
4
3
1
4
3
2
A
C
随堂演练
5.如图,∠A=∠BCE,CE平分∠BCD,那么CE与AB的位置关系如何?为什么?
解:CE∥AB.理由:
∵CE平分∠BCD(已知),
∴∠ECD=∠BCE
(角平分线的定义).
又∵∠A=∠BCE(已知),
∴∠A=∠ECD(等量代换),
∴CE∥AB(同位角相等,两直线平行)
随堂演练
6.如图,已知∠ADE=∠B,则∠C+∠CED=( )
A.150° B.160° C.170° D.180°
7.如图,∠1=∠2,∠3=80°,则∠4=( )
A.80° B.70° C.60° D.50°
D
A
随堂演练
8.如图,∠1=∠2,∠3=40°,则∠4等于( )
A.120° B.130° C.140° D.40°
9.如图,已知∠1=∠2=∠3=62°,则∠4=____.
C
118°
随堂演练
10.如图,∠1=∠2=60°,ED平分∠BEF,试说明:AB∥CD.
解:∵ED平分∠BEF
∠2=60°(已知)
∴∠BEF=2∠2=120°
∴∠BEG=180°-∠BEF=60°(邻补角的定义)
∵∠1=60°(已知)
∴∠BEG=∠1(等量代换)
∴AB∥CD(同位角相等,两直线平行)
课后小结
【归纳总结】
1、平行线的性质与判定的区别
平行线的判定是“角的数量关系确定直线的位置关系”,
平行线的性质是“直线的位置关系确定角的数量关系”.
2、平行线的第一个判定方法:
同位角相等,两直线平行。
4.4 第1课时 平行线的判定方法1
情景引入
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
情景引入
(1)平面内两条直线的位置关系有几种?
(2)怎样过已知直线外一点画已知直线的平行线?
相交与平行
思考
获取新知
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
获取新知
1
a
b
.
P
2
如何画平行线?
∠1与∠2具有什么样的位置关系?
把图中的直线 a ,b看成被直尺边所截,那么在画图过程中,什么角始终保持相等?
由此你能发现画两直线平行方法的依据吗?
刚才的画法中,三角板起着什么作用?
1
获取新知
平行线的判定方法1
简单说成:同位角相等,两直线平行.
何言
几语
(同位角相等,两直线平行)
∵∠1=∠2,
∴AB∥CD.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
例题讲解
解 因为∠1+∠2 =180°,
例1 如图,直线AB,CD被直线EF所截,∠1+∠2=180°,AB与CD平行吗? 为什么?
所以AB∥CD(同位角相等,两直线平行).
所以∠2=∠3.
而∠3 是∠1的补角,
即∠1+∠3=180°,
例题讲解
解 因为∠1=∠2(已知),
例2 如图,直线a, b被直线c,d所截,∠1=∠2,说明为什么∠4=∠5.
∠2=∠3 (对顶角相等),
所以∠1=∠3(等量代换).
所以a∥b(同位角相等,两直线平行).
因此∠4=∠5(两直线平行,同位角相等).
例题讲解
A
C
E
F
2
3
B
1
D
例3 如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
【解析】∠3=55°,AB∥CD.
因为∠1=∠2= 55°,
∠3 = ∠2,
所以∠3 =∠1= 55° ,
所以AB∥CD.
(对顶角相等)
(同位角相等,两直线平行)
随堂演练
C
C
随堂演练
平行
同位角相等,两直线平行
50
130
4.如图,哪两个角相等能判定直线AB∥CD?
D
B
4
3
1
4
3
2
A
C
随堂演练
5.如图,∠A=∠BCE,CE平分∠BCD,那么CE与AB的位置关系如何?为什么?
解:CE∥AB.理由:
∵CE平分∠BCD(已知),
∴∠ECD=∠BCE
(角平分线的定义).
又∵∠A=∠BCE(已知),
∴∠A=∠ECD(等量代换),
∴CE∥AB(同位角相等,两直线平行)
随堂演练
6.如图,已知∠ADE=∠B,则∠C+∠CED=( )
A.150° B.160° C.170° D.180°
7.如图,∠1=∠2,∠3=80°,则∠4=( )
A.80° B.70° C.60° D.50°
D
A
随堂演练
8.如图,∠1=∠2,∠3=40°,则∠4等于( )
A.120° B.130° C.140° D.40°
9.如图,已知∠1=∠2=∠3=62°,则∠4=____.
C
118°
随堂演练
10.如图,∠1=∠2=60°,ED平分∠BEF,试说明:AB∥CD.
解:∵ED平分∠BEF
∠2=60°(已知)
∴∠BEF=2∠2=120°
∴∠BEG=180°-∠BEF=60°(邻补角的定义)
∵∠1=60°(已知)
∴∠BEG=∠1(等量代换)
∴AB∥CD(同位角相等,两直线平行)
课后小结
【归纳总结】
1、平行线的性质与判定的区别
平行线的判定是“角的数量关系确定直线的位置关系”,
平行线的性质是“直线的位置关系确定角的数量关系”.
2、平行线的第一个判定方法:
同位角相等,两直线平行。
