人教版数学七年级上册3.4.2销售中的盈亏问题课件(18张PPT)
文档属性
| 名称 | 人教版数学七年级上册3.4.2销售中的盈亏问题课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 482.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 19:53:32 | ||
图片预览






文档简介
应用一元一次方程
——“希望工程”义演
自我超越 止于至善
学习目标
1、 借助表格分析复杂问题中的数量关系,从而建立方程解决实际问题,培养分析问题、解决问题的能力,进一步体会方程模型的作用.(重点)
2、培养应用数学知识的能力,增强探究、推理能力;培养数学兴趣,发展逻辑思维能力,并能应用数学解决日常生活中的问题.(难点)
预习成果展示
票款=票价×张数
总票数=学生票数+成人票数
总票款=学生票数×学生票价+成人票数×成人票价
【总结】列方程的依据是题目的_________,所以找准题目的等量关系是列方程的关键.
等量关系
诊断效果
(打“√”或“×”)
已知应用题:“某幼儿园给几个小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则差2个.求苹果有多少个”
(1)苹果数=小朋友的人数×3+1.( )
(2)苹果数=小朋友的人数×4+2.( )
(3)苹果数=小朋友的人数×4-2.( )
(4)该题目中的等量关系是苹果的数量.( )
√
√
√
×
例、某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款6950元,成人票和学生票各售出多少张?
典例探究
想一想:
在以上提供的信息中,包含哪些等量关系?
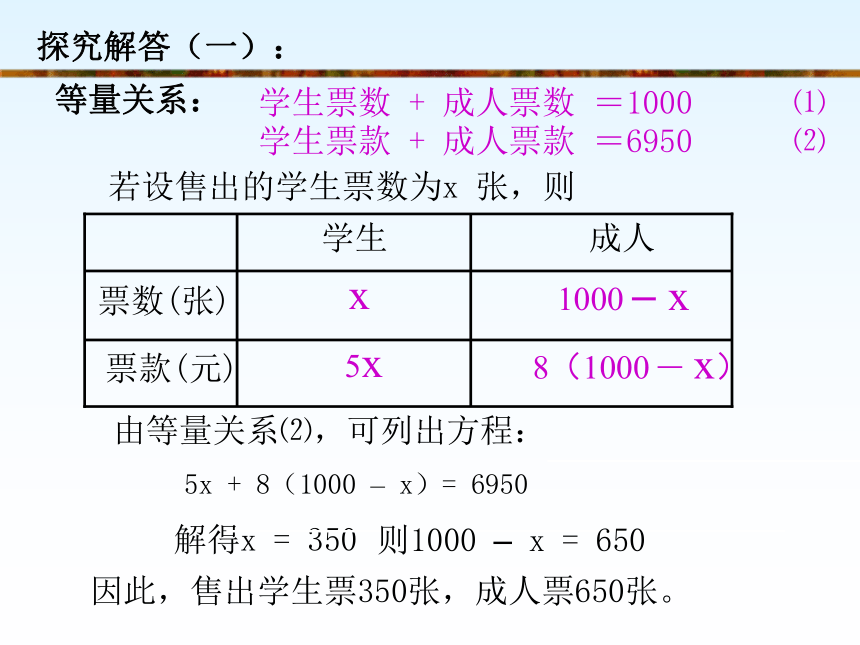
学生票数 + 成人票数 =1000 ⑴
学生票款 + 成人票款 =6950 ⑵
等量关系:
思路点拨
学生票数 + 成人票数 =1000 ⑴
学生票款 + 成人票款 =6950 ⑵
等量关系:
票款(元)
票数(张)
成人
学生
x
1000 – x
5x
8(1000 – x)
由等量关系⑵,可列出方程:
解得x = 350
则1000 – x = 650
因此,售出学生票350张,成人票650张。
5x + 8(1000 – x)= 6950
探究解答(一):
若设售出的学生票数为x 张,则
若设所得的学生票款为y 元,则
票款(元)
票数(张)
成人
学生
y
6950 – y
6950 – y
8
y
5
由⑴,可列出方程:
解得
y = 1750
因此,售出学生票350张,成人票650张。
= 1000
y
5
6950 – y
8
+
,则
1750÷5 = 350
探究解答(二):
学生票数 + 成人票数 =1000 ⑴
学生票款 + 成人票款 =6950 ⑵
等量关系:
列表格如下:
如果原问题中票价和售出的总票数都不变,那么售出1000张票所得票款可能是6930元吗?为什么?
解:设学生票售出x张,则成人票售出(1000–x)张, 根据题意得 5x + 8(1000–x)= 6930
5x + 8000–8x= 6930
-3x= -1070,
x=
1070
3
X的值不符合生活实际,所以总票款不可能是6930元。
想一想:
知识点 含两个等量关系问题
【例】列方程解应用题:
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
针对训练:
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?
(1)设去了x个成人,则去了(12-x)个学生,根据爸爸说的话,可确定相等关系为:成人的票价+学生的票价=400元,据此列方程求解.
思路点拨
(2)计算团体票所需费用,和400元比较即可求解.
(1)设去了x个成人,则去了(12-x)个学生,
由题意得
40x+20(12-x)=400,
解方程得x=8,12-x=4.
答:小明他们一共去了8个成人,4个学生.
自主解答
(2)若按团体票购票:16×40×0.6=384.
因为384<400,所以按团
体票购票更省钱.
解含两个等量关系问题“三步法”
总结提升
题组:含两个等量关系问题
1.A厂库存钢材100吨,每月用去15吨;B厂库存钢材82吨,每月用去9吨.若经过x个月后,两厂库存钢材相等,则x=( )
A.3 B.5 C.2 D.4
【解析】选A.题目中的相等关系是经过x个月后,两厂库存钢材相等.
A厂经过x个月后库存钢材为100-15x;
B厂经过x个月后库存钢材为82-9x.根据题意可列方程100-15x=82-9x,解得:x=3.
2.一张试卷共有25道题,若做对1题得4分,做错1题扣1分,小明做了全部试题只得了70分,那么小明做对了( )
A.17道 B.18道 C.19道 D.20道
【解析】选C.设小明做对了x道,则做错了(25-x)道,
根据题意
得:4x-(25-x)×1=70,
解方程得:x=19.
3.甲种电影票每张20元,乙种电影票每张15元,若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了 张.
【解析】设购买甲种电影票x张,则购买乙种电影票(40-x)张,
根据题意得20x+15(40-x)=700,解得x=20.
答案:20
4.食堂存煤若干,原来每天烧3吨,用去15吨后改进设备,耗煤量每天降为原来的一半,结果多烧10天,则原有煤量多少吨.
【解析】设原有煤量为x吨,改进设备后用煤量为(x-15)吨,
由题意得: ,解方程得x=45,
答:原有煤量为45吨.
5.顺安旅行社组织200人到怀集和德庆旅游,到德庆的人数是到怀集的人数的2倍少1人,到两地旅游的人数各是多少人?
【解析】设到怀集旅游的人数为x人,则到德庆旅游的人数为(2x-1)人,根据题意得出:x+(2x-1)=200,解方程得:x=67,
则到德庆旅游的人数为:2x-1=133(人).
答:到怀集和德庆旅游的人数各是67人,133人.
讨论
说一说这节课的收获!
——“希望工程”义演
自我超越 止于至善
学习目标
1、 借助表格分析复杂问题中的数量关系,从而建立方程解决实际问题,培养分析问题、解决问题的能力,进一步体会方程模型的作用.(重点)
2、培养应用数学知识的能力,增强探究、推理能力;培养数学兴趣,发展逻辑思维能力,并能应用数学解决日常生活中的问题.(难点)
预习成果展示
票款=票价×张数
总票数=学生票数+成人票数
总票款=学生票数×学生票价+成人票数×成人票价
【总结】列方程的依据是题目的_________,所以找准题目的等量关系是列方程的关键.
等量关系
诊断效果
(打“√”或“×”)
已知应用题:“某幼儿园给几个小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则差2个.求苹果有多少个”
(1)苹果数=小朋友的人数×3+1.( )
(2)苹果数=小朋友的人数×4+2.( )
(3)苹果数=小朋友的人数×4-2.( )
(4)该题目中的等量关系是苹果的数量.( )
√
√
√
×
例、某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款6950元,成人票和学生票各售出多少张?
典例探究
想一想:
在以上提供的信息中,包含哪些等量关系?
学生票数 + 成人票数 =1000 ⑴
学生票款 + 成人票款 =6950 ⑵
等量关系:
思路点拨
学生票数 + 成人票数 =1000 ⑴
学生票款 + 成人票款 =6950 ⑵
等量关系:
票款(元)
票数(张)
成人
学生
x
1000 – x
5x
8(1000 – x)
由等量关系⑵,可列出方程:
解得x = 350
则1000 – x = 650
因此,售出学生票350张,成人票650张。
5x + 8(1000 – x)= 6950
探究解答(一):
若设售出的学生票数为x 张,则
若设所得的学生票款为y 元,则
票款(元)
票数(张)
成人
学生
y
6950 – y
6950 – y
8
y
5
由⑴,可列出方程:
解得
y = 1750
因此,售出学生票350张,成人票650张。
= 1000
y
5
6950 – y
8
+
,则
1750÷5 = 350
探究解答(二):
学生票数 + 成人票数 =1000 ⑴
学生票款 + 成人票款 =6950 ⑵
等量关系:
列表格如下:
如果原问题中票价和售出的总票数都不变,那么售出1000张票所得票款可能是6930元吗?为什么?
解:设学生票售出x张,则成人票售出(1000–x)张, 根据题意得 5x + 8(1000–x)= 6930
5x + 8000–8x= 6930
-3x= -1070,
x=
1070
3
X的值不符合生活实际,所以总票款不可能是6930元。
想一想:
知识点 含两个等量关系问题
【例】列方程解应用题:
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
针对训练:
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?
(1)设去了x个成人,则去了(12-x)个学生,根据爸爸说的话,可确定相等关系为:成人的票价+学生的票价=400元,据此列方程求解.
思路点拨
(2)计算团体票所需费用,和400元比较即可求解.
(1)设去了x个成人,则去了(12-x)个学生,
由题意得
40x+20(12-x)=400,
解方程得x=8,12-x=4.
答:小明他们一共去了8个成人,4个学生.
自主解答
(2)若按团体票购票:16×40×0.6=384.
因为384<400,所以按团
体票购票更省钱.
解含两个等量关系问题“三步法”
总结提升
题组:含两个等量关系问题
1.A厂库存钢材100吨,每月用去15吨;B厂库存钢材82吨,每月用去9吨.若经过x个月后,两厂库存钢材相等,则x=( )
A.3 B.5 C.2 D.4
【解析】选A.题目中的相等关系是经过x个月后,两厂库存钢材相等.
A厂经过x个月后库存钢材为100-15x;
B厂经过x个月后库存钢材为82-9x.根据题意可列方程100-15x=82-9x,解得:x=3.
2.一张试卷共有25道题,若做对1题得4分,做错1题扣1分,小明做了全部试题只得了70分,那么小明做对了( )
A.17道 B.18道 C.19道 D.20道
【解析】选C.设小明做对了x道,则做错了(25-x)道,
根据题意
得:4x-(25-x)×1=70,
解方程得:x=19.
3.甲种电影票每张20元,乙种电影票每张15元,若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了 张.
【解析】设购买甲种电影票x张,则购买乙种电影票(40-x)张,
根据题意得20x+15(40-x)=700,解得x=20.
答案:20
4.食堂存煤若干,原来每天烧3吨,用去15吨后改进设备,耗煤量每天降为原来的一半,结果多烧10天,则原有煤量多少吨.
【解析】设原有煤量为x吨,改进设备后用煤量为(x-15)吨,
由题意得: ,解方程得x=45,
答:原有煤量为45吨.
5.顺安旅行社组织200人到怀集和德庆旅游,到德庆的人数是到怀集的人数的2倍少1人,到两地旅游的人数各是多少人?
【解析】设到怀集旅游的人数为x人,则到德庆旅游的人数为(2x-1)人,根据题意得出:x+(2x-1)=200,解方程得:x=67,
则到德庆旅游的人数为:2x-1=133(人).
答:到怀集和德庆旅游的人数各是67人,133人.
讨论
说一说这节课的收获!
