6.3从统计图分析数据的集中趋势(含答案)
文档属性
| 名称 | 6.3从统计图分析数据的集中趋势(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 17:48:50 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第3章数据分析初步
6.3
从统计图分析数据的集中趋势
【知识清单】
一、统计数据常用的统计图有扇形统计图、折线统计图和条形统计图,分别的画图步骤如下:
1、扇形统计图,扇形统计图一般用在百分比比较明确的数据中,可以清楚的看到占比率;
2、折线统计图,折线统计图一般用在变化规律上,可以清楚的看到数据变化规律;
3、条形统计图,条形统计图一般用在数值对比中,可以看到每条数据的高低大小.
二、平均数、中位数、众数从不同的角度反映了一组数据集中趋势,其中算术平均数:
(x1+x2++xn);
加权平均数:()
(其中f1+f2++fk=n);
中位数:将一组数据按大小
(从小到大或从大到小)顺序排列,处于中间位置的一个数据(当数据个数为奇数时)或最中间两个数的平均数(当数据个数为偶数时)叫做这组数据的中位数;
众数:一组数据中出现次数最多的那个数据叫做这组数据的众数.
【经典例题】
例题1、某校开展“同读一本书,共圆一个梦”为山区学生捐书活动中,九年级(1)班50名同学的捐书本数如图所示,求这个班学生捐书本数的平均数、
中位数和众数.
【考点】从统计图分析数据的集中趋势.
【分析】要求平均数只要求出数据之和再除以总个数即可;
对于中位数,因图上是按顺序排列的,所以只要找出中间的两
个数再求平均数即可;对于众数可由条形统计图中出现频率最
大或条形最高的数据写出即可.平均数、中位数与众数不同角
度描述了一组数据的集中趋势.
【解答】平均数为
(本);
中位数应是第25和26两个数的平均数,
而第25和第26两数分别为6和7,所以中位数为
(本);
捐7本的人数为23人,人数最多所以众数为7本.
【点评】本题主要考查条形统计图、加权平均数的计算方法以及中位数和众数的概念,根据条形统计图得出数据,熟悉加权平均数的计算方法是解题的关键.
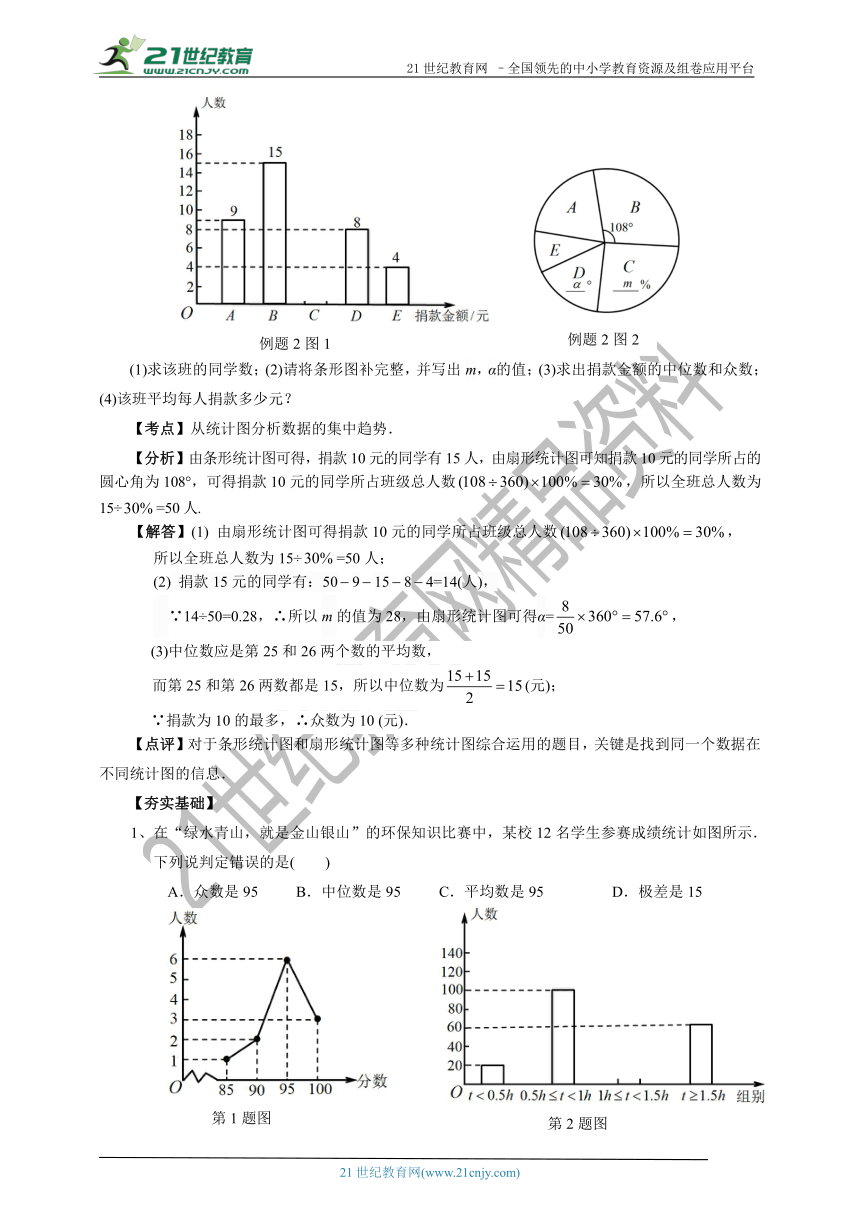
例题2、2008年5月12日,四川省汶川县发生了8.0级的特大地震,全国人民纷纷向灾区伸出了援助之手,某中学八年级(1)班在向“地震灾区献爱心”的捐款活动中积极踊跃,班委会将该班同学捐款情况制作了不完整的条形统计图1和扇形统计图2.
其中A:捐款5元;B:捐款10元;C:捐款15元;D:捐款20元;E:捐款25元.
(1)求该班的同学数;(2)请将条形图补完整,并写出m,α的值;(3)求出捐款金额的中位数和众数;(4)该班平均每人捐款多少元?
【考点】从统计图分析数据的集中趋势.
【分析】由条形统计图可得,捐款10元的同学有15人,由扇形统计图可知捐款10元的同学所占的圆心角为108°,可得捐款10元的同学所占班级总人数,所以全班总人数为15÷=50人.
【解答】(1)
由扇形统计图可得捐款10元的同学所占班级总人数,
所以全班总人数为15÷=50人;
(2)
捐款15元的同学有:5091584=14(人),
∵14÷50=0.28,∴所以m的值为28,由扇形统计图可得α=,
(3)中位数应是第25和26两个数的平均数,
而第25和第26两数都是15,所以中位数为(元);
∵捐款为10的最多,∴众数为10
(元).
【点评】对于条形统计图和扇形统计图等多种统计图综合运用的题目,关键是找到同一个数据在不同统计图的信息.
【夯实基础】
1、在“绿水青山,就是金山银山”的环保知识比赛中,某校12名学生参赛成绩统计如图所示.
下列说判定错误的是( )
A.众数是95
B.中位数是95
C.平均数是95
D.极差是15
2、国家规定“中小学生每天在校体育活动时间不低于1小时”.某市相关调研部门就“学生每天在校体育活动时间是多少?”的问题随机调查了全市不同类型的学校的300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,则下列结论不正确的是(
)
A.1h≤t<1.5h组的人数是120
B.本次调查数据的中位数落在0.5h≤t<1h组内
C.本次调查数据的众数落在1h≤t<1.5h组内
D.若该市约有36000名初中学生,其中达国家规定体育活动时间的人约有21600人.
3、李大伯在承包的荒山上种植了1500棵板栗树,今年开始结果,到了收获的季节,李大伯从中任意采摘了10棵树上的板栗,分别称得每棵树的产量(单位:千克)如下表:这组数据的中位数为m,1500棵板栗的总产量约为n,则m,n分别是( )
序号
1
2
3
4
5
6
7
8
9
10
产量
24
21
22
27
28
24
26
22
29
31
A.24,38100
B.25,38100
C.27,3810
D.25,3810
4、老李家1月至12月的用电量统计如图所示,这组数据的众数和中位数分别是(???
)
A.30和
20
?B.30和22.5
?C.25和25?
D.25和30
5、某班生活委员对本班学生一周帮家做家务的时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周做家务时间的中位数是
小时.
6、如图是某班学生的一次数学测验的扇形统计图和与之对应的统计表(分值为100分),
成绩
95
90
人数
a
16
成绩
85
75
人数
b
2
则学生数学成绩的平均数
,中位数
,众数
,a=
,b=
,,x=
,y=
.
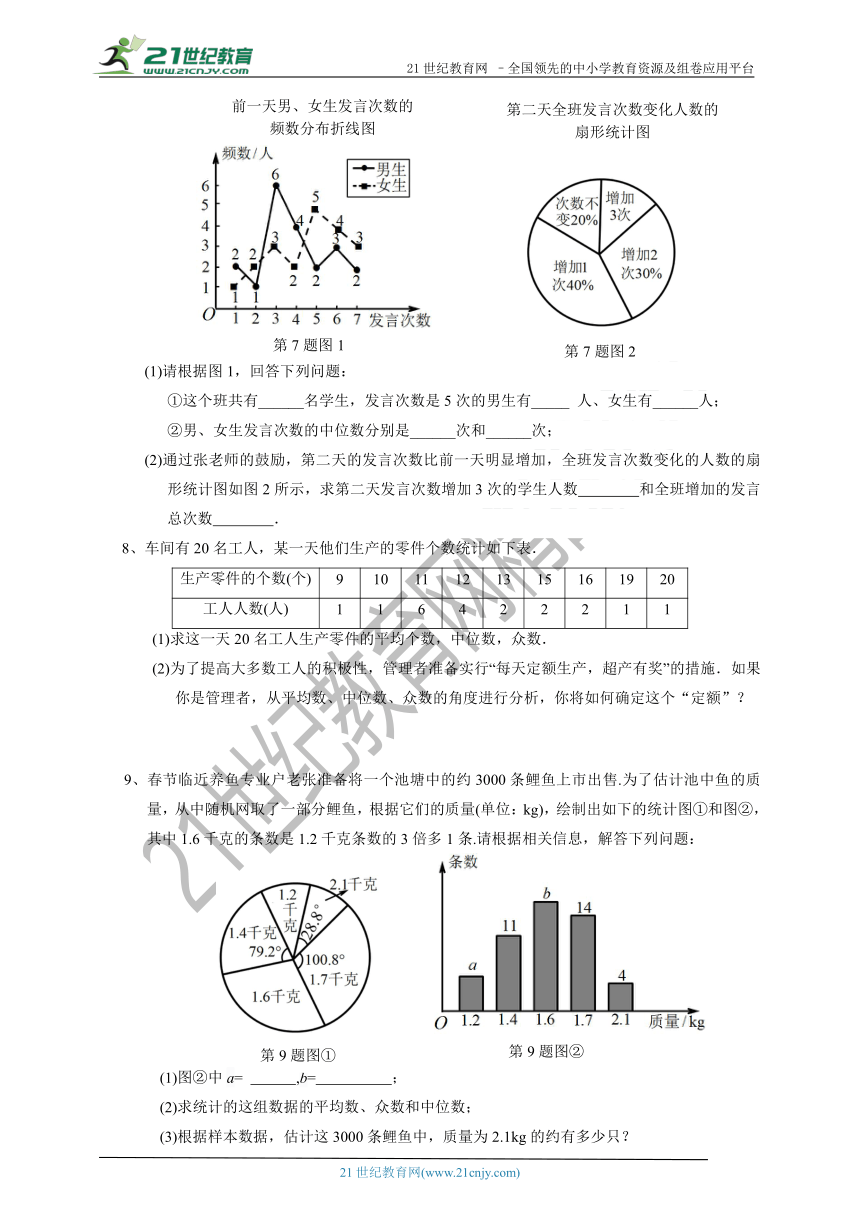
7、班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1)和扇形图(图2).
(1)请根据图1,回答下列问题:
①这个班共有______名学生,发言次数是5次的男生有_____
人、女生有______人;
②男、女生发言次数的中位数分别是______次和______次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数
和全班增加的发言总次数
.
8、车间有20名工人,某一天他们生产的零件个数统计如下表.
生产零件的个数(个)
9
10
11
12
13
15
16
19
20
工人人数(人)
1
1
6
4
2
2
2
1
1
(1)求这一天20名工人生产零件的平均个数,中位数,众数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
9、春节临近养鱼专业户老张准备将一个池塘中的约3000条鲤鱼上市出售.为了估计池中鱼的质量,从中随机网取了一部分鲤鱼,根据它们的质量(单位:kg),绘制出如下的统计图①和图②,其中1.6千克的条数是1.2千克条数的3倍多1条.请根据相关信息,解答下列问题:
(1)图②中a=
,b=
;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这3000条鲤鱼中,质量为2.1kg的约有多少只?
【提优特训】
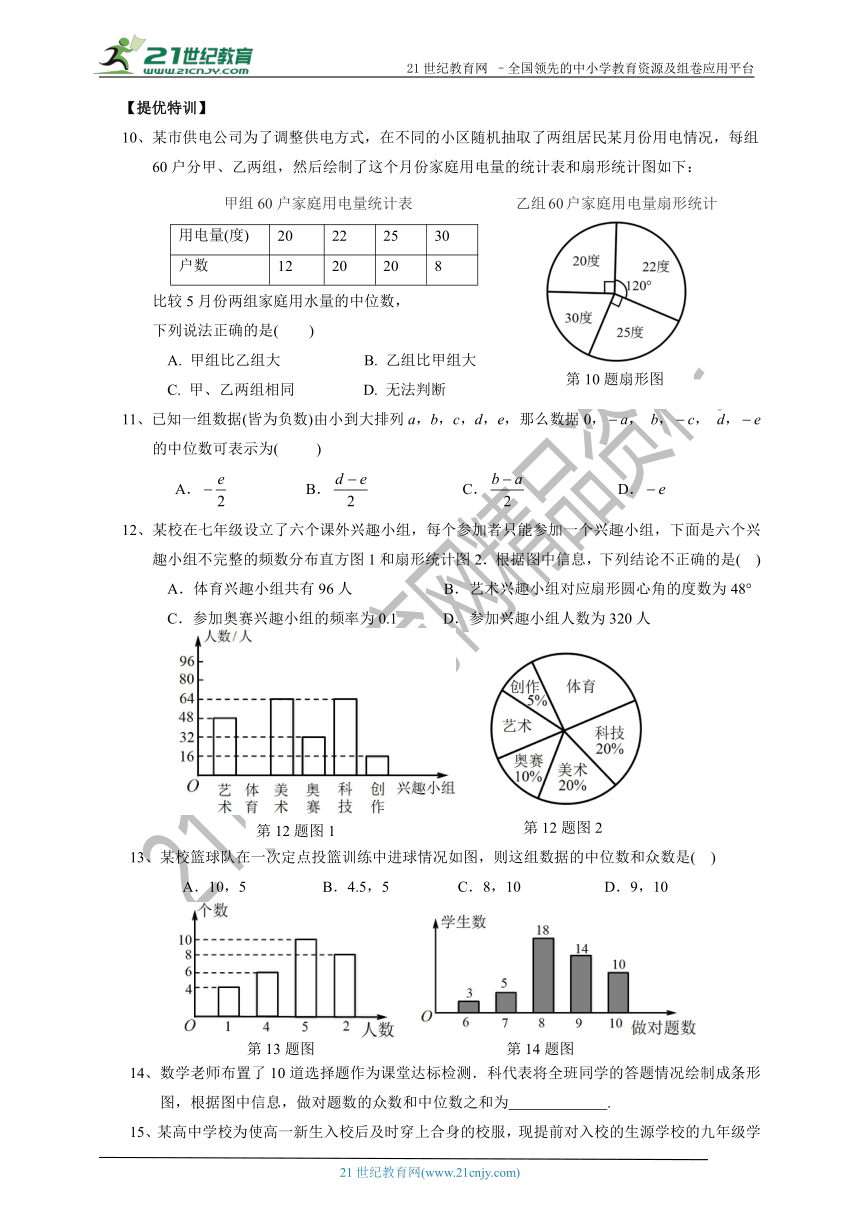
10、某市供电公司为了调整供电方式,在不同的小区随机抽取了两组居民某月份用电情况,每组
60户分甲、乙两组,然后绘制了这个月份家庭用电量的统计表和扇形统计图如下:
用电量(度)
20
22
25
30
户数
12
20
20
8
比较5月份两组家庭用水量的中位数,
下列说法正确的是( )
A.
甲组比乙组大
B.
乙组比甲组大
C.
甲、乙两组相同
D.
无法判断
11、已知一组数据(皆为负数)由小到大排列a,b,c,d,e,那么数据0,a,
b,c,
d,e
的中位数可表示为(
)
A.
B.
C.
D.
12、某校在七年级设立了六个课外兴趣小组,每个参加者只能参加一个兴趣小组,下面是六个兴趣小组不完整的频数分布直方图1和扇形统计图2.根据图中信息,下列结论不正确的是(
)
A.体育兴趣小组共有96人
B.艺术兴趣小组对应扇形圆心角的度数为48°
C.参加奥赛兴趣小组的频率为0.1
D.参加兴趣小组人数为320人
13、某校篮球队在一次定点投篮训练中进球情况如图,则这组数据的中位数和众数是(
)
A.10,5
B.4.5,5
C.8,10
D.9,10
14、数学老师布置了10道选择题作为课堂达标检测.科代表将全班同学的答题情况绘制成条形图,根据图中信息,做对题数的众数和中位数之和为
.
15、某高中学校为使高一新生入校后及时穿上合身的校服,现提前对入校的生源学校的九年级学生随机抽查摸底,并根据调查结果绘制了如图两个不完整的统计图1和图2(校服型号以身高作为标准,共分为6种型号).
根据以上信息进行填空:
(1)此次抽查的学生
名,其中穿175型校服的学生
名.
(2)在扇形统计图中185型校服所占的百分比为
;
(3)抽取的学生所穿校服型号的众数
和中位数
.
16、某株心算训练班为了解参训同学的年龄情况,根据参训同学的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息填空:
(1)本次接受调查的参训同学人数为???
??,图①中a的值为??
???,
b的值为???
????;???
(2)求统计的这组跳水运动员年龄数据的平均数
、众数
中位数
.
17、某校为了了解八年级一周在家做家务的时间(单位:h),随机抽查了该学校八年级a名同学,对其每周平均做家务时间进行统计,绘制了如下条形统计图(图1)和扇形统计图(图2):
(1)根据以上信息回答下列问题:
①求a的值;②求扇形统计图中做家务的时间为5小时的扇形圆心角的度数;
③补全条形统计图.
(2)求这组数据的众数、中位数,求出这组数据的平均数.
18、某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
设销售员的月销售额为x(单位:万元).销售部规定:当x<16时,为“不称职”,
当
16≤x<20时为“基本称职”,当
20≤x<25时为“称职”,当
x≥25时为“优秀”.
根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一般人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由。
【中考链接】
19、(2020?温州)
山茶花是温州市的市花,品种多样,“金心大红”是其中的一种.某兴趣小组对30
株“金心大红”的花径进行测量、记录,统计如下表.
株数(株)
7
9
12
2
花径(cm)
6.5
6.6
6.7
6.8
这批“金心大红”花径的众数为()
A
.6.5cm
B.
6.
6cm
C.
6.7cm
D.
6.8cm
20、(2020?山东聊城)为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自
不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是(
)?
成绩/分
84
88
92
96
100
人数/人
2
4
9
10
5
?A.92分,96分
B.94分,96分
C.96分,96分?
D.96分,100分
21、(2020?金华、丽水)1,2,4,5,3的中位数是
.
22、(2020?江苏泰州)今年6月6日是第25个全国爱眼日,某校从八年级随机抽取50名学生进行
了视力调查,并根据视力值绘制成统计图(如图),这50名学生视力的中位数所在范围是
.
23、(2020?吉林长春)空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、
三级轻度污染、四级中度污染、五级重度污染六级严重污染.级别越高,说明污染的情况越
严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图
是长春市从2014年到2019年的空气质量级别天数的统计图表.
?2014﹣2019年长春市空气质量级别天数统计表
空气质量级别
天数
年份
优
良
轻度污染
中度污染
重度污染
严重污染
2014
30
215
73
28
13
6
2015
43
193
87
19
15
8
2016
51
237
58
15
5
0
2017
65
211
62
16
9
2
2018
123
202
39
0
1
0
2019
126
180
38
16
5
0
?2014﹣2019年长春市空气质量为“达标”和“优”的天数折线统计图:
根据上面的统计图表回答下列问题:
?
(1)长春市从2014年到2019年空气质量为“达标”的天数最多的是
年.
(2)长春市从2014年到2019年空气质量为“重度污染”的天数的中位数为
天,
平均数为
天.
?
(3)长春市从2015年到2019年,和前一年相比,空气质量为“优”的天数增加最多的是
年,这一年空气质量为“优”的天数的年增长率约为
(精确到1%)(空气质量为“优”的天数的增长率=×100%).
?
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.
参考答案
1、C
2、B
3、B
4、C
5、6
6、89.5,90,90,12,10,40%,5%
.
7、(1)
40,2,5②4,5(2)
4,52
10、C
11、A
12、B
13、C
14、16
15、(1)
50,10
(2)
4%
(3)
165或170,
170
16、
(1)???40,?25,10
(2)
11.95,12,12
19、C
20、B
21、3
22、
4.65﹣4.95
8、车间有20名工人,某一天他们生产的零件个数统计如下表.
生产零件的个数(个)
9
10
11
12
13
15
16
19
20
工人人数(人)
1
1
6
4
2
2
2
1
1
(1)求这一天20名工人生产零件的平均个数,中位数,众数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
解:(1)×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)
=13(个);
答:这一天20名工人生产零件的平均个数为13个;
(2)将这些数据从小到大排列,中间两个数都是12,因此中位数为=12(个);
又数据11出现6次,次数最多,所以这组数据的众数为11个,
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,6人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性;
∴定额为11个时,有利于提高大多数工人的积极性.
9、春节临近养鱼专业户老张准备将一个池塘中的约3000条鲤鱼上市出售.为了估计池中鱼的质量,从中随机网取了一部分鲤鱼,根据它们的质量(单位:kg),绘制出如下的统计图①和图②,其中1.6千克的条数是1.2千克条数的3倍多1条.请根据相关信息,解答下列问题:
(1)图②中a=
,b=
;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这3000条鲤鱼中,质量为2.1kg的约有多少只?
解:(1)由扇形图质量为1.4千克的圆心角为79.2°,
占
因为1.4千克在条形图中为11条,
所以11÷22%=50(条),
所以网取的鲤鱼的条数为50条;
a+b=5011144=21,
根据题意,得
解得
(2)观察条形统计图,
∵,
∴这组数据的平均数是1.584.
∵在这组数据中,1.6出现了16次,出现的次数最多,
∴这组数据的众数为1.6.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.6,
有,
∴这组数据的中位数为1.6.
(3)∵在所抽取的样本中,质量为2.1kg的数量占8%.
∴由样本数据,估计这3000条鲤鱼中,
有3000×8%=240(条)..
∴这3000条鲤鱼中,质量为2.1kg的约有240条.
17、某校为了了解八年级一周在家做家务的时间(单位:h),随机抽查了该学校八年级a名同学,对其每周平均做家务时间进行统计,绘制了如下条形统计图(图1)和扇形统计图(图2):
(1)根据以上信息回答下列问题:
①求a的值;②求扇形统计图中做家务的时间为5小时的扇形圆心角的度数;
③补全条形统计图.
(2)求这组数据的众数、中位数,求出这组数据的平均数.
解:(1)①∵课外阅读时间为3小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为,
∵课外阅读时间为3小时的有25人,
∴a=25÷=100;②依题意得:
③第三小组的频数为:10015252010=30,
补全条形统计图为:
(2)∵课外阅读时间为4小时的30人,最多,
∴众数为
4小时;
∵共100人,中位数应该是第50和第51人的平均数,且第50和第51人阅读时间均为4
小时,∴中位数为4小时;
平均数为:=3.85小时.
18、某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
设销售员的月销售额为x(单位:万元).销售部规定:当x<16时,为“不称职”,
当
16≤x<20时为“基本称职”,当
20≤x<25时为“称职”,当
x≥25时为“优秀”.
根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一般人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由。
解:(1)依题可得:
“不称职”人数为:2+2=4(人),
“基本称职”人数为:2+3+3+2=10(人),
“称职”人数为:4+5+4+3+4=20(人),
∴总人数为:20÷50%=40(人),
∴“不称职”百分比:a=4÷40=10%,
“基本称职”百分比:b=10÷40=25%,
“优秀”百分比:d=110%25%50%=15%,
∴“优秀”人数为:40×15%=6(人),
∴得26分的人数为:6211=2(人),
补全统计图如图所示:
(2)由折线统计图可知:“称职”20万4人,21万5人,22万4人,23万3人,24万4人,
“优秀”25万2人,26万2人,27万1人,28万1人;
“称职”的销售员月销售额的中位数为:22万,众数:21万;
“优秀”的销售员月销售额的中位数为:26万,众数:25万和26万;
(3)由(2)知月销售额奖励标准应定为22万.
∵“称职”和“优秀”的销售员月销售额的中位数为:22万,
∴要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定
为22万元.
23、(2020?吉林长春)空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、
三级轻度污染、四级中度污染、五级重度污染六级严重污染.级别越高,说明污染的情况越
严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图
是长春市从2014年到2019年的空气质量级别天数的统计图表.
?2014﹣2019年长春市空气质量级别天数统计表
空气质量级别
天数
年份
优
良
轻度污染
中度污染
重度污染
严重污染
2014
30
215
73
28
13
6
2015
43
193
87
19
15
8
2016
51
237
58
15
5
0
2017
65
211
62
16
9
2
2018
123
202
39
0
1
0
2019
126
180
38
16
5
0
?2014﹣2019年长春市空气质量为“达标”和“优”的天数折线统计图:
根据上面的统计图表回答下列问题:
?
(1)长春市从2014年到2019年空气质量为“达标”的天数最多的是
年.
(2)长春市从2014年到2019年空气质量为“重度污染”的天数的中位数为
天,
平均数为
天.
?
(3)长春市从2015年到2019年,和前一年相比,空气质量为“优”的天数增加最多的是
年,这一年空气质量为“优”的天数的年增长率约为
(精确到1%)(空气质量为“优”的天数的增长率=×100%).
?
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.
解:(1)从折线统计图中“达标”天数的折线的最高点,相应的年份为2018年,
?
故答案为:2018;
?
(2)将这6年的“重度污染”的天数从小到大排列为1,5
,5,9,13,15,处在中间位
置的两个数为5,9,5,9的平均数为,
年的“重度污染”的天数的平均数为=8天,
?
故答案为:7,8;
?
(3)前一年相比,空气质量为“优”的天数增加量为:
?
2015年,4330=13天;
?2016年,5143=8天;
?2017年,6551=14天;
?2018年,12365=58天;
?
2019年,126123=3天,
因此空气质量为“优”的天数增加最多的是2018年,这一年空气质量为“优”的天数的年增长率约为增长率为≈89%,
?
故答案为:2018,89%;
?
(4)从统计表中数据可知,2018年空气质量好,2018年“达标天数”最多,重度污染、中度污染、严重污染的天数最少.
例题2图1
例题1图
甲组60户家庭用电量统计表
第二天全班发言次数变化人数的
扇形统计图
第15图2
例题2图2
第1题图
第15图1
第5题图
乙组60户家庭用电量扇形统计图
第6题表
第9题图①
第7题图1
前一天男、女生发言次数的
频数分布折线图
第2题图
扇形统计图
条形统计图
第4题图
第6题扇形图
第7题图2
第9题图②
第10题扇形图
第12题图1
第12题图2
第13题图
第14题图
第16题图①
第16题图②
第17题图1
第17题图2
第23题表
第23题图
第9题图①
第9题图②
第17题图1
第17题图2
第17题补全图
第18题折线图
第18题扇形图
第18题折线图
第18题扇形图
第18题折线补全图
第18题扇形补全图
第23题表
第23题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
浙江版八年级数学下册第3章数据分析初步
6.3
从统计图分析数据的集中趋势
【知识清单】
一、统计数据常用的统计图有扇形统计图、折线统计图和条形统计图,分别的画图步骤如下:
1、扇形统计图,扇形统计图一般用在百分比比较明确的数据中,可以清楚的看到占比率;
2、折线统计图,折线统计图一般用在变化规律上,可以清楚的看到数据变化规律;
3、条形统计图,条形统计图一般用在数值对比中,可以看到每条数据的高低大小.
二、平均数、中位数、众数从不同的角度反映了一组数据集中趋势,其中算术平均数:
(x1+x2++xn);
加权平均数:()
(其中f1+f2++fk=n);
中位数:将一组数据按大小
(从小到大或从大到小)顺序排列,处于中间位置的一个数据(当数据个数为奇数时)或最中间两个数的平均数(当数据个数为偶数时)叫做这组数据的中位数;
众数:一组数据中出现次数最多的那个数据叫做这组数据的众数.
【经典例题】
例题1、某校开展“同读一本书,共圆一个梦”为山区学生捐书活动中,九年级(1)班50名同学的捐书本数如图所示,求这个班学生捐书本数的平均数、
中位数和众数.
【考点】从统计图分析数据的集中趋势.
【分析】要求平均数只要求出数据之和再除以总个数即可;
对于中位数,因图上是按顺序排列的,所以只要找出中间的两
个数再求平均数即可;对于众数可由条形统计图中出现频率最
大或条形最高的数据写出即可.平均数、中位数与众数不同角
度描述了一组数据的集中趋势.
【解答】平均数为
(本);
中位数应是第25和26两个数的平均数,
而第25和第26两数分别为6和7,所以中位数为
(本);
捐7本的人数为23人,人数最多所以众数为7本.
【点评】本题主要考查条形统计图、加权平均数的计算方法以及中位数和众数的概念,根据条形统计图得出数据,熟悉加权平均数的计算方法是解题的关键.
例题2、2008年5月12日,四川省汶川县发生了8.0级的特大地震,全国人民纷纷向灾区伸出了援助之手,某中学八年级(1)班在向“地震灾区献爱心”的捐款活动中积极踊跃,班委会将该班同学捐款情况制作了不完整的条形统计图1和扇形统计图2.
其中A:捐款5元;B:捐款10元;C:捐款15元;D:捐款20元;E:捐款25元.
(1)求该班的同学数;(2)请将条形图补完整,并写出m,α的值;(3)求出捐款金额的中位数和众数;(4)该班平均每人捐款多少元?
【考点】从统计图分析数据的集中趋势.
【分析】由条形统计图可得,捐款10元的同学有15人,由扇形统计图可知捐款10元的同学所占的圆心角为108°,可得捐款10元的同学所占班级总人数,所以全班总人数为15÷=50人.
【解答】(1)
由扇形统计图可得捐款10元的同学所占班级总人数,
所以全班总人数为15÷=50人;
(2)
捐款15元的同学有:5091584=14(人),
∵14÷50=0.28,∴所以m的值为28,由扇形统计图可得α=,
(3)中位数应是第25和26两个数的平均数,
而第25和第26两数都是15,所以中位数为(元);
∵捐款为10的最多,∴众数为10
(元).
【点评】对于条形统计图和扇形统计图等多种统计图综合运用的题目,关键是找到同一个数据在不同统计图的信息.
【夯实基础】
1、在“绿水青山,就是金山银山”的环保知识比赛中,某校12名学生参赛成绩统计如图所示.
下列说判定错误的是( )
A.众数是95
B.中位数是95
C.平均数是95
D.极差是15
2、国家规定“中小学生每天在校体育活动时间不低于1小时”.某市相关调研部门就“学生每天在校体育活动时间是多少?”的问题随机调查了全市不同类型的学校的300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,则下列结论不正确的是(
)
A.1h≤t<1.5h组的人数是120
B.本次调查数据的中位数落在0.5h≤t<1h组内
C.本次调查数据的众数落在1h≤t<1.5h组内
D.若该市约有36000名初中学生,其中达国家规定体育活动时间的人约有21600人.
3、李大伯在承包的荒山上种植了1500棵板栗树,今年开始结果,到了收获的季节,李大伯从中任意采摘了10棵树上的板栗,分别称得每棵树的产量(单位:千克)如下表:这组数据的中位数为m,1500棵板栗的总产量约为n,则m,n分别是( )
序号
1
2
3
4
5
6
7
8
9
10
产量
24
21
22
27
28
24
26
22
29
31
A.24,38100
B.25,38100
C.27,3810
D.25,3810
4、老李家1月至12月的用电量统计如图所示,这组数据的众数和中位数分别是(???
)
A.30和
20
?B.30和22.5
?C.25和25?
D.25和30
5、某班生活委员对本班学生一周帮家做家务的时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周做家务时间的中位数是
小时.
6、如图是某班学生的一次数学测验的扇形统计图和与之对应的统计表(分值为100分),
成绩
95
90
人数
a
16
成绩
85
75
人数
b
2
则学生数学成绩的平均数
,中位数
,众数
,a=
,b=
,,x=
,y=
.
7、班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1)和扇形图(图2).
(1)请根据图1,回答下列问题:
①这个班共有______名学生,发言次数是5次的男生有_____
人、女生有______人;
②男、女生发言次数的中位数分别是______次和______次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数
和全班增加的发言总次数
.
8、车间有20名工人,某一天他们生产的零件个数统计如下表.
生产零件的个数(个)
9
10
11
12
13
15
16
19
20
工人人数(人)
1
1
6
4
2
2
2
1
1
(1)求这一天20名工人生产零件的平均个数,中位数,众数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
9、春节临近养鱼专业户老张准备将一个池塘中的约3000条鲤鱼上市出售.为了估计池中鱼的质量,从中随机网取了一部分鲤鱼,根据它们的质量(单位:kg),绘制出如下的统计图①和图②,其中1.6千克的条数是1.2千克条数的3倍多1条.请根据相关信息,解答下列问题:
(1)图②中a=
,b=
;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这3000条鲤鱼中,质量为2.1kg的约有多少只?
【提优特训】
10、某市供电公司为了调整供电方式,在不同的小区随机抽取了两组居民某月份用电情况,每组
60户分甲、乙两组,然后绘制了这个月份家庭用电量的统计表和扇形统计图如下:
用电量(度)
20
22
25
30
户数
12
20
20
8
比较5月份两组家庭用水量的中位数,
下列说法正确的是( )
A.
甲组比乙组大
B.
乙组比甲组大
C.
甲、乙两组相同
D.
无法判断
11、已知一组数据(皆为负数)由小到大排列a,b,c,d,e,那么数据0,a,
b,c,
d,e
的中位数可表示为(
)
A.
B.
C.
D.
12、某校在七年级设立了六个课外兴趣小组,每个参加者只能参加一个兴趣小组,下面是六个兴趣小组不完整的频数分布直方图1和扇形统计图2.根据图中信息,下列结论不正确的是(
)
A.体育兴趣小组共有96人
B.艺术兴趣小组对应扇形圆心角的度数为48°
C.参加奥赛兴趣小组的频率为0.1
D.参加兴趣小组人数为320人
13、某校篮球队在一次定点投篮训练中进球情况如图,则这组数据的中位数和众数是(
)
A.10,5
B.4.5,5
C.8,10
D.9,10
14、数学老师布置了10道选择题作为课堂达标检测.科代表将全班同学的答题情况绘制成条形图,根据图中信息,做对题数的众数和中位数之和为
.
15、某高中学校为使高一新生入校后及时穿上合身的校服,现提前对入校的生源学校的九年级学生随机抽查摸底,并根据调查结果绘制了如图两个不完整的统计图1和图2(校服型号以身高作为标准,共分为6种型号).
根据以上信息进行填空:
(1)此次抽查的学生
名,其中穿175型校服的学生
名.
(2)在扇形统计图中185型校服所占的百分比为
;
(3)抽取的学生所穿校服型号的众数
和中位数
.
16、某株心算训练班为了解参训同学的年龄情况,根据参训同学的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息填空:
(1)本次接受调查的参训同学人数为???
??,图①中a的值为??
???,
b的值为???
????;???
(2)求统计的这组跳水运动员年龄数据的平均数
、众数
中位数
.
17、某校为了了解八年级一周在家做家务的时间(单位:h),随机抽查了该学校八年级a名同学,对其每周平均做家务时间进行统计,绘制了如下条形统计图(图1)和扇形统计图(图2):
(1)根据以上信息回答下列问题:
①求a的值;②求扇形统计图中做家务的时间为5小时的扇形圆心角的度数;
③补全条形统计图.
(2)求这组数据的众数、中位数,求出这组数据的平均数.
18、某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
设销售员的月销售额为x(单位:万元).销售部规定:当x<16时,为“不称职”,
当
16≤x<20时为“基本称职”,当
20≤x<25时为“称职”,当
x≥25时为“优秀”.
根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一般人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由。
【中考链接】
19、(2020?温州)
山茶花是温州市的市花,品种多样,“金心大红”是其中的一种.某兴趣小组对30
株“金心大红”的花径进行测量、记录,统计如下表.
株数(株)
7
9
12
2
花径(cm)
6.5
6.6
6.7
6.8
这批“金心大红”花径的众数为()
A
.6.5cm
B.
6.
6cm
C.
6.7cm
D.
6.8cm
20、(2020?山东聊城)为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来自
不同年级的30名参赛同学的得分情况如下表所示,这些成绩的中位数和众数分别是(
)?
成绩/分
84
88
92
96
100
人数/人
2
4
9
10
5
?A.92分,96分
B.94分,96分
C.96分,96分?
D.96分,100分
21、(2020?金华、丽水)1,2,4,5,3的中位数是
.
22、(2020?江苏泰州)今年6月6日是第25个全国爱眼日,某校从八年级随机抽取50名学生进行
了视力调查,并根据视力值绘制成统计图(如图),这50名学生视力的中位数所在范围是
.
23、(2020?吉林长春)空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、
三级轻度污染、四级中度污染、五级重度污染六级严重污染.级别越高,说明污染的情况越
严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图
是长春市从2014年到2019年的空气质量级别天数的统计图表.
?2014﹣2019年长春市空气质量级别天数统计表
空气质量级别
天数
年份
优
良
轻度污染
中度污染
重度污染
严重污染
2014
30
215
73
28
13
6
2015
43
193
87
19
15
8
2016
51
237
58
15
5
0
2017
65
211
62
16
9
2
2018
123
202
39
0
1
0
2019
126
180
38
16
5
0
?2014﹣2019年长春市空气质量为“达标”和“优”的天数折线统计图:
根据上面的统计图表回答下列问题:
?
(1)长春市从2014年到2019年空气质量为“达标”的天数最多的是
年.
(2)长春市从2014年到2019年空气质量为“重度污染”的天数的中位数为
天,
平均数为
天.
?
(3)长春市从2015年到2019年,和前一年相比,空气质量为“优”的天数增加最多的是
年,这一年空气质量为“优”的天数的年增长率约为
(精确到1%)(空气质量为“优”的天数的增长率=×100%).
?
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.
参考答案
1、C
2、B
3、B
4、C
5、6
6、89.5,90,90,12,10,40%,5%
.
7、(1)
40,2,5②4,5(2)
4,52
10、C
11、A
12、B
13、C
14、16
15、(1)
50,10
(2)
4%
(3)
165或170,
170
16、
(1)???40,?25,10
(2)
11.95,12,12
19、C
20、B
21、3
22、
4.65﹣4.95
8、车间有20名工人,某一天他们生产的零件个数统计如下表.
生产零件的个数(个)
9
10
11
12
13
15
16
19
20
工人人数(人)
1
1
6
4
2
2
2
1
1
(1)求这一天20名工人生产零件的平均个数,中位数,众数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
解:(1)×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)
=13(个);
答:这一天20名工人生产零件的平均个数为13个;
(2)将这些数据从小到大排列,中间两个数都是12,因此中位数为=12(个);
又数据11出现6次,次数最多,所以这组数据的众数为11个,
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,6人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性;
∴定额为11个时,有利于提高大多数工人的积极性.
9、春节临近养鱼专业户老张准备将一个池塘中的约3000条鲤鱼上市出售.为了估计池中鱼的质量,从中随机网取了一部分鲤鱼,根据它们的质量(单位:kg),绘制出如下的统计图①和图②,其中1.6千克的条数是1.2千克条数的3倍多1条.请根据相关信息,解答下列问题:
(1)图②中a=
,b=
;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这3000条鲤鱼中,质量为2.1kg的约有多少只?
解:(1)由扇形图质量为1.4千克的圆心角为79.2°,
占
因为1.4千克在条形图中为11条,
所以11÷22%=50(条),
所以网取的鲤鱼的条数为50条;
a+b=5011144=21,
根据题意,得
解得
(2)观察条形统计图,
∵,
∴这组数据的平均数是1.584.
∵在这组数据中,1.6出现了16次,出现的次数最多,
∴这组数据的众数为1.6.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.6,
有,
∴这组数据的中位数为1.6.
(3)∵在所抽取的样本中,质量为2.1kg的数量占8%.
∴由样本数据,估计这3000条鲤鱼中,
有3000×8%=240(条)..
∴这3000条鲤鱼中,质量为2.1kg的约有240条.
17、某校为了了解八年级一周在家做家务的时间(单位:h),随机抽查了该学校八年级a名同学,对其每周平均做家务时间进行统计,绘制了如下条形统计图(图1)和扇形统计图(图2):
(1)根据以上信息回答下列问题:
①求a的值;②求扇形统计图中做家务的时间为5小时的扇形圆心角的度数;
③补全条形统计图.
(2)求这组数据的众数、中位数,求出这组数据的平均数.
解:(1)①∵课外阅读时间为3小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为,
∵课外阅读时间为3小时的有25人,
∴a=25÷=100;②依题意得:
③第三小组的频数为:10015252010=30,
补全条形统计图为:
(2)∵课外阅读时间为4小时的30人,最多,
∴众数为
4小时;
∵共100人,中位数应该是第50和第51人的平均数,且第50和第51人阅读时间均为4
小时,∴中位数为4小时;
平均数为:=3.85小时.
18、某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:
设销售员的月销售额为x(单位:万元).销售部规定:当x<16时,为“不称职”,
当
16≤x<20时为“基本称职”,当
20≤x<25时为“称职”,当
x≥25时为“优秀”.
根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一般人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由。
解:(1)依题可得:
“不称职”人数为:2+2=4(人),
“基本称职”人数为:2+3+3+2=10(人),
“称职”人数为:4+5+4+3+4=20(人),
∴总人数为:20÷50%=40(人),
∴“不称职”百分比:a=4÷40=10%,
“基本称职”百分比:b=10÷40=25%,
“优秀”百分比:d=110%25%50%=15%,
∴“优秀”人数为:40×15%=6(人),
∴得26分的人数为:6211=2(人),
补全统计图如图所示:
(2)由折线统计图可知:“称职”20万4人,21万5人,22万4人,23万3人,24万4人,
“优秀”25万2人,26万2人,27万1人,28万1人;
“称职”的销售员月销售额的中位数为:22万,众数:21万;
“优秀”的销售员月销售额的中位数为:26万,众数:25万和26万;
(3)由(2)知月销售额奖励标准应定为22万.
∵“称职”和“优秀”的销售员月销售额的中位数为:22万,
∴要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定
为22万元.
23、(2020?吉林长春)空气质量按照空气质量指数大小分为六个级别,分别为:一级优、二级良、
三级轻度污染、四级中度污染、五级重度污染六级严重污染.级别越高,说明污染的情况越
严重,对人体的健康危害也就越大.空气质量达到一级优或二级良的天气为达标天气,如图
是长春市从2014年到2019年的空气质量级别天数的统计图表.
?2014﹣2019年长春市空气质量级别天数统计表
空气质量级别
天数
年份
优
良
轻度污染
中度污染
重度污染
严重污染
2014
30
215
73
28
13
6
2015
43
193
87
19
15
8
2016
51
237
58
15
5
0
2017
65
211
62
16
9
2
2018
123
202
39
0
1
0
2019
126
180
38
16
5
0
?2014﹣2019年长春市空气质量为“达标”和“优”的天数折线统计图:
根据上面的统计图表回答下列问题:
?
(1)长春市从2014年到2019年空气质量为“达标”的天数最多的是
年.
(2)长春市从2014年到2019年空气质量为“重度污染”的天数的中位数为
天,
平均数为
天.
?
(3)长春市从2015年到2019年,和前一年相比,空气质量为“优”的天数增加最多的是
年,这一年空气质量为“优”的天数的年增长率约为
(精确到1%)(空气质量为“优”的天数的增长率=×100%).
?
(4)你认为长春市从2014年到2019年哪一年的空气质量好?请说明理由.
解:(1)从折线统计图中“达标”天数的折线的最高点,相应的年份为2018年,
?
故答案为:2018;
?
(2)将这6年的“重度污染”的天数从小到大排列为1,5
,5,9,13,15,处在中间位
置的两个数为5,9,5,9的平均数为,
年的“重度污染”的天数的平均数为=8天,
?
故答案为:7,8;
?
(3)前一年相比,空气质量为“优”的天数增加量为:
?
2015年,4330=13天;
?2016年,5143=8天;
?2017年,6551=14天;
?2018年,12365=58天;
?
2019年,126123=3天,
因此空气质量为“优”的天数增加最多的是2018年,这一年空气质量为“优”的天数的年增长率约为增长率为≈89%,
?
故答案为:2018,89%;
?
(4)从统计表中数据可知,2018年空气质量好,2018年“达标天数”最多,重度污染、中度污染、严重污染的天数最少.
例题2图1
例题1图
甲组60户家庭用电量统计表
第二天全班发言次数变化人数的
扇形统计图
第15图2
例题2图2
第1题图
第15图1
第5题图
乙组60户家庭用电量扇形统计图
第6题表
第9题图①
第7题图1
前一天男、女生发言次数的
频数分布折线图
第2题图
扇形统计图
条形统计图
第4题图
第6题扇形图
第7题图2
第9题图②
第10题扇形图
第12题图1
第12题图2
第13题图
第14题图
第16题图①
第16题图②
第17题图1
第17题图2
第23题表
第23题图
第9题图①
第9题图②
第17题图1
第17题图2
第17题补全图
第18题折线图
第18题扇形图
第18题折线图
第18题扇形图
第18题折线补全图
第18题扇形补全图
第23题表
第23题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
