人教版数学八年级上册15.1.1从分数到分式课件(共25张ppt)
文档属性
| 名称 | 人教版数学八年级上册15.1.1从分数到分式课件(共25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 352.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览








文档简介
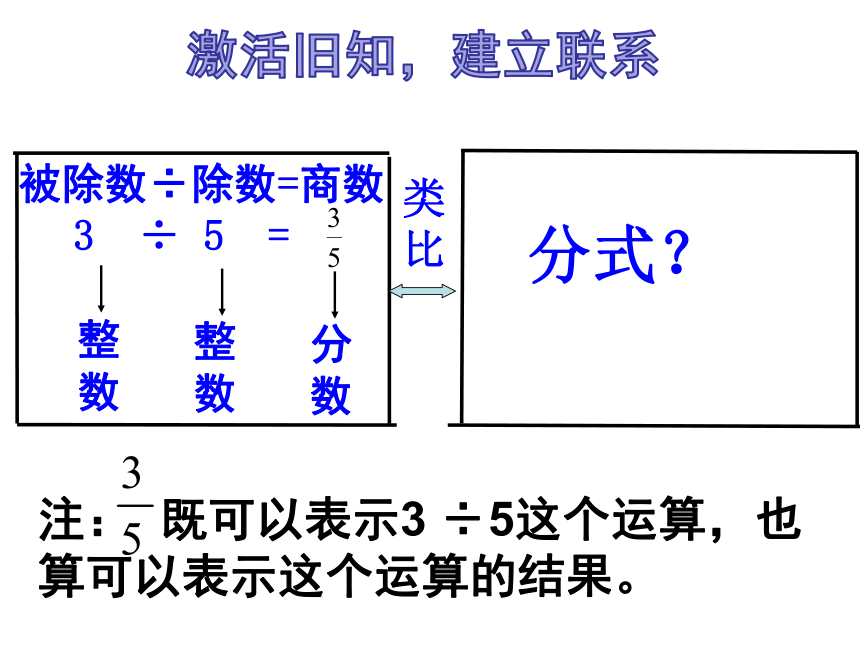
(共25张PPT)
分数
分式
类比
数学思想与方法回顾
15.1.1
从分数到分式
南宁市天桃实验学校
莫莉薇
整数
整数
分数
类比
分式?
3
÷
5
=
被除数÷除数=商数
注:
既可以表示3
÷5这个运算,也算可以表示这个运算的结果。
激活旧知,建立联系
填空:
(1)长方形的面积为10
cm
2,
长为7
cm,宽应为(
)cm
;
长方形的面积为S,长为
a
,
宽应为(
)
激活旧知,建立联系
(2)
把体积为200cm
3
的水倒入底面积为33cm
2圆柱形容器中,水面高度为(
)cm;把体积为V的水倒入底面积为S的圆柱形容器中,水面高度为(
)
(3)甲乙两人合作一项工程
a 天完成,则甲乙两人合作平均每天完成(
)
(4)轮船在静水中每小时走a千米/时,
水流速度为每小时 b 千米/
时,
轮船在顺水中航行
100 千米所用
的时间为( )小时;
轮船在逆水中航行 100 千米
所用的时间为( )小时
上面的问题中出现了以下式子:
活动一
新知探索
(1)它们与分数在表达形式中有什么相同点和不同点?
(2)它们和整式有什么样的区别?
(3)结合前面的例子,你认为分数和分式有什么联系?
填空:
(1)长方形的面积为10
cm
2,
长为7
cm,宽应为(
)cm
;
长方形的面积为S,长为
a
,
宽应为(
)
激活旧知,建立联系
类比分数、分式的表达形式:
整数
(A)
整数
(B)
分数
整式
(A)
整式(B)
分式(
)
A
B
a
类比
S
÷
a
=
S
7
÷
10
=
被除数÷除数=商数
被除式÷除式=商式
(
)
A
B
分数、分式之间的关系:
具体抽象化
分式与整式的不同:
分式的分母
中含有字母
分数
分式
特殊
一般
分式的定义:
整式
A
除以整式
B,可以表示
为
的形式。如果
含
有
,
那么称
为
。
其中
A
称为分式的分子,
B
称为分式的分母。
分母B
字母
分式
1
、
判断下列各式那些是分式?
√
√
√
√
判断一个式子是否是分式,不能把原式变形再判断,只能根据原来的形式判断。
注:数以结果论,式以形式论。
是
例题
要点归纳
1.判断一个式子是否是分式,不能把原式变形再判断,只能根据原来的形式判断。
注:数以结果论,式以形式论。
例:
不是分数,是整数,
而
是分式.
2.
是一个常数,故
为整式
3.
分母中一定含有字母。
判断下列各式哪些是整式,哪些是分式?
9x+4
【跟踪训练】
y3
y
y2-1
y-1
√
√
√
√
√
y3
π
做一做
3
、列式表示下列各量
(1)某村有n个人,耕地40公顷,人均耕地面积为(
)公顷。
(2)△ABC的面积为S,BC的边长为a,
高AD为(
)
(3)一辆汽车行驶a千米用
b
小时,它的平
均速度为(
)
千米/时,一列火车行驶a千米比
这辆汽车少用
1
小时它的平均
速度为(
)千米/时。
什么情况下分式
有意义?
什么情况下分式
无意义?
什么情况下分式
值为零?
小组讨论
活动二
要点归纳
分母
有意义
分母
无意义
分母
分母
值为0
练一练:
填空
1)当x
时,分式
有意义;
2)当x
时,分式
有意义;
3)当b
时,分式
有意义;
4)当x、y
满足关系
时,
分式
有意义;
≠0
≠1
≠
x≠y
练一练:
填空
1)当x
时,分式
的值等于0;
2)当x、y
满足关系
时,
分式
的值等于0
;
3)当x
时,分式
的值等于0;
=
0
x
=
-y
=1
且x
≠
y
活动三
小组讨论
你能列出一些分式,使分母中的字母不论取何值,这个分式都有意义吗?
请同学们谈谈通过本节课的学习活动,你学到那些知识和方法?或者你感受最深的是什么?
课堂小结:
分式的定义:
整式
A
除以整式
B,可以表示
为
的形式。如果
含
有
,
那么称
为
。
其中
A
称为分式的分子,
B
称为分式的分母。
分母B
字母
分式
要点归纳
1.判断一个式子是否是分式,不能把原式变形再判断,只能根据原来的形式判断。
注:数以结果论,式以形式论。
2.
是一个常数,故
为整式
3.
分母中一定含有字母。
过程与思想方法归纳
分数
分式
类比
迁移思想
旧知识
新知识
一致性
数式通性
分式的性质
分式的运算
分数
分式
类比
数学思想与方法回顾
15.1.1
从分数到分式
南宁市天桃实验学校
莫莉薇
整数
整数
分数
类比
分式?
3
÷
5
=
被除数÷除数=商数
注:
既可以表示3
÷5这个运算,也算可以表示这个运算的结果。
激活旧知,建立联系
填空:
(1)长方形的面积为10
cm
2,
长为7
cm,宽应为(
)cm
;
长方形的面积为S,长为
a
,
宽应为(
)
激活旧知,建立联系
(2)
把体积为200cm
3
的水倒入底面积为33cm
2圆柱形容器中,水面高度为(
)cm;把体积为V的水倒入底面积为S的圆柱形容器中,水面高度为(
)
(3)甲乙两人合作一项工程
a 天完成,则甲乙两人合作平均每天完成(
)
(4)轮船在静水中每小时走a千米/时,
水流速度为每小时 b 千米/
时,
轮船在顺水中航行
100 千米所用
的时间为( )小时;
轮船在逆水中航行 100 千米
所用的时间为( )小时
上面的问题中出现了以下式子:
活动一
新知探索
(1)它们与分数在表达形式中有什么相同点和不同点?
(2)它们和整式有什么样的区别?
(3)结合前面的例子,你认为分数和分式有什么联系?
填空:
(1)长方形的面积为10
cm
2,
长为7
cm,宽应为(
)cm
;
长方形的面积为S,长为
a
,
宽应为(
)
激活旧知,建立联系
类比分数、分式的表达形式:
整数
(A)
整数
(B)
分数
整式
(A)
整式(B)
分式(
)
A
B
a
类比
S
÷
a
=
S
7
÷
10
=
被除数÷除数=商数
被除式÷除式=商式
(
)
A
B
分数、分式之间的关系:
具体抽象化
分式与整式的不同:
分式的分母
中含有字母
分数
分式
特殊
一般
分式的定义:
整式
A
除以整式
B,可以表示
为
的形式。如果
含
有
,
那么称
为
。
其中
A
称为分式的分子,
B
称为分式的分母。
分母B
字母
分式
1
、
判断下列各式那些是分式?
√
√
√
√
判断一个式子是否是分式,不能把原式变形再判断,只能根据原来的形式判断。
注:数以结果论,式以形式论。
是
例题
要点归纳
1.判断一个式子是否是分式,不能把原式变形再判断,只能根据原来的形式判断。
注:数以结果论,式以形式论。
例:
不是分数,是整数,
而
是分式.
2.
是一个常数,故
为整式
3.
分母中一定含有字母。
判断下列各式哪些是整式,哪些是分式?
9x+4
【跟踪训练】
y3
y
y2-1
y-1
√
√
√
√
√
y3
π
做一做
3
、列式表示下列各量
(1)某村有n个人,耕地40公顷,人均耕地面积为(
)公顷。
(2)△ABC的面积为S,BC的边长为a,
高AD为(
)
(3)一辆汽车行驶a千米用
b
小时,它的平
均速度为(
)
千米/时,一列火车行驶a千米比
这辆汽车少用
1
小时它的平均
速度为(
)千米/时。
什么情况下分式
有意义?
什么情况下分式
无意义?
什么情况下分式
值为零?
小组讨论
活动二
要点归纳
分母
有意义
分母
无意义
分母
分母
值为0
练一练:
填空
1)当x
时,分式
有意义;
2)当x
时,分式
有意义;
3)当b
时,分式
有意义;
4)当x、y
满足关系
时,
分式
有意义;
≠0
≠1
≠
x≠y
练一练:
填空
1)当x
时,分式
的值等于0;
2)当x、y
满足关系
时,
分式
的值等于0
;
3)当x
时,分式
的值等于0;
=
0
x
=
-y
=1
且x
≠
y
活动三
小组讨论
你能列出一些分式,使分母中的字母不论取何值,这个分式都有意义吗?
请同学们谈谈通过本节课的学习活动,你学到那些知识和方法?或者你感受最深的是什么?
课堂小结:
分式的定义:
整式
A
除以整式
B,可以表示
为
的形式。如果
含
有
,
那么称
为
。
其中
A
称为分式的分子,
B
称为分式的分母。
分母B
字母
分式
要点归纳
1.判断一个式子是否是分式,不能把原式变形再判断,只能根据原来的形式判断。
注:数以结果论,式以形式论。
2.
是一个常数,故
为整式
3.
分母中一定含有字母。
过程与思想方法归纳
分数
分式
类比
迁移思想
旧知识
新知识
一致性
数式通性
分式的性质
分式的运算
