人教版九年级数学上册第二十四章圆第7课时切线的判定和性质讲义(含答案)
文档属性
| 名称 | 人教版九年级数学上册第二十四章圆第7课时切线的判定和性质讲义(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 237.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 00:00:00 | ||
图片预览

文档简介
人 教 版 九 年 级 数 学 上 册 讲 义
第二十四章 圆
第7课时切线的判定和性质
教学目的
1.掌握圆的切线的判定方法和切线的性质;
2.运用切线的判定和性质解决问题
教学重点
1.掌握圆的切线的判定方法和切线的性质;
2.运用切线的判定和性质解决问题
教学内容
知识要点 1.切线的判定
定 理:经过半径的外端并且垂直于这条 半径 的直线是圆的切线.
方 法:(1)切线的定义:和圆只有一个公共点的直线是圆的切线;
(2)与圆心的距离等于半径的直线是圆的切线;
(3)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.切线的性质
定 理:圆的切线垂直于过切点的 半径 .
总 结:(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于过切点的半径;
(4)经过圆心且垂直于切线的直线必过切点;
(5)经过切点且垂直于切线的直线必过圆心.
对应练习
1.下列说法中,正确的是( )
A.与圆有公共点的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到直线的距离等于半径的直线是圆的切线
2.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.
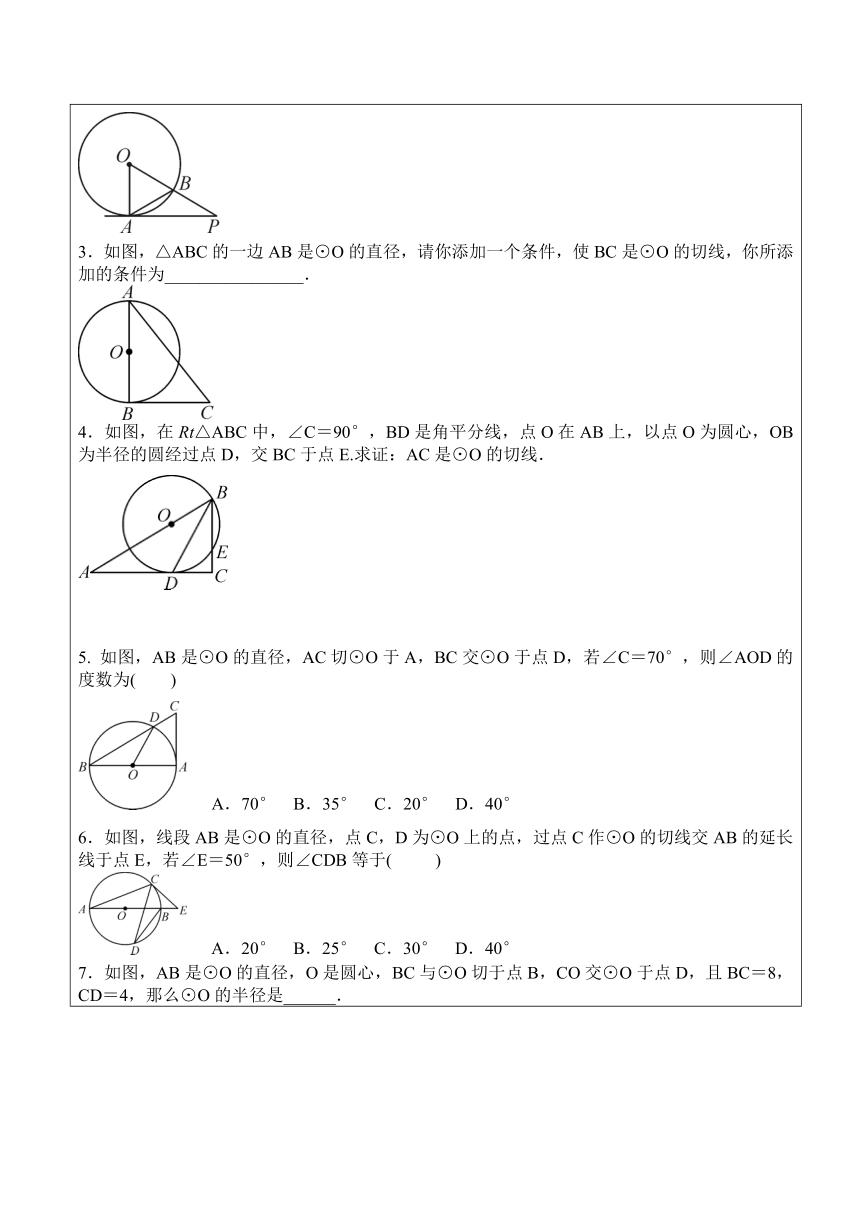
3.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.
4.如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.求证:AC是⊙O的切线.
5. 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70° B.35° C.20° D.40°
6.如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )
A.20° B.25° C.30° D.40°
7.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.
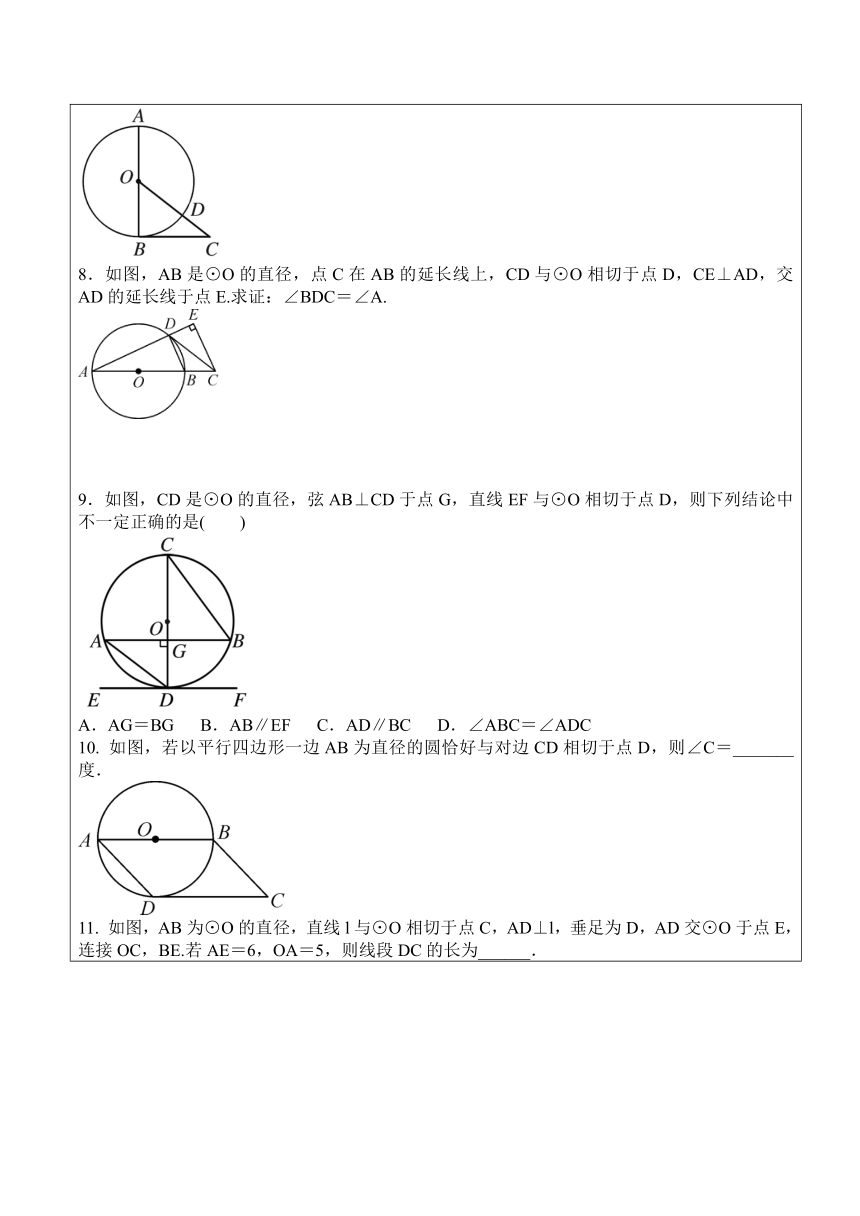
8.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.求证:∠BDC=∠A.
9.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
10. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.
11. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.
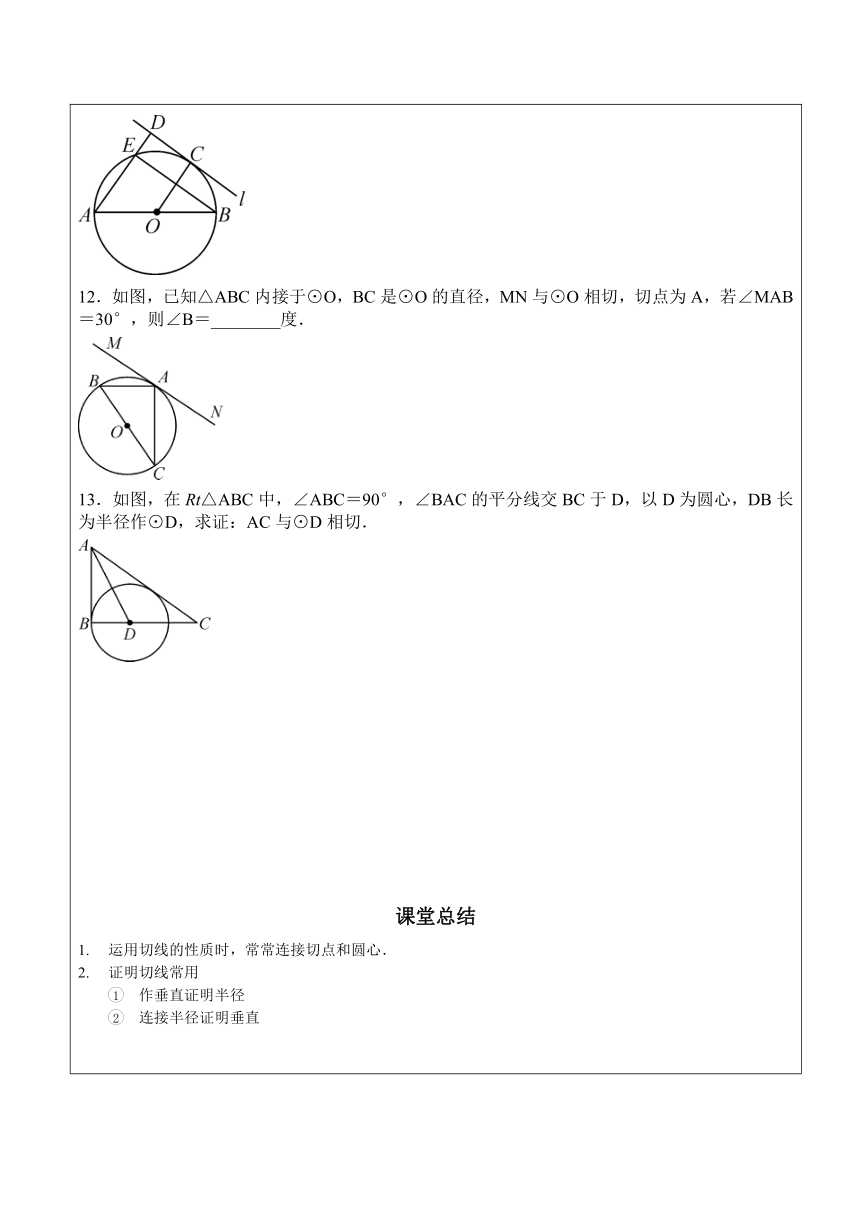
12.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=________度.
13.如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D,求证:AC与⊙D相切.
课堂总结
运用切线的性质时,常常连接切点和圆心.
证明切线常用
作垂直证明半径
连接半径证明垂直
课后练习
1.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为∠ABC= °.
2.下列说法中,正确的是( )
A.AB垂直于⊙O的半径,则AB是⊙O的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到直线的距离等于半径,那么这条直线是圆的切线
3.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.求证:CD是⊙O的切线.
4.如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则OB的长为( )
A.4 B.4
C.2 D.2
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
A.150° B.130°
C.155° D.135°
6.如图,PA切⊙O于A,PO交⊙O于B,若PA=6,PB=3,则⊙O的半径是( )
A.5 B.4
C.4.5 D.3.5
7.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A.若∠MAB=30°,则∠B= .
8.如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16.求OA的长.
9.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
A.20° B.25°
C.40° D.50°
10.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.30° B.45°
C.60° D.90°
如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°.给出下面四个结论:①AD=DC;②AB=BD;③AB=BC;④BD=CD.其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
12.如图,PA切⊙O于A,∠APO=20°,PO交⊙O于点B,C为圆上一点,则∠ACB= .
13.如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=2 cm,则切线AB= cm.
14.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切.
15.如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.求证:∠1=∠2.
16.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
练习答案 1. D
2. 相切
3. ∠ABC=90°
4. 解:连接OD,∵BD为∠ABC平分线,∴∠OBD=∠CBD,∵OB=OD,∴∠OBD=∠ODB,∴∠CBD=∠ODB,∴OD∥BC,∵∠C=90°,∴∠ODA=90°,则AC为⊙O的切线
5. D
6. A
7. 6
8. 解:连接OD,∵CD是⊙O的切线,∴∠ODC=90°,∴∠ODB+∠BDC=90°,∵AB是⊙O的直径,∴∠ADB=90°,即∠ODB+∠ADO=90°,∴∠BDC=∠ADO,∵OA=OD,∴∠ADO=∠A,∴∠BDC=∠A
9. C
10. 45
11. 4
12. 60
13. 解:过D作DH⊥AC于H,由角平分线的性质可证DB=DH,∴AC与⊙D相切
作业答案 1.90°.
2.D
3.
证明:连接OC.
∵AC=CD,∠D=30°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠OCA=∠A=30°.
∴∠COD=60°.
∴∠OCD=90°.
∴OC⊥CD.
∴CD是⊙O的切线.
4.B
5. B
6.C
7.60°.
8.
解:连接OC,
∵AB与⊙O相切于点C,
∴OC⊥AB.
∵∠A=∠B,∴OA=OB.
∴AC=BC=AB=8.
∵OC=6,
∴OA==10.
9.D
10.A
11.B
12.35°.
13.2cm.
14.证明:过点O作OD⊥PB于点D,连接OC.
∵PA切⊙O于点C,
∴OC⊥PA.
又∵点O在∠APB的平分线上,
∴OC=OD.
∴PB与⊙O相切.
15.证明:连接OD, ∵DE为⊙O的切线,
∴OD⊥DE.
∴∠ODE=90°,
即∠2+∠ODC=90°.
∵OC=OD,
∴∠C=∠ODC.
∴∠2+∠C=90°.
而OC⊥OB,
∴∠C+∠3=90°.∴∠2=∠3.
∵∠1=∠3,∴∠1=∠2.
16.
解:(1)证明:∵AC为直径,
∴∠ADC=90°.
∴∠A+∠DCA=90°.
∵∠ACB=90°,
∴∠DCB+∠ACD=90°.
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
连接DO,∵DO=CO,∴∠ODC=∠OCD.
∵DM=CM,∴∠MCD=∠MDC.
∵∠DCO+∠MCD=90°,
∴∠ODC+∠MDC=90°.
∴直线DM与⊙O相切.
第二十四章 圆
第7课时切线的判定和性质
教学目的
1.掌握圆的切线的判定方法和切线的性质;
2.运用切线的判定和性质解决问题
教学重点
1.掌握圆的切线的判定方法和切线的性质;
2.运用切线的判定和性质解决问题
教学内容
知识要点 1.切线的判定
定 理:经过半径的外端并且垂直于这条 半径 的直线是圆的切线.
方 法:(1)切线的定义:和圆只有一个公共点的直线是圆的切线;
(2)与圆心的距离等于半径的直线是圆的切线;
(3)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.切线的性质
定 理:圆的切线垂直于过切点的 半径 .
总 结:(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于过切点的半径;
(4)经过圆心且垂直于切线的直线必过切点;
(5)经过切点且垂直于切线的直线必过圆心.
对应练习
1.下列说法中,正确的是( )
A.与圆有公共点的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到直线的距离等于半径的直线是圆的切线
2.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.
3.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.
4.如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.求证:AC是⊙O的切线.
5. 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70° B.35° C.20° D.40°
6.如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )
A.20° B.25° C.30° D.40°
7.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.
8.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.求证:∠BDC=∠A.
9.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
10. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.
11. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.
12.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=________度.
13.如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D,求证:AC与⊙D相切.
课堂总结
运用切线的性质时,常常连接切点和圆心.
证明切线常用
作垂直证明半径
连接半径证明垂直
课后练习
1.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为∠ABC= °.
2.下列说法中,正确的是( )
A.AB垂直于⊙O的半径,则AB是⊙O的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到直线的距离等于半径,那么这条直线是圆的切线
3.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.求证:CD是⊙O的切线.
4.如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则OB的长为( )
A.4 B.4
C.2 D.2
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
A.150° B.130°
C.155° D.135°
6.如图,PA切⊙O于A,PO交⊙O于B,若PA=6,PB=3,则⊙O的半径是( )
A.5 B.4
C.4.5 D.3.5
7.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A.若∠MAB=30°,则∠B= .
8.如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16.求OA的长.
9.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
A.20° B.25°
C.40° D.50°
10.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.30° B.45°
C.60° D.90°
如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°.给出下面四个结论:①AD=DC;②AB=BD;③AB=BC;④BD=CD.其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
12.如图,PA切⊙O于A,∠APO=20°,PO交⊙O于点B,C为圆上一点,则∠ACB= .
13.如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=2 cm,则切线AB= cm.
14.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切.
15.如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.求证:∠1=∠2.
16.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
练习答案 1. D
2. 相切
3. ∠ABC=90°
4. 解:连接OD,∵BD为∠ABC平分线,∴∠OBD=∠CBD,∵OB=OD,∴∠OBD=∠ODB,∴∠CBD=∠ODB,∴OD∥BC,∵∠C=90°,∴∠ODA=90°,则AC为⊙O的切线
5. D
6. A
7. 6
8. 解:连接OD,∵CD是⊙O的切线,∴∠ODC=90°,∴∠ODB+∠BDC=90°,∵AB是⊙O的直径,∴∠ADB=90°,即∠ODB+∠ADO=90°,∴∠BDC=∠ADO,∵OA=OD,∴∠ADO=∠A,∴∠BDC=∠A
9. C
10. 45
11. 4
12. 60
13. 解:过D作DH⊥AC于H,由角平分线的性质可证DB=DH,∴AC与⊙D相切
作业答案 1.90°.
2.D
3.
证明:连接OC.
∵AC=CD,∠D=30°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠OCA=∠A=30°.
∴∠COD=60°.
∴∠OCD=90°.
∴OC⊥CD.
∴CD是⊙O的切线.
4.B
5. B
6.C
7.60°.
8.
解:连接OC,
∵AB与⊙O相切于点C,
∴OC⊥AB.
∵∠A=∠B,∴OA=OB.
∴AC=BC=AB=8.
∵OC=6,
∴OA==10.
9.D
10.A
11.B
12.35°.
13.2cm.
14.证明:过点O作OD⊥PB于点D,连接OC.
∵PA切⊙O于点C,
∴OC⊥PA.
又∵点O在∠APB的平分线上,
∴OC=OD.
∴PB与⊙O相切.
15.证明:连接OD, ∵DE为⊙O的切线,
∴OD⊥DE.
∴∠ODE=90°,
即∠2+∠ODC=90°.
∵OC=OD,
∴∠C=∠ODC.
∴∠2+∠C=90°.
而OC⊥OB,
∴∠C+∠3=90°.∴∠2=∠3.
∵∠1=∠3,∴∠1=∠2.
16.
解:(1)证明:∵AC为直径,
∴∠ADC=90°.
∴∠A+∠DCA=90°.
∵∠ACB=90°,
∴∠DCB+∠ACD=90°.
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
连接DO,∵DO=CO,∴∠ODC=∠OCD.
∵DM=CM,∴∠MCD=∠MDC.
∵∠DCO+∠MCD=90°,
∴∠ODC+∠MDC=90°.
∴直线DM与⊙O相切.
同课章节目录
