第24章圆第9课时正多边形和圆-人教版九年级数学上册讲义(机构专用)(word含答案)
文档属性
| 名称 | 第24章圆第9课时正多边形和圆-人教版九年级数学上册讲义(机构专用)(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 662.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:31:26 | ||
图片预览



文档简介
人 教 版 九 年 级 数 学 上 册 讲 义
第二十四章 圆
正多边形和圆
教学目的
了解正多边形的有关概念和圆内正多边形
教学重点
解决圆内正多边形的有关的问题
教学内容
知识要点 1.正多边形
定 义:各 边 相等、各 角 也相等的多边形叫做正多边形.
2.正多边形与圆的关系
规 律:把圆分成n(n≥3)等份,依次连接各分点所得的多边形是圆的内接正n边形.
3.正多边形的有关概念
中 心:正多边形的外接圆(或内切圆)的 圆心 叫做正多边形的中心.
半 径:正多边形的 外接圆 的半径叫做正多边形的半径.
中心角:正多边形每一边所对的 圆心角 叫做正多边形的中心角.
边心距:正多边形的中心到正多边形的一边的 距离 叫做正多边形的边心距.
对应练习
1. 如图 ,正方形ABCD内接于⊙O,AB=4,则图中阴影部分的面积是( )
A.4π-16 B.8π-16
C.16π-32 D.32π-16
2.在正三角形、正五边形、正十边形和正十五边形中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个
C.3个 D.4个
3.一个正n边形的中心角是它的一个内角的,则n的值为( )
A.12 B.11
C.10 D.8
4.如图 所示,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长
B.弦AC的长等于圆内接正十二边形的边长
C.=
D.∠BAC=30°
5.如图 ,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB的度数为( )
A.30° B.35° C.40° D.60°
6.正六边形的边心距与边长之比为( )
A.∶3 B.∶2 C.1∶2 D.∶2
7.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是( )
A.36° B.60° C.72° D.108°
8.若正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为( )
A.正十二边形 B.正六边形
C.正方形 D.正三角形
9.如图所示,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ的度数为( )
A.60° B.65° C.72° D.75°
10.已知正六边形的边长为a,则它的内切圆的面积为________.
11.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为________.
12.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.若AE恰好为⊙O的内接正十边形的一边,∠DAE的度数为________.
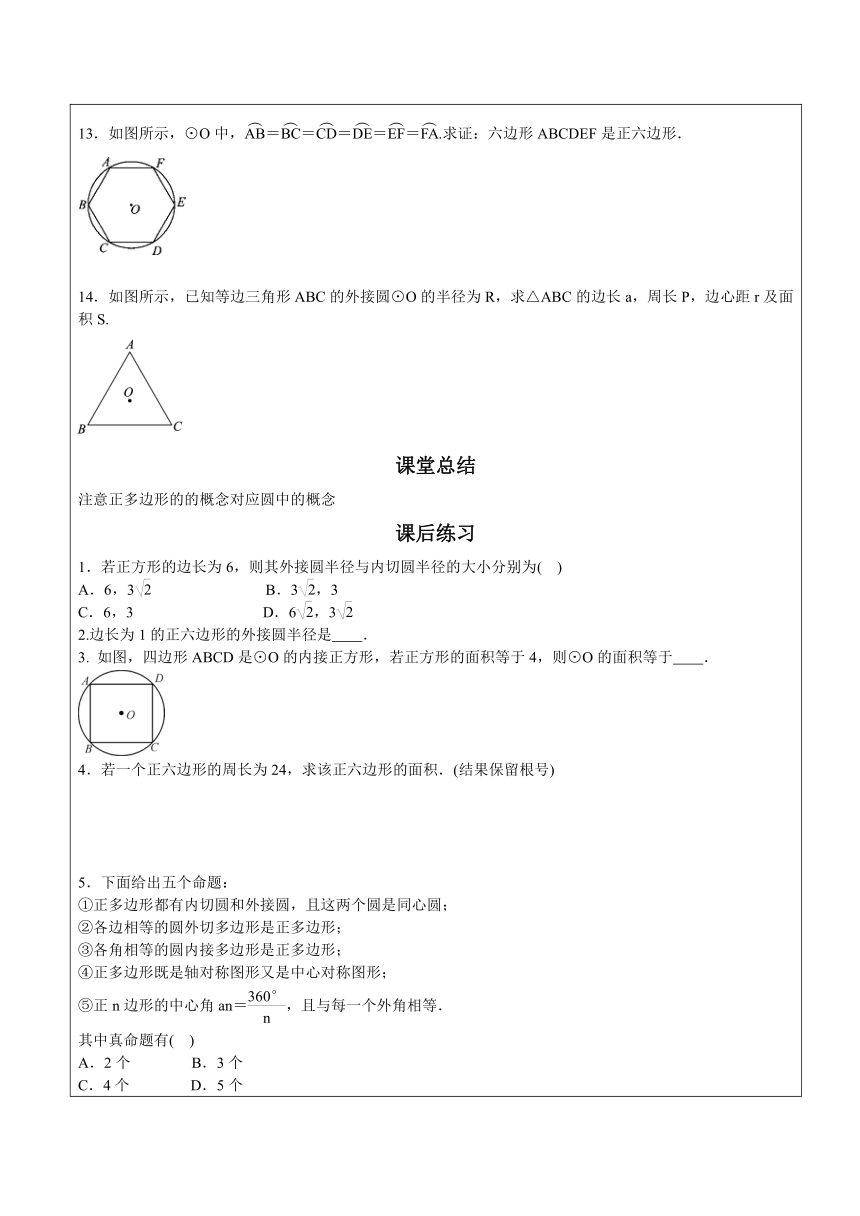
13.如图所示,⊙O中,=====.求证:六边形ABCDEF是正六边形.
14.如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a,周长P,边心距r及面积S.
课堂总结
注意正多边形的的概念对应圆中的概念
课后练习
1.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.3,3
C.6,3 D.6,3
2.边长为1的正六边形的外接圆半径是 .
3. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
4.若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
5.下面给出五个命题:
①正多边形都有内切圆和外接圆,且这两个圆是同心圆;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④正多边形既是轴对称图形又是中心对称图形;
⑤正n边形的中心角an=,且与每一个外角相等.
其中真命题有( )
A.2个 B.3个
C.4个 D.5个
6.正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r
C.2R=3r D.R=2r
7.正六边形的边心距为,则该正六边形的边长是( )
A. B.2
C.3 D.2
8.如图,正六边形ABCDEF的边长为2,则对角线AE的长是 .
9.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
10.如图所示,正五边形ABCDE的对角线AC和BE相交于点M.求证:
(1)AC∥DE;
(2)ME=AE.
练习答案 1.
[解析] B 连结OA,OB,如图.
∵四边形ABCD为正方形,∴∠AOB=90°.设OA=OB=r,则r2+r2=42,解得r=2 .
∴S阴影=S⊙O-S正方形ABCD=π×(2 )2-42=8π-16.
故选B.
2.[答案] A
3.[答案] A
4.[解析] D 因为OA=OB=AB,所以△OAB是等边三角形.又因为OC⊥AB,所以∠AOC=∠BOC=30°,所以∠BAC=15°,=,所以A,B,C正确,D不正确.
5.[答案] A
6.[解析] B 如图,设正六边形的边长是a,则其半径长也是a.
过正六边形的中心O作边AB的垂线段OC,连结OA,OB,则AC=AB=a,
∴OC==a,
∴正六边形的边心距与边长之比为a∶a=∶2.故选B.
7.[答案] C
8.[解析] B 正多边形的内切圆与外接圆的周长之比为∶2,则半径之比为∶2.
如图,设AB是正多边形的一边,O为正多边形内切圆与外接圆的圆心,OC⊥AB于点C,OC=k,则OA=OB=2k,
在Rt△AOC中,
=,
∴∠AOC=30°,
∴∠AOB=60°,
则正多边形的边数是=6.故选B.
9.[解析] D 因为圆心角与它所对弧的度数相等,所以求出的度数就求出了∠AOQ的大小,而=-.根据题意,得所对的圆心角为120°,所对的圆心角为×360°=45°,所以 所对的圆心角为120°-45°=75°,所以∠AOQ=75°.
10.[答案]
11.[答案] 18
[解析] 由题意可得,正六边形的边长AB就是扇形的半径,正六边形的边长BC,CD,DE,EF的和就是扇形的弧长,所以扇形AFB的半径AB=3,弧BDF的长为12,
所以扇形AFB(阴影部分)的面积为S=rl=×3×12=18.故答案为18.
12.[答案] 42°
[解析] 连结BD,OA,OE,OD,如图所示.
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°.
∵∠C=120°,∴∠BAD=60°.
又∵AB=AD,∴△ABD是等边三角形,
∴∠ABD=60°,∴∠AOD=2∠ABD=120°.
∵AE恰好为⊙O的内接正十边形的一边,
∴∠AOE=360°÷10=36°,
∴∠DOE=120°-36°=84°,∴∠DAE=42°.
13.[解析] 由弧相等得到弦相等,从而证得该六边形的六条边相等,由弧相等也可以证得该六边形的六个内角相等.
证明:∵=====,
∴AB=BC=CD=DE=EF=FA(等弧所对的弦相等).
∵=====,
∴∠A=∠B=∠C=∠D=∠E=∠F(等弧所对的圆周角相等),
∴六边形ABCDEF是正六边形.
14.解:如图,连结OB,OC,过点O作OD⊥BC于点D,则OB=R,∠OBD=∠ABC=30°,∴OD=OB=R,
∴a=2·=2·R=R,
P=3a=3R,
r=OD=R,
S=3·ar=3××R×R=R2.
作业答案 1. B
2. 1.
3. 2π.
4.
解:如图,过点O作OD⊥AB,垂足为D.∵∠AOB=360°÷6=60°,OA=OB,∴△AOB为等边三角形,且三条对角线把正六边形分成了六个全等的等边三角形.
∵正六边形的周长为24,∴AB=4.
∵OD⊥AB,∴∠AOD=30°,AD=2.
在Rt△AOD中,根据勾股定理得OD=2.
∴S△AOB=×4×2=4.
∴S正六边形=6×4=24.
5. A
6.D
7.B
8. 2.
9.
解:(1)证明:∵五边形ABCDE是正五边形,
∴AB=BC,∠ABM=∠BCN.
在△ABM和△BCN中,
AB=BC,∠ABM=∠BCN,BM=CN,
∴△ABM≌△BCN(SAS).
(2)∵△ABM≌△BCN,
∴∠MBP=∠BAP.
∵∠MBP+∠BMP+∠BPM=180°,∠BAP+∠BMA+∠MBA=180°,
∴∠BPM=∠MBA.
∵∠BPM=∠APN,
∴∠APN=∠MBA===108°.
10.
证明:(1)由题意得∠EDC=×3×=108°,∠DCA=×2×=72°.
∴∠EDC+∠DCA=108°+72°=180°.
∴AC∥DE.
(2)由题意得
∠DEB=∠EAC=×2×=72°.
∵AC∥DE,∴∠AME=∠DEB=72°.
∴∠AME=∠EAC.∴ME=AE.
第二十四章 圆
正多边形和圆
教学目的
了解正多边形的有关概念和圆内正多边形
教学重点
解决圆内正多边形的有关的问题
教学内容
知识要点 1.正多边形
定 义:各 边 相等、各 角 也相等的多边形叫做正多边形.
2.正多边形与圆的关系
规 律:把圆分成n(n≥3)等份,依次连接各分点所得的多边形是圆的内接正n边形.
3.正多边形的有关概念
中 心:正多边形的外接圆(或内切圆)的 圆心 叫做正多边形的中心.
半 径:正多边形的 外接圆 的半径叫做正多边形的半径.
中心角:正多边形每一边所对的 圆心角 叫做正多边形的中心角.
边心距:正多边形的中心到正多边形的一边的 距离 叫做正多边形的边心距.
对应练习
1. 如图 ,正方形ABCD内接于⊙O,AB=4,则图中阴影部分的面积是( )
A.4π-16 B.8π-16
C.16π-32 D.32π-16
2.在正三角形、正五边形、正十边形和正十五边形中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个
C.3个 D.4个
3.一个正n边形的中心角是它的一个内角的,则n的值为( )
A.12 B.11
C.10 D.8
4.如图 所示,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长
B.弦AC的长等于圆内接正十二边形的边长
C.=
D.∠BAC=30°
5.如图 ,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB的度数为( )
A.30° B.35° C.40° D.60°
6.正六边形的边心距与边长之比为( )
A.∶3 B.∶2 C.1∶2 D.∶2
7.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是( )
A.36° B.60° C.72° D.108°
8.若正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为( )
A.正十二边形 B.正六边形
C.正方形 D.正三角形
9.如图所示,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ的度数为( )
A.60° B.65° C.72° D.75°
10.已知正六边形的边长为a,则它的内切圆的面积为________.
11.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为________.
12.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.若AE恰好为⊙O的内接正十边形的一边,∠DAE的度数为________.
13.如图所示,⊙O中,=====.求证:六边形ABCDEF是正六边形.
14.如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a,周长P,边心距r及面积S.
课堂总结
注意正多边形的的概念对应圆中的概念
课后练习
1.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.3,3
C.6,3 D.6,3
2.边长为1的正六边形的外接圆半径是 .
3. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
4.若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
5.下面给出五个命题:
①正多边形都有内切圆和外接圆,且这两个圆是同心圆;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④正多边形既是轴对称图形又是中心对称图形;
⑤正n边形的中心角an=,且与每一个外角相等.
其中真命题有( )
A.2个 B.3个
C.4个 D.5个
6.正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r
C.2R=3r D.R=2r
7.正六边形的边心距为,则该正六边形的边长是( )
A. B.2
C.3 D.2
8.如图,正六边形ABCDEF的边长为2,则对角线AE的长是 .
9.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
10.如图所示,正五边形ABCDE的对角线AC和BE相交于点M.求证:
(1)AC∥DE;
(2)ME=AE.
练习答案 1.
[解析] B 连结OA,OB,如图.
∵四边形ABCD为正方形,∴∠AOB=90°.设OA=OB=r,则r2+r2=42,解得r=2 .
∴S阴影=S⊙O-S正方形ABCD=π×(2 )2-42=8π-16.
故选B.
2.[答案] A
3.[答案] A
4.[解析] D 因为OA=OB=AB,所以△OAB是等边三角形.又因为OC⊥AB,所以∠AOC=∠BOC=30°,所以∠BAC=15°,=,所以A,B,C正确,D不正确.
5.[答案] A
6.[解析] B 如图,设正六边形的边长是a,则其半径长也是a.
过正六边形的中心O作边AB的垂线段OC,连结OA,OB,则AC=AB=a,
∴OC==a,
∴正六边形的边心距与边长之比为a∶a=∶2.故选B.
7.[答案] C
8.[解析] B 正多边形的内切圆与外接圆的周长之比为∶2,则半径之比为∶2.
如图,设AB是正多边形的一边,O为正多边形内切圆与外接圆的圆心,OC⊥AB于点C,OC=k,则OA=OB=2k,
在Rt△AOC中,
=,
∴∠AOC=30°,
∴∠AOB=60°,
则正多边形的边数是=6.故选B.
9.[解析] D 因为圆心角与它所对弧的度数相等,所以求出的度数就求出了∠AOQ的大小,而=-.根据题意,得所对的圆心角为120°,所对的圆心角为×360°=45°,所以 所对的圆心角为120°-45°=75°,所以∠AOQ=75°.
10.[答案]
11.[答案] 18
[解析] 由题意可得,正六边形的边长AB就是扇形的半径,正六边形的边长BC,CD,DE,EF的和就是扇形的弧长,所以扇形AFB的半径AB=3,弧BDF的长为12,
所以扇形AFB(阴影部分)的面积为S=rl=×3×12=18.故答案为18.
12.[答案] 42°
[解析] 连结BD,OA,OE,OD,如图所示.
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°.
∵∠C=120°,∴∠BAD=60°.
又∵AB=AD,∴△ABD是等边三角形,
∴∠ABD=60°,∴∠AOD=2∠ABD=120°.
∵AE恰好为⊙O的内接正十边形的一边,
∴∠AOE=360°÷10=36°,
∴∠DOE=120°-36°=84°,∴∠DAE=42°.
13.[解析] 由弧相等得到弦相等,从而证得该六边形的六条边相等,由弧相等也可以证得该六边形的六个内角相等.
证明:∵=====,
∴AB=BC=CD=DE=EF=FA(等弧所对的弦相等).
∵=====,
∴∠A=∠B=∠C=∠D=∠E=∠F(等弧所对的圆周角相等),
∴六边形ABCDEF是正六边形.
14.解:如图,连结OB,OC,过点O作OD⊥BC于点D,则OB=R,∠OBD=∠ABC=30°,∴OD=OB=R,
∴a=2·=2·R=R,
P=3a=3R,
r=OD=R,
S=3·ar=3××R×R=R2.
作业答案 1. B
2. 1.
3. 2π.
4.
解:如图,过点O作OD⊥AB,垂足为D.∵∠AOB=360°÷6=60°,OA=OB,∴△AOB为等边三角形,且三条对角线把正六边形分成了六个全等的等边三角形.
∵正六边形的周长为24,∴AB=4.
∵OD⊥AB,∴∠AOD=30°,AD=2.
在Rt△AOD中,根据勾股定理得OD=2.
∴S△AOB=×4×2=4.
∴S正六边形=6×4=24.
5. A
6.D
7.B
8. 2.
9.
解:(1)证明:∵五边形ABCDE是正五边形,
∴AB=BC,∠ABM=∠BCN.
在△ABM和△BCN中,
AB=BC,∠ABM=∠BCN,BM=CN,
∴△ABM≌△BCN(SAS).
(2)∵△ABM≌△BCN,
∴∠MBP=∠BAP.
∵∠MBP+∠BMP+∠BPM=180°,∠BAP+∠BMA+∠MBA=180°,
∴∠BPM=∠MBA.
∵∠BPM=∠APN,
∴∠APN=∠MBA===108°.
10.
证明:(1)由题意得∠EDC=×3×=108°,∠DCA=×2×=72°.
∴∠EDC+∠DCA=108°+72°=180°.
∴AC∥DE.
(2)由题意得
∠DEB=∠EAC=×2×=72°.
∵AC∥DE,∴∠AME=∠DEB=72°.
∴∠AME=∠EAC.∴ME=AE.
同课章节目录
