第24章圆第8课时 切线长定理和三角形的内切圆-人教版九年级数学上册讲义(机构专用)(word含答案)
文档属性
| 名称 | 第24章圆第8课时 切线长定理和三角形的内切圆-人教版九年级数学上册讲义(机构专用)(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览

文档简介
人 教 版 九 年 级 数 学 上 册 讲 义
第二十四章 圆
第8课时 切线长定理和三角形的内切圆
教学目的
1.掌握切线长的定义及其定理,并利用定理进行有关的计算;
2.了解三角形的内切圆、内心的概念,会作三角形的内切圆.
教学重点
掌握切线长的定义及其定理,并利用定理进行有关的计算
教学内容
知识要点 1.切线长
定 义:经过圆外的圆的切线上,这点和切点之间 线段的长 ,叫做这点到圆的切线长.
定 理:从圆外一点可以引圆的两条切线,它们的切线长 相等 ,这一点和圆心的连线平分两条切线的 夹角 .
2.三角形的内切圆、内心的概念
三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心叫做三角形的内心,它是三角形三条 角平分线 的交点.
对应练习
1.下列说法中,不正确的是( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.给出下列说法:
①任意一个三角形一定有一个外接圆,并且只有一个外接圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个内切圆,并且只有一个内切圆;
④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中正确的有( )
A.1个 B.2个[
C.3个 D.4个
3.如图,⊙I是△ABC的内切圆,切点分别为点D.E.F,若∠DEF=52o,
则∠A的度为________.
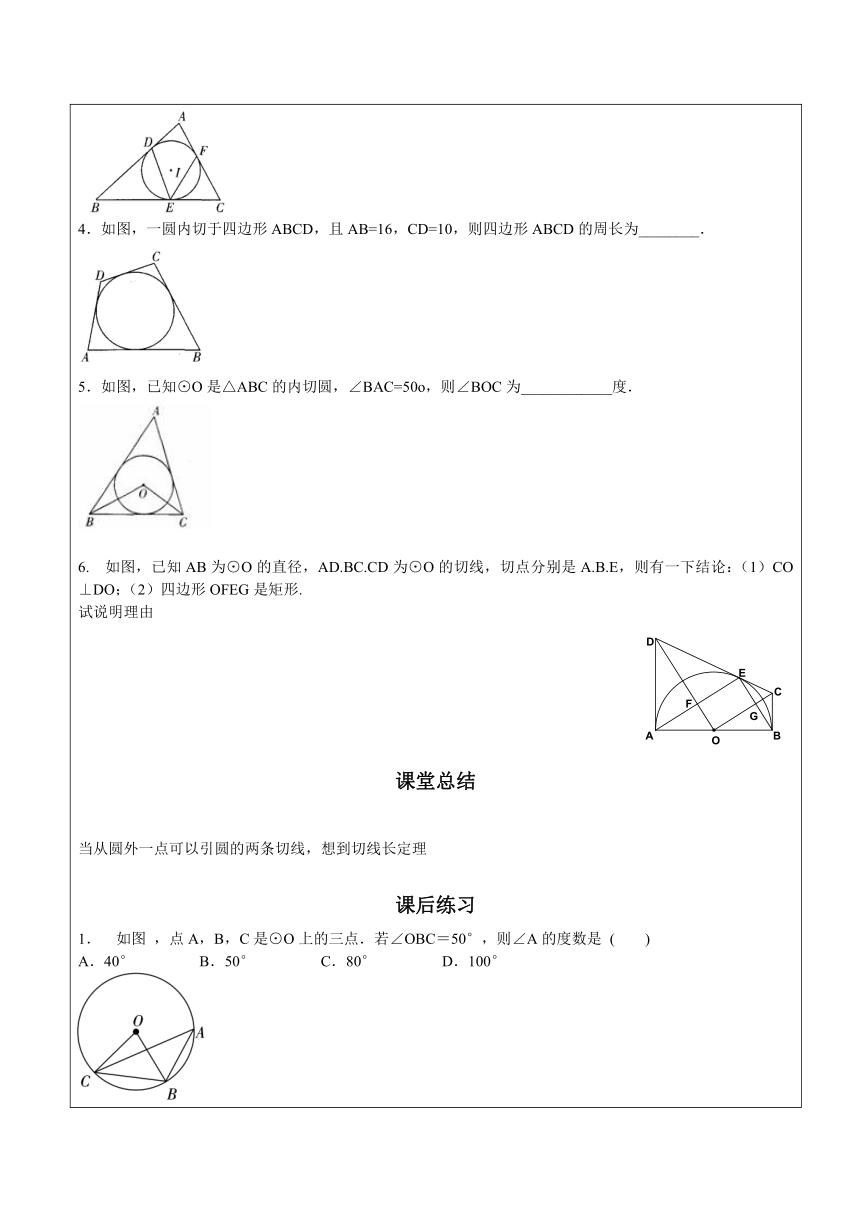
4.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
5.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
6. 如图,已知AB为⊙O的直径,AD.BC.CD为⊙O的切线,切点分别是A.B.E,则有一下结论:(1)CO⊥DO;(2)四边形OFEG是矩形.
试说明理由
课堂总结
当从圆外一点可以引圆的两条切线,想到切线长定理
课后练习
如图 ,点A,B,C是⊙O上的三点.若∠OBC=50°,则∠A的度数是 ( )
A.40° B.50° C.80° D.100°
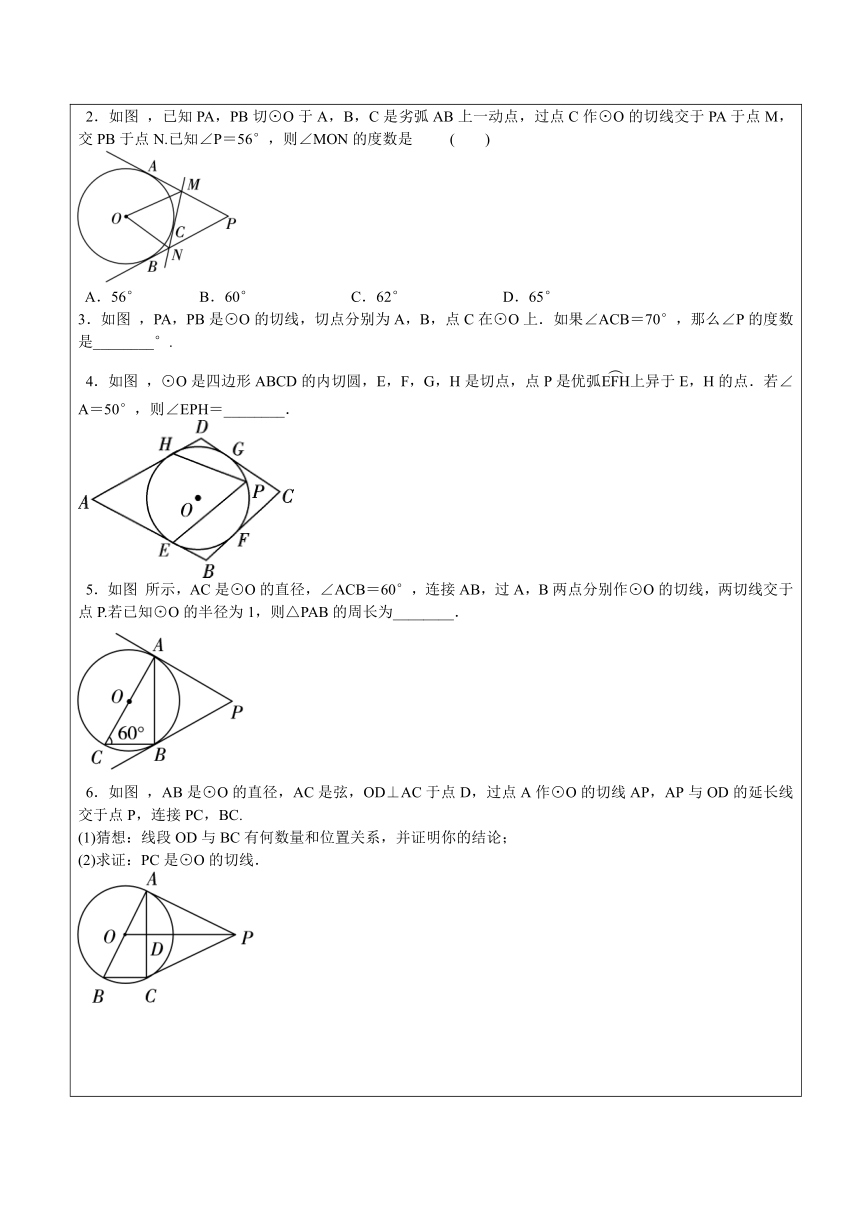
2.如图 ,已知PA,PB切⊙O于A,B,C是劣弧AB上一动点,过点C作⊙O的切线交于PA于点M,交PB于点N.已知∠P=56°,则∠MON的度数是 ( )
A.56° B.60° C.62° D.65°
3.如图 ,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上.如果∠ACB=70°,那么∠P的度数是________°.
4.如图 ,⊙O是四边形ABCD的内切圆,E,F,G,H是切点,点P是优弧上异于E,H的点.若∠A=50°,则∠EPH=________.
5.如图 所示,AC是⊙O的直径,∠ACB=60°,连接AB,过A,B两点分别作⊙O的切线,两切线交于点P.若已知⊙O的半径为1,则△PAB的周长为________.
6.如图 ,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC,BC.
(1)猜想:线段OD与BC有何数量和位置关系,并证明你的结论;
(2)求证:PC是⊙O的切线.
7.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长(结果保留根号).
9.
练习答案 1. C
2. B (提示:②④错误)
3. 76°
(提示:连接ID,IF
∵∠DEF=52°
∴∠DIF=104°
∵D.F是切点
∴DI⊥AB,IF⊥AC
∴∠ADI=∠AFI=90°
∴∠A=1800-1040=76°)
4. 52 (提示:AB+CD=AD+BC)
5. 115°(提示:∵∠A=50°
∴∠ABC+∠ACB=130°
∵OB,OC分别平分∠ABC,∠ACB
∴∠OBC+∠OCB=65°
∴∠BOC=180°-65°=115°
作业答案
1.A 2.C 3.40 4.65° 5.3
6.
7.
8.
9.
第二十四章 圆
第8课时 切线长定理和三角形的内切圆
教学目的
1.掌握切线长的定义及其定理,并利用定理进行有关的计算;
2.了解三角形的内切圆、内心的概念,会作三角形的内切圆.
教学重点
掌握切线长的定义及其定理,并利用定理进行有关的计算
教学内容
知识要点 1.切线长
定 义:经过圆外的圆的切线上,这点和切点之间 线段的长 ,叫做这点到圆的切线长.
定 理:从圆外一点可以引圆的两条切线,它们的切线长 相等 ,这一点和圆心的连线平分两条切线的 夹角 .
2.三角形的内切圆、内心的概念
三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心叫做三角形的内心,它是三角形三条 角平分线 的交点.
对应练习
1.下列说法中,不正确的是( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.给出下列说法:
①任意一个三角形一定有一个外接圆,并且只有一个外接圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个内切圆,并且只有一个内切圆;
④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中正确的有( )
A.1个 B.2个[
C.3个 D.4个
3.如图,⊙I是△ABC的内切圆,切点分别为点D.E.F,若∠DEF=52o,
则∠A的度为________.
4.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
5.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
6. 如图,已知AB为⊙O的直径,AD.BC.CD为⊙O的切线,切点分别是A.B.E,则有一下结论:(1)CO⊥DO;(2)四边形OFEG是矩形.
试说明理由
课堂总结
当从圆外一点可以引圆的两条切线,想到切线长定理
课后练习
如图 ,点A,B,C是⊙O上的三点.若∠OBC=50°,则∠A的度数是 ( )
A.40° B.50° C.80° D.100°
2.如图 ,已知PA,PB切⊙O于A,B,C是劣弧AB上一动点,过点C作⊙O的切线交于PA于点M,交PB于点N.已知∠P=56°,则∠MON的度数是 ( )
A.56° B.60° C.62° D.65°
3.如图 ,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上.如果∠ACB=70°,那么∠P的度数是________°.
4.如图 ,⊙O是四边形ABCD的内切圆,E,F,G,H是切点,点P是优弧上异于E,H的点.若∠A=50°,则∠EPH=________.
5.如图 所示,AC是⊙O的直径,∠ACB=60°,连接AB,过A,B两点分别作⊙O的切线,两切线交于点P.若已知⊙O的半径为1,则△PAB的周长为________.
6.如图 ,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC,BC.
(1)猜想:线段OD与BC有何数量和位置关系,并证明你的结论;
(2)求证:PC是⊙O的切线.
7.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长(结果保留根号).
9.
练习答案 1. C
2. B (提示:②④错误)
3. 76°
(提示:连接ID,IF
∵∠DEF=52°
∴∠DIF=104°
∵D.F是切点
∴DI⊥AB,IF⊥AC
∴∠ADI=∠AFI=90°
∴∠A=1800-1040=76°)
4. 52 (提示:AB+CD=AD+BC)
5. 115°(提示:∵∠A=50°
∴∠ABC+∠ACB=130°
∵OB,OC分别平分∠ABC,∠ACB
∴∠OBC+∠OCB=65°
∴∠BOC=180°-65°=115°
作业答案
1.A 2.C 3.40 4.65° 5.3
6.
7.
8.
9.
同课章节目录
