人教版数学九年级下册27.2.1探究判定三角形相似的第一定理教案
文档属性
| 名称 | 人教版数学九年级下册27.2.1探究判定三角形相似的第一定理教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 53.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-20 21:12:20 | ||
图片预览

文档简介
27.2.1
相似三角形的判定
第1课时
平行线法
教学目标
知识技能:
了解相似三角形的概念,掌握“平行线分线段成比例”的基本事实,经历“平行线判定三角形相似”的证明过程,掌握平行线判定三角形相似的方法,并在此基础上利用三角形的性质解决边和角的计算问题.
数学思想与问题解决
1.从图形全等到图形相似,初步感知全等是相似的特殊情况,相似三角形是全等三角形的拓展与发展.
2.正探究平行线判定三角形相似的过程中,经历利用平行线分线段成比例基本事实转化在三角形转化,提炼数学的划归思想.
3.能根据平行线分线段判定相似三角形,能利用相似三角形性质解决边和角的计算问题.
情感态度
通过观察、测量、抽象平行线分线段成比例定理,培养学生动手能力和直觉思维,在探究平行线判定相似的证明过程中,培养学生合情推理的能力及他们合作交流,积极探索与实践的良好习惯.
重点难点
重点:掌握平行线分线段成比例的基本事实,利用平行线判定相似三角形,能利用相似三角形性质解决边和角的计算问题.
难点:探究平行线判定相似三角形的方法.
教学设计
一、回顾旧知,
1.什么叫做相似图形?
2.什么叫做比例线段?比例有哪些性质?
3.相似多边形要满足哪些条件?相似多边形有哪些性质?
阅读课本
感受新知
1.对应角_________,对应边的比_________的两个三角形相似.如果△ABC~△,且△ABC与的相似比为k,则与△ABC的相似比为_______________.
2.平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段_______.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段______.
3.平行于三角形一边的直线与其他两边相交,所构成的三角形与原的三角形______.
三、探究新知
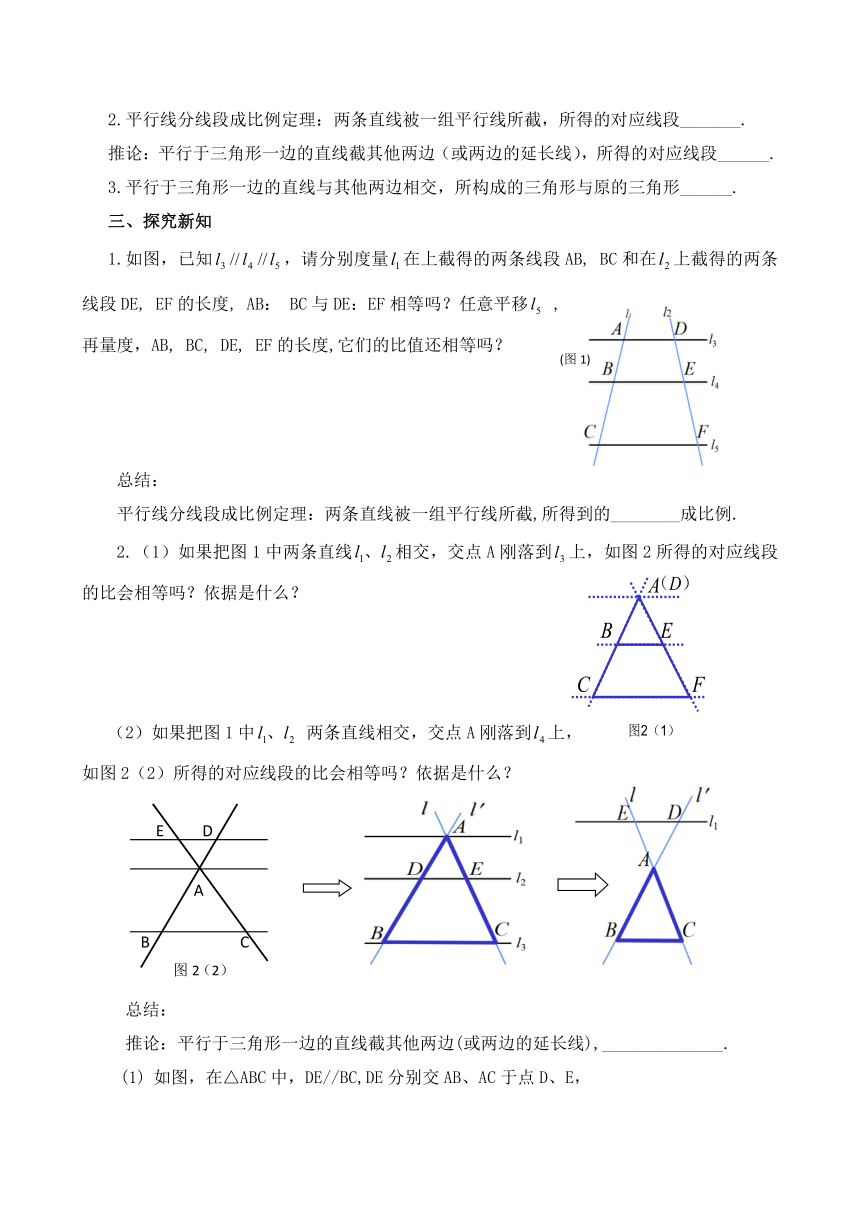
1.如图,已知,请分别度量在上截得的两条线段AB,
BC和在上截得的两条线段DE,
EF的长度,
AB:
BC与DE:EF相等吗?任意平移
,
(
(
图
1
)
)再量度,AB,
BC,
DE,
EF的长度,它们的比值还相等吗?
总结:
平行线分线段成比例定理:两条直线被一组平行线所截,所得到的________成比例.
2.(1)如果把图1中两条直线相交,交点A刚落到上,如图2所得的对应线段的比会相等吗?依据是什么?
(2)如果把图1中
两条直线相交,交点A刚落到上,
如图2(2)所得的对应线段的比会相等吗?依据是什么?
(
E
C
B
A
D
图
2
(
2
)
)
总结:
推论:平行于三角形一边的直线截其他两边(或两边的延长线),______________.
如图,在△ABC中,DE//BC,DE分别交AB、AC于点D、E,
(
A
D
E
B
C
)你能证明△ADE∽△ABC吗?
(
A
D
E
B
C
)(2)
如图,在△ABC中,DE//BC,DE分别交BA、CA的延长线于点D、E,
你能证明△ADE∽△ABC吗?
总结:平行于三角形一边的直线和其他两边(或两边的________)相交,所构成的三角形与原三角形相似.
四、应用新知
例:1
如图,在△ABC中,DE∥BC,AC=4
,AB=3,EC=1.
求AD和BD.
(
A
C
F
B
D
E
c
a
b
)练习:1.
如图,直线a//b//c,另两条直线分别交a、b、c
于点A、B、C及点D、E、F,且AB=3,DE=4,EF=2,则(
)
BC:DE=1:2
B.
BC:DE=2:3
C.
BC·DE=8
D.
BC·DE=6
2.如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论中正确的是(
)
A.
B.
C.
D.
(
mm
A
C
F
B
D
E
c
a
b
n
第
3
题
)3.如图,已知直线a//b//c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=________.
(
A
B
C
D
E
F
第
2
题
)
4.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
五、归纳小结,布置作业
课堂小结:1.平行线分线段成比例的基本事实是什么?推论是?
2.目前我们有什么方法判定两个三角形相似?
3.本课两个重要结论在探究中主要运用了哪些数学思想方法?
教学反思:
相似三角形的判定
第1课时
平行线法
教学目标
知识技能:
了解相似三角形的概念,掌握“平行线分线段成比例”的基本事实,经历“平行线判定三角形相似”的证明过程,掌握平行线判定三角形相似的方法,并在此基础上利用三角形的性质解决边和角的计算问题.
数学思想与问题解决
1.从图形全等到图形相似,初步感知全等是相似的特殊情况,相似三角形是全等三角形的拓展与发展.
2.正探究平行线判定三角形相似的过程中,经历利用平行线分线段成比例基本事实转化在三角形转化,提炼数学的划归思想.
3.能根据平行线分线段判定相似三角形,能利用相似三角形性质解决边和角的计算问题.
情感态度
通过观察、测量、抽象平行线分线段成比例定理,培养学生动手能力和直觉思维,在探究平行线判定相似的证明过程中,培养学生合情推理的能力及他们合作交流,积极探索与实践的良好习惯.
重点难点
重点:掌握平行线分线段成比例的基本事实,利用平行线判定相似三角形,能利用相似三角形性质解决边和角的计算问题.
难点:探究平行线判定相似三角形的方法.
教学设计
一、回顾旧知,
1.什么叫做相似图形?
2.什么叫做比例线段?比例有哪些性质?
3.相似多边形要满足哪些条件?相似多边形有哪些性质?
阅读课本
感受新知
1.对应角_________,对应边的比_________的两个三角形相似.如果△ABC~△,且△ABC与的相似比为k,则与△ABC的相似比为_______________.
2.平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段_______.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段______.
3.平行于三角形一边的直线与其他两边相交,所构成的三角形与原的三角形______.
三、探究新知
1.如图,已知,请分别度量在上截得的两条线段AB,
BC和在上截得的两条线段DE,
EF的长度,
AB:
BC与DE:EF相等吗?任意平移
,
(
(
图
1
)
)再量度,AB,
BC,
DE,
EF的长度,它们的比值还相等吗?
总结:
平行线分线段成比例定理:两条直线被一组平行线所截,所得到的________成比例.
2.(1)如果把图1中两条直线相交,交点A刚落到上,如图2所得的对应线段的比会相等吗?依据是什么?
(2)如果把图1中
两条直线相交,交点A刚落到上,
如图2(2)所得的对应线段的比会相等吗?依据是什么?
(
E
C
B
A
D
图
2
(
2
)
)
总结:
推论:平行于三角形一边的直线截其他两边(或两边的延长线),______________.
如图,在△ABC中,DE//BC,DE分别交AB、AC于点D、E,
(
A
D
E
B
C
)你能证明△ADE∽△ABC吗?
(
A
D
E
B
C
)(2)
如图,在△ABC中,DE//BC,DE分别交BA、CA的延长线于点D、E,
你能证明△ADE∽△ABC吗?
总结:平行于三角形一边的直线和其他两边(或两边的________)相交,所构成的三角形与原三角形相似.
四、应用新知
例:1
如图,在△ABC中,DE∥BC,AC=4
,AB=3,EC=1.
求AD和BD.
(
A
C
F
B
D
E
c
a
b
)练习:1.
如图,直线a//b//c,另两条直线分别交a、b、c
于点A、B、C及点D、E、F,且AB=3,DE=4,EF=2,则(
)
BC:DE=1:2
B.
BC:DE=2:3
C.
BC·DE=8
D.
BC·DE=6
2.如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论中正确的是(
)
A.
B.
C.
D.
(
mm
A
C
F
B
D
E
c
a
b
n
第
3
题
)3.如图,已知直线a//b//c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=________.
(
A
B
C
D
E
F
第
2
题
)
4.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
五、归纳小结,布置作业
课堂小结:1.平行线分线段成比例的基本事实是什么?推论是?
2.目前我们有什么方法判定两个三角形相似?
3.本课两个重要结论在探究中主要运用了哪些数学思想方法?
教学反思:
