第二十三章 旋转导学案
图片预览




文档简介
第二十三章 旋转
23.1 《图形的旋转》导学案
【学习目标】
1、知识与技能
了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.
2、过程与方法
感受生活中的几何,通过不同的情景设计归纳出图形旋转的有关概念,并用这些概念来解决一些问题.
3、情感态度与价值观
经历观察、操作等过程,了解图形旋转的概念,从事图形旋转基本性质的探索活动,进一步发展空间观察,培养运动几何的观点,增强审美意识.通过独立思考,自主探究和合作交流进一步体会旋转的数学内涵,获得知识,体验成功,享受学习乐趣.从事应用所学的知识进行图案设计的活动,享受成功的喜悦,激发学习热情。
【重难点、关键】
1、重点:旋转及对应点的有关概念及其应用。
2、难点与关键:从活生生的数学中抽出概念。
【学习课时】 1课时
【学习过程】
一、自主学习
完成教材56页“思考”
以上现象有什么共同特点?
二、合作展示
像这样,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的 ,点O叫做 ,转动的角叫做 。
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的 。
练习:如下四个图案,它们绕中心旋转一定的度数后都能和原来的图形相互重合,其中有一个图案与其余图案旋转的度数不同的是( )
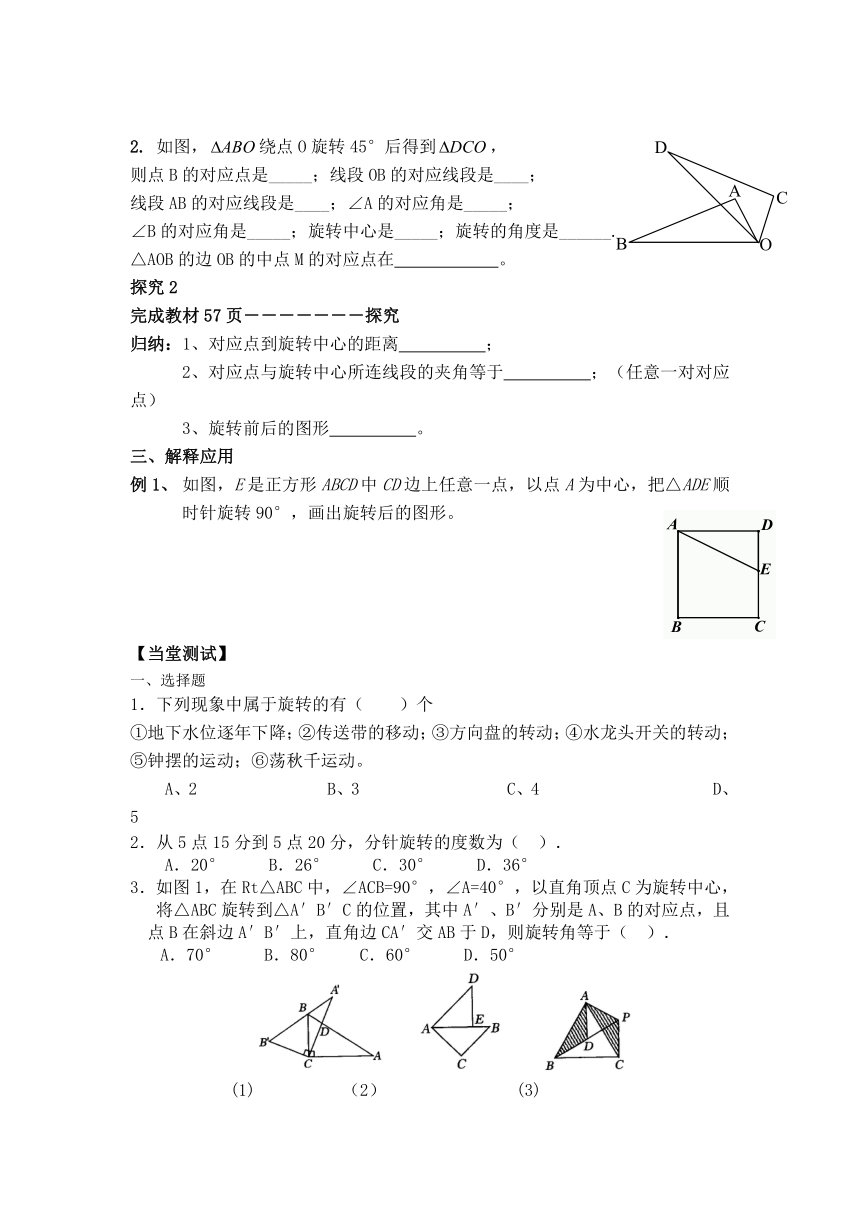
2. 如图,绕点O旋转45°后得到,
则点B的对应点是_____;线段OB的对应线段是____;
线段AB的对应线段是____;∠A的对应角是_____;
∠B的对应角是_____;旋转中心是_____;旋转的角度是______.
△AOB的边OB的中点M的对应点在 。
探究2
完成教材57页-------探究
归纳:1、对应点到旋转中心的距离 ;
2、对应点与旋转中心所连线段的夹角等于 ;(任意一对对应点)
3、旋转前后的图形 。
三、解释应用
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
【当堂测试】
一、选择题
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动。
A、2 B、3 C、4 D、5
2.从5点15分到5点20分,分针旋转的度数为( ).
A.20° B.26° C.30° D.36°
3.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ).
A.70° B.80° C.60° D.50°
(1) (2) (3)
二、填空题.
1.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是_____.
2.如图3,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是____;(2)旋转角度是____;(3)△ADP是______三角形.
三、综合提高题.
1.阅读下面材料:
如图4,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.
如图5,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.
(4) (5) (6)
如图6,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.
回答下列问题
如图7,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.
(1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?
(2)指出如图7所示中的线段BE与DF之间的关系.
2.一块等边三角形木块,边长为1,如图,现将木块沿水平线翻滚五个三角形,那么B点从开始至结束所走过的路径长是多少?
【课堂小结】
1、旋转的概念
2、旋转的性质
【作业】习题23.1第10题
【课后反思】
23.2.1 《中心对称》导学案
【学习目标】
1、通过具体实例认识中心对称,了解中心对称的概念
2、掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质
学习重点:中心对称的概念和性质
学习难点:理解中心对称的性质
【学习课时】 1课时
【学习过程】
活动一:复习回顾轴对称和旋转的有关知识
1、回忆什么是轴对称?成轴对称的两个图形有什么性质?
如果一个图形沿着_________对折后能与__________重合,则称这两个图形关于这条直线对称或轴对称。
成轴对称的图形,它们的对应点的连线被对称轴_________。
2、旋转有哪些性质?
对应点到旋转中心的距离___________对应点与旋转中心所连线段的夹角___________旋转前、后的图形___________。
活动二:自主学习----感知定义,探索性质
1、⑴把图①中一个图案绕点O旋转180°,你有什么发现?
⑵如图②,线段AC、BD相交于点O,OA=OC,OB=OD。把△OCD绕点O旋转180°,你有什么发现?
图① 图②
归纳:
中心对称的定义 ( http: / / www.xkb1.com ):一个图形绕着某一个点___________,如果它能与____________重合,就说这两个图形关于这个点对称或中心对称,这个点叫做___________,两个图形中的对应点叫做关于中心的_________。
活动三、 中心对称性质探索
动动手:(按下列步骤完成) 拿出三角板
⑴画出三角板内部的△ABC;
⑵以三角板的一个顶点O为中心,把三角板旋转180°,画出△AˊBˊCˊ;
⑶移开三角板;
得出:△ABC与△A'B'C'关于O点对称。
思考:⑴分别连接对称点AA'、BB'、CC'。点O在线段AA'上吗?如果在,在什么位置?
⑵ △ABC与△A'B'C'有什么关系?
归纳:
中心对称的性质:
中心对称的两个图形,对称点所连线段经过_________,而且被对称中心__________
中心对称的两个图形是________
活动四 中心对称画法探索
例1:⑴如图1,选择点O为对称中心,画出A点关于点O对称的点A'。
⑵如图2,选择点O为对称中心,画出与△ABC对称的△A'B'C'。
A
O
图1 图2
活动五:练习
1、如图,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在C′处,求CC′的长度。
2、如图,点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,过点O的直线分别交AD、BC于E、F,那么OE=OF吗?
【课堂小结】
1、中心对称的概念和性质
2、中心对称的画法
【作业】习题23.2第1、7题
【课后反思】
23.2.2 《中心对称图形》导学案
【学习目标】
了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
复习两个图形关于中心对称的有关概念,利用这个所学知识探索一个图形是中心对称图形的有关概念及其它的运用.
学习重点:中心对称图形的有关概念及其它们的运用。
学习难点:区别关于中心对称的两个图形和中心对称图形。
【学习课时】1课时
【学习过程】
一、复习引入
关于中心对称的两个图形具有什么性质?
二、探索新知
1、将线段AB绕着点中点旋转180°,你有什么发现?
2、将ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
归纳:
中心对称的定义:一个图形绕着某一个点___________,如果它能与____________重合,就说这两个图形关于这个点对称或中心对称,这个点叫做___________,两个图形中的对应点叫做关于中心的_________。
三、精讲精练
例:1.如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
2.在英文字母VWXYZ中,是中心对称的英文字母的个数有( )个.
A.1 B.2 C.3 D.4
3.下面的图案中,是中心对称图形的个数有( )个
A.1 B.2 C.3 D.4
【当堂测试】
一、选择题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.等腰梯形
C.平行四边形 D.正六边形
2.下列图形中,是中心对称图形,但不是轴对称图形的是( ).
A.正方形 B.矩形 C.菱形 D.平行四边形
3.如图所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是( )
A.21085 B.28015 C.58012 D.51082
二、填空题
1.把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做__________.
2.请你写出你所熟悉的三个中心对称图形_________.
3.中心对称图形具有什么特点(至少写出两个)_____________.
三、解答题
1.在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角,例如:正方形绕着它的对角线的交点旋转90°后能与自身重合,所以正方形是旋转对称图形,应有一个旋转角为90°.
(1)判断下列命题的真假(在相应括号内填上“真”或“假”)
①等腰梯形是旋转对称图形,它有一个旋转角为180°;( )
②矩形是旋转对称图形,它有一个旋转角为180°;( )
(2)填空:下列图形中是旋转对称图形,且有一个旋转角为120°是___ __.(写出所有正确结论的序号)
①正三角形;②正方形;③正六边形;④正八边形.
(3)写出两个多边形,它们都是旋转对称图形,却有一个旋转角为72°,并且分别满足下列条件:①是轴对称图形,但不是中心对称图形;②既是轴对称图形,又是中心对称图形.
【课堂小结】
1、中心对称图形的概念和性质
2、中心对称与中心对称图形的联系与区别。
【作业】习题23.2第2、8题
【课后反思】
23.2.3 《关于原点对称的点的坐标》导学案
【学习目标】
1、探究点(x,y)关于原点对称点的坐标,会运用发现的规律作关于原点对称的图形.
2、发展空间观念,渗透数形结合思想.
【学习重点】关于原点对称点的坐标.
【学习难点】探究关于原点对称点的坐标.
【学习课时】1课时
【学习过程】
一、基本训练,巩固旧知
1、如图,⑴画出点A关于x轴的对称点A′;
⑵画出点B关于x轴的对称点B′;
⑶画出点C关于y轴的对称点C′;
⑷画出点A关于y轴的对称点D′。
2、填空:
⑴点A(-2,1)关于x轴的对称点为A′( , );
⑵点B(0,-3)关于x轴的对称点为B′( , );
⑶点C(-4,-2)关于y轴的对称点为C′( , );
⑷点D(5,0)关于y轴的对称点为D′( , )。
二、创设情境,导入新课
归纳:点P(x,y)关于x轴的对称点为P′( , );
点P(x,y)关于y轴的对称点为P′( , );
三、合作探究
如图,A(3,2),B(-3,2),C(3,0),
⑴在直角坐标系中,画出点A,B,C关于原点
的对称点A′,B′,C′;
⑵点A(3,2)关于原点的对称点为A′( , )
点B(-3,2)关于原点的对称点为B′( , ),
点C(3,0)关于原点的对称点为C′( , );
归纳:两个点关于原点对称时,它们的坐标符号 ,即点P(x,y)关于原点的对称点P′( , ).
四、解释应用
例:如图,利用关于原点对称的点的坐标的特点,作出
与△ABC关于原点对称的图形。
课堂练习:
如图,在平面直角坐标系中A.B坐标分别为(2,0),(-1,3),若△OAC与△OAB全等,
⑴试尽可能多的写出点C的坐标;
⑴在⑴的结果中请找出与(1,0)成中心对称的两个点。
【当堂测试】
一、选择题
1.下列函数中,图象一定关于原点对称的图象是( )
A.y= B.y=2x+1 C.y=-2x+1 D.以上三种都不可能
2.如图,已知矩形ABCD周长为56cm,O是对称线交点,点O到矩形两条邻边的距离之差等于8cm,则矩形边长中较长的一边等于( ) A.8cm B.22cm C.24cm D.11cm
二、填空题
1.如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是P′_______.
2.写出函数y=-与y=具有的一个共同性质________(用对称的观点写).
三、综合提高题
1.如图,在平面直角坐标系中,A(-3,1),B(-2,3),
C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出
△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系,请说明理由.
【课堂小结】
关于原点对称点的坐标特征
【作业】习题23.2第3、 9题
【课后反思】
23.3.3《 课题学习 图案设计》导学案
【学习目标】
利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案.
2、通过复习平移、轴对称、旋转的知识,0然后利用这些知识让学生开动脑筋,敝开胸怀大胆联想,设计出一幅幅美丽的图案.
【学习重点】设计图案.
【学习难点】如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
【学习课时】1课时
【学习过程】
活动1:
在生活中,我们经常见到一些美丽的图案:
1、你能用平移、旋转或轴对称分析如图中各个图案的形成过程吗?
2、归纳以上图形变换的共性:
活动2:
观察教科书图23.3-1,分析它是将哪种基本图形经过了哪些变换后得到的?
观察上述图案,感受简单图案的丰富变换。
活动3:
展示学生课前搜集到的利用平移、旋转和轴对称变换设计的组合图案。
⑴剪纸中的三种变换;
⑵艺术图案中的三种变换;
⑶电脑设计出的图案变换。
思考:进行图案设计的步骤是什么?
活动4:
分组进行组合图案的设计,
活动5:
1、展示确定的基本图案及变换出的组合图案。
2、简单说明你的图案设计中运用了哪些图形变换?
活动6:
归纳提升: 欣赏变换所产生的美。
【当堂测试】
一、选择题
1.在图所示的4个图案中既包含图形的旋转,还有图形轴对称是( )
2.将三角形绕直线L旋转一周,可以得到如图所示的立体图形的是( )
二、填空题
1.基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
2.如上右图,是由________关系得到的图形.
3如图,你能利用平移、旋转或轴对称这样的变化过程来分析它的形成过程吗?
【课堂小结】
如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
【课后反思】
B
A
C
O
A
B
23.1 《图形的旋转》导学案
【学习目标】
1、知识与技能
了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.
2、过程与方法
感受生活中的几何,通过不同的情景设计归纳出图形旋转的有关概念,并用这些概念来解决一些问题.
3、情感态度与价值观
经历观察、操作等过程,了解图形旋转的概念,从事图形旋转基本性质的探索活动,进一步发展空间观察,培养运动几何的观点,增强审美意识.通过独立思考,自主探究和合作交流进一步体会旋转的数学内涵,获得知识,体验成功,享受学习乐趣.从事应用所学的知识进行图案设计的活动,享受成功的喜悦,激发学习热情。
【重难点、关键】
1、重点:旋转及对应点的有关概念及其应用。
2、难点与关键:从活生生的数学中抽出概念。
【学习课时】 1课时
【学习过程】
一、自主学习
完成教材56页“思考”
以上现象有什么共同特点?
二、合作展示
像这样,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的 ,点O叫做 ,转动的角叫做 。
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的 。
练习:如下四个图案,它们绕中心旋转一定的度数后都能和原来的图形相互重合,其中有一个图案与其余图案旋转的度数不同的是( )
2. 如图,绕点O旋转45°后得到,
则点B的对应点是_____;线段OB的对应线段是____;
线段AB的对应线段是____;∠A的对应角是_____;
∠B的对应角是_____;旋转中心是_____;旋转的角度是______.
△AOB的边OB的中点M的对应点在 。
探究2
完成教材57页-------探究
归纳:1、对应点到旋转中心的距离 ;
2、对应点与旋转中心所连线段的夹角等于 ;(任意一对对应点)
3、旋转前后的图形 。
三、解释应用
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
【当堂测试】
一、选择题
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动。
A、2 B、3 C、4 D、5
2.从5点15分到5点20分,分针旋转的度数为( ).
A.20° B.26° C.30° D.36°
3.如图1,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ).
A.70° B.80° C.60° D.50°
(1) (2) (3)
二、填空题.
1.如图2,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是_____.
2.如图3,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是____;(2)旋转角度是____;(3)△ADP是______三角形.
三、综合提高题.
1.阅读下面材料:
如图4,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.
如图5,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.
(4) (5) (6)
如图6,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.
回答下列问题
如图7,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.
(1)在如图7所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?
(2)指出如图7所示中的线段BE与DF之间的关系.
2.一块等边三角形木块,边长为1,如图,现将木块沿水平线翻滚五个三角形,那么B点从开始至结束所走过的路径长是多少?
【课堂小结】
1、旋转的概念
2、旋转的性质
【作业】习题23.1第10题
【课后反思】
23.2.1 《中心对称》导学案
【学习目标】
1、通过具体实例认识中心对称,了解中心对称的概念
2、掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质
学习重点:中心对称的概念和性质
学习难点:理解中心对称的性质
【学习课时】 1课时
【学习过程】
活动一:复习回顾轴对称和旋转的有关知识
1、回忆什么是轴对称?成轴对称的两个图形有什么性质?
如果一个图形沿着_________对折后能与__________重合,则称这两个图形关于这条直线对称或轴对称。
成轴对称的图形,它们的对应点的连线被对称轴_________。
2、旋转有哪些性质?
对应点到旋转中心的距离___________对应点与旋转中心所连线段的夹角___________旋转前、后的图形___________。
活动二:自主学习----感知定义,探索性质
1、⑴把图①中一个图案绕点O旋转180°,你有什么发现?
⑵如图②,线段AC、BD相交于点O,OA=OC,OB=OD。把△OCD绕点O旋转180°,你有什么发现?
图① 图②
归纳:
中心对称的定义 ( http: / / www.xkb1.com ):一个图形绕着某一个点___________,如果它能与____________重合,就说这两个图形关于这个点对称或中心对称,这个点叫做___________,两个图形中的对应点叫做关于中心的_________。
活动三、 中心对称性质探索
动动手:(按下列步骤完成) 拿出三角板
⑴画出三角板内部的△ABC;
⑵以三角板的一个顶点O为中心,把三角板旋转180°,画出△AˊBˊCˊ;
⑶移开三角板;
得出:△ABC与△A'B'C'关于O点对称。
思考:⑴分别连接对称点AA'、BB'、CC'。点O在线段AA'上吗?如果在,在什么位置?
⑵ △ABC与△A'B'C'有什么关系?
归纳:
中心对称的性质:
中心对称的两个图形,对称点所连线段经过_________,而且被对称中心__________
中心对称的两个图形是________
活动四 中心对称画法探索
例1:⑴如图1,选择点O为对称中心,画出A点关于点O对称的点A'。
⑵如图2,选择点O为对称中心,画出与△ABC对称的△A'B'C'。
A
O
图1 图2
活动五:练习
1、如图,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在C′处,求CC′的长度。
2、如图,点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,过点O的直线分别交AD、BC于E、F,那么OE=OF吗?
【课堂小结】
1、中心对称的概念和性质
2、中心对称的画法
【作业】习题23.2第1、7题
【课后反思】
23.2.2 《中心对称图形》导学案
【学习目标】
了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
复习两个图形关于中心对称的有关概念,利用这个所学知识探索一个图形是中心对称图形的有关概念及其它的运用.
学习重点:中心对称图形的有关概念及其它们的运用。
学习难点:区别关于中心对称的两个图形和中心对称图形。
【学习课时】1课时
【学习过程】
一、复习引入
关于中心对称的两个图形具有什么性质?
二、探索新知
1、将线段AB绕着点中点旋转180°,你有什么发现?
2、将ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
归纳:
中心对称的定义:一个图形绕着某一个点___________,如果它能与____________重合,就说这两个图形关于这个点对称或中心对称,这个点叫做___________,两个图形中的对应点叫做关于中心的_________。
三、精讲精练
例:1.如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
2.在英文字母VWXYZ中,是中心对称的英文字母的个数有( )个.
A.1 B.2 C.3 D.4
3.下面的图案中,是中心对称图形的个数有( )个
A.1 B.2 C.3 D.4
【当堂测试】
一、选择题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.等腰梯形
C.平行四边形 D.正六边形
2.下列图形中,是中心对称图形,但不是轴对称图形的是( ).
A.正方形 B.矩形 C.菱形 D.平行四边形
3.如图所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是( )
A.21085 B.28015 C.58012 D.51082
二、填空题
1.把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做__________.
2.请你写出你所熟悉的三个中心对称图形_________.
3.中心对称图形具有什么特点(至少写出两个)_____________.
三、解答题
1.在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角,例如:正方形绕着它的对角线的交点旋转90°后能与自身重合,所以正方形是旋转对称图形,应有一个旋转角为90°.
(1)判断下列命题的真假(在相应括号内填上“真”或“假”)
①等腰梯形是旋转对称图形,它有一个旋转角为180°;( )
②矩形是旋转对称图形,它有一个旋转角为180°;( )
(2)填空:下列图形中是旋转对称图形,且有一个旋转角为120°是___ __.(写出所有正确结论的序号)
①正三角形;②正方形;③正六边形;④正八边形.
(3)写出两个多边形,它们都是旋转对称图形,却有一个旋转角为72°,并且分别满足下列条件:①是轴对称图形,但不是中心对称图形;②既是轴对称图形,又是中心对称图形.
【课堂小结】
1、中心对称图形的概念和性质
2、中心对称与中心对称图形的联系与区别。
【作业】习题23.2第2、8题
【课后反思】
23.2.3 《关于原点对称的点的坐标》导学案
【学习目标】
1、探究点(x,y)关于原点对称点的坐标,会运用发现的规律作关于原点对称的图形.
2、发展空间观念,渗透数形结合思想.
【学习重点】关于原点对称点的坐标.
【学习难点】探究关于原点对称点的坐标.
【学习课时】1课时
【学习过程】
一、基本训练,巩固旧知
1、如图,⑴画出点A关于x轴的对称点A′;
⑵画出点B关于x轴的对称点B′;
⑶画出点C关于y轴的对称点C′;
⑷画出点A关于y轴的对称点D′。
2、填空:
⑴点A(-2,1)关于x轴的对称点为A′( , );
⑵点B(0,-3)关于x轴的对称点为B′( , );
⑶点C(-4,-2)关于y轴的对称点为C′( , );
⑷点D(5,0)关于y轴的对称点为D′( , )。
二、创设情境,导入新课
归纳:点P(x,y)关于x轴的对称点为P′( , );
点P(x,y)关于y轴的对称点为P′( , );
三、合作探究
如图,A(3,2),B(-3,2),C(3,0),
⑴在直角坐标系中,画出点A,B,C关于原点
的对称点A′,B′,C′;
⑵点A(3,2)关于原点的对称点为A′( , )
点B(-3,2)关于原点的对称点为B′( , ),
点C(3,0)关于原点的对称点为C′( , );
归纳:两个点关于原点对称时,它们的坐标符号 ,即点P(x,y)关于原点的对称点P′( , ).
四、解释应用
例:如图,利用关于原点对称的点的坐标的特点,作出
与△ABC关于原点对称的图形。
课堂练习:
如图,在平面直角坐标系中A.B坐标分别为(2,0),(-1,3),若△OAC与△OAB全等,
⑴试尽可能多的写出点C的坐标;
⑴在⑴的结果中请找出与(1,0)成中心对称的两个点。
【当堂测试】
一、选择题
1.下列函数中,图象一定关于原点对称的图象是( )
A.y= B.y=2x+1 C.y=-2x+1 D.以上三种都不可能
2.如图,已知矩形ABCD周长为56cm,O是对称线交点,点O到矩形两条邻边的距离之差等于8cm,则矩形边长中较长的一边等于( ) A.8cm B.22cm C.24cm D.11cm
二、填空题
1.如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是P′_______.
2.写出函数y=-与y=具有的一个共同性质________(用对称的观点写).
三、综合提高题
1.如图,在平面直角坐标系中,A(-3,1),B(-2,3),
C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出
△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系,请说明理由.
【课堂小结】
关于原点对称点的坐标特征
【作业】习题23.2第3、 9题
【课后反思】
23.3.3《 课题学习 图案设计》导学案
【学习目标】
利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案.
2、通过复习平移、轴对称、旋转的知识,0然后利用这些知识让学生开动脑筋,敝开胸怀大胆联想,设计出一幅幅美丽的图案.
【学习重点】设计图案.
【学习难点】如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
【学习课时】1课时
【学习过程】
活动1:
在生活中,我们经常见到一些美丽的图案:
1、你能用平移、旋转或轴对称分析如图中各个图案的形成过程吗?
2、归纳以上图形变换的共性:
活动2:
观察教科书图23.3-1,分析它是将哪种基本图形经过了哪些变换后得到的?
观察上述图案,感受简单图案的丰富变换。
活动3:
展示学生课前搜集到的利用平移、旋转和轴对称变换设计的组合图案。
⑴剪纸中的三种变换;
⑵艺术图案中的三种变换;
⑶电脑设计出的图案变换。
思考:进行图案设计的步骤是什么?
活动4:
分组进行组合图案的设计,
活动5:
1、展示确定的基本图案及变换出的组合图案。
2、简单说明你的图案设计中运用了哪些图形变换?
活动6:
归纳提升: 欣赏变换所产生的美。
【当堂测试】
一、选择题
1.在图所示的4个图案中既包含图形的旋转,还有图形轴对称是( )
2.将三角形绕直线L旋转一周,可以得到如图所示的立体图形的是( )
二、填空题
1.基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
2.如上右图,是由________关系得到的图形.
3如图,你能利用平移、旋转或轴对称这样的变化过程来分析它的形成过程吗?
【课堂小结】
如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
【课后反思】
B
A
C
O
A
B
同课章节目录
