第22章二次函数第3课时二次函数 y = ax?+k 的图象及性质-人教版九年级数学上册讲义(机构专用)(word含答案)
文档属性
| 名称 | 第22章二次函数第3课时二次函数 y = ax?+k 的图象及性质-人教版九年级数学上册讲义(机构专用)(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览


文档简介
人
教
版
九
年
级
数
学
上
册
讲
义
第二十二章
二次函数
第3课时二次函数
教学目的
会用描点法画出二次函数
y
=
ax??
+k
的图象.
通过二次函数
y
=
ax???
+k的图象,了解它们的图象特征和性质.
教学重点
教学内容
知识要点1.二次函数y=ax2+k(a≠0)的图象和性质形 状:抛物线.对称轴:y轴.顶点坐标:(0,k).开口方向:a>0,开口向上;a<0,开口向下.最 值:a>0,当x=
0
时,y最小值=k;a<0,当x=
0
时,y最大值=k.2.抛物线y=ax2+k与y=ax2的关系相同点:形状、大小,开口方向相同.不同点:顶点及位置不同.平移规律:y=ax2
y=ax2+k;
y=ax2
y=ax2-k.对应练习1.抛物线y=x2﹣2的顶点坐标是( )A.?(0,2)B.?(0,﹣2)C.?(﹣2,0)D.?(2,0)2.已知点A(﹣2,y1),B(2,y2),C(5,y3)在二次函数y=﹣3x2+k图象上,则y1,y2,y3的大小关系是( )A.?y1<y2<y3B.?y1<y2<y3C.?y1=y2>y3D.?y1=y2<y33.在同一直角坐标系中,函数?与?的图像大致如图(
)A.?B.??C.??D.?4.二次函数满足下列条件:①函数有最大值3;②对称轴为y轴,写出一个满足以上条件的二次函数解析式:????5.抛物线y=x2-1的顶点坐标是????.课后作业1.抛物线y=﹣?x2+1的顶点坐标是(
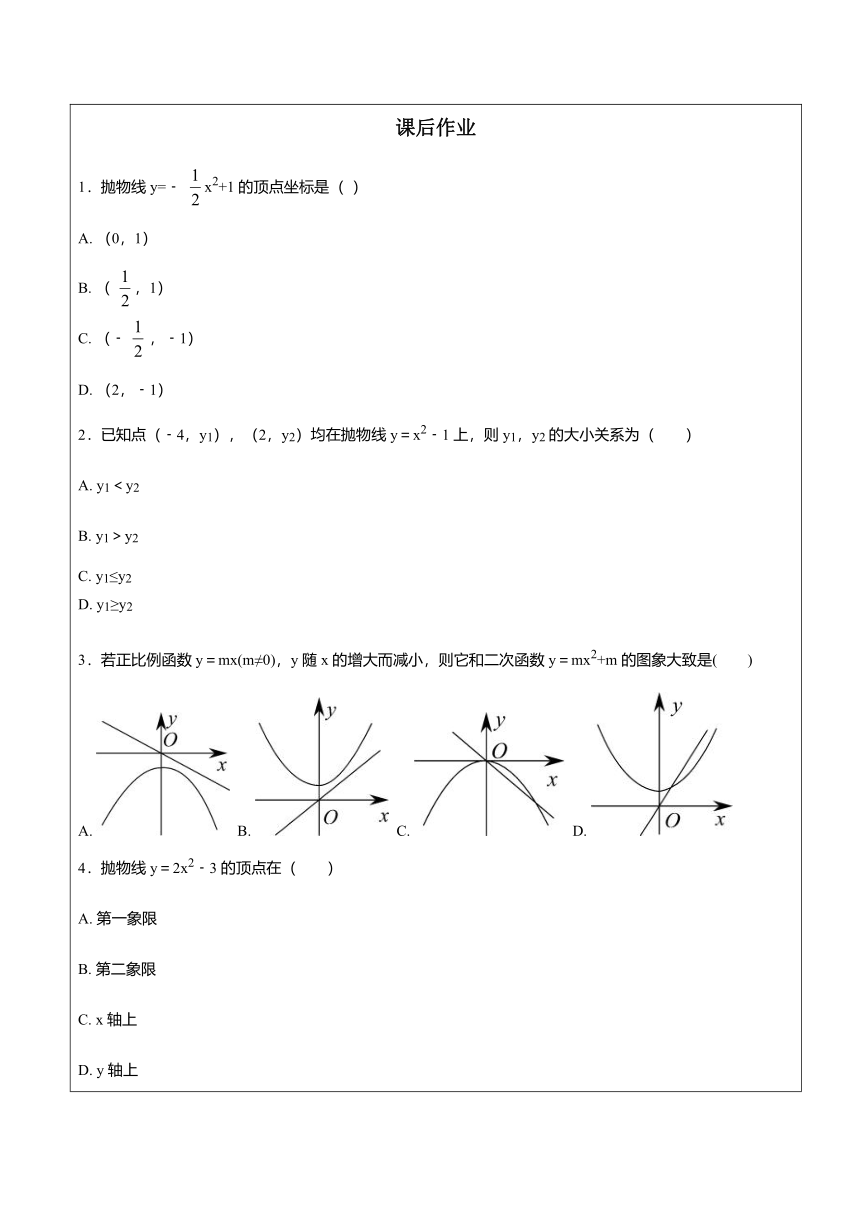
)A.?(0,1)?B.?(?,1)?C.?(﹣?,﹣1)?D.?(2,﹣1)2.已知点(﹣4,y1),(2,y2)均在抛物线y=x2﹣1上,则y1,y2的大小关系为( )A.?y1<y2B.?y1>y2C.?y1≤y2D.?y1≥y23.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A.?
B.?
C.?
D.?4.抛物线y=2x2﹣3的顶点在( )A.?第一象限B.?第二象限C.?x轴上D.?y轴上5.在同一直角坐标系中?与?(a≠0,b≠0)图象大致为??A.?
B.?
C.?
D.?6.已知A(﹣1,y1),B(,y2),C(2,y3)三点都在二次函数y=ax2﹣1(a>0)的图象上,那么y1,y2,y3的大小关系是
(用"<"连接)7.平面直角坐标系中,二次函数y=x2+1的图象的顶点坐标为
.8.抛物线y=4x2﹣3的顶点坐标是????.9.在同一直角坐标系中,画出函数y=2x2+1,y=2x2-1的图像.
练习答案:BCC答案不唯一y=﹣x2+3(0,-1)
作业答案:ABADAy1<y2<y3(0,1)(0,-3)解:先列表:
然后描点画图,得y=2x2+1,y=2x2-1的图像
教
版
九
年
级
数
学
上
册
讲
义
第二十二章
二次函数
第3课时二次函数
教学目的
会用描点法画出二次函数
y
=
ax??
+k
的图象.
通过二次函数
y
=
ax???
+k的图象,了解它们的图象特征和性质.
教学重点
教学内容
知识要点1.二次函数y=ax2+k(a≠0)的图象和性质形 状:抛物线.对称轴:y轴.顶点坐标:(0,k).开口方向:a>0,开口向上;a<0,开口向下.最 值:a>0,当x=
0
时,y最小值=k;a<0,当x=
0
时,y最大值=k.2.抛物线y=ax2+k与y=ax2的关系相同点:形状、大小,开口方向相同.不同点:顶点及位置不同.平移规律:y=ax2
y=ax2+k;
y=ax2
y=ax2-k.对应练习1.抛物线y=x2﹣2的顶点坐标是( )A.?(0,2)B.?(0,﹣2)C.?(﹣2,0)D.?(2,0)2.已知点A(﹣2,y1),B(2,y2),C(5,y3)在二次函数y=﹣3x2+k图象上,则y1,y2,y3的大小关系是( )A.?y1<y2<y3B.?y1<y2<y3C.?y1=y2>y3D.?y1=y2<y33.在同一直角坐标系中,函数?与?的图像大致如图(
)A.?B.??C.??D.?4.二次函数满足下列条件:①函数有最大值3;②对称轴为y轴,写出一个满足以上条件的二次函数解析式:????5.抛物线y=x2-1的顶点坐标是????.课后作业1.抛物线y=﹣?x2+1的顶点坐标是(
)A.?(0,1)?B.?(?,1)?C.?(﹣?,﹣1)?D.?(2,﹣1)2.已知点(﹣4,y1),(2,y2)均在抛物线y=x2﹣1上,则y1,y2的大小关系为( )A.?y1<y2B.?y1>y2C.?y1≤y2D.?y1≥y23.若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A.?
B.?
C.?
D.?4.抛物线y=2x2﹣3的顶点在( )A.?第一象限B.?第二象限C.?x轴上D.?y轴上5.在同一直角坐标系中?与?(a≠0,b≠0)图象大致为??A.?
B.?
C.?
D.?6.已知A(﹣1,y1),B(,y2),C(2,y3)三点都在二次函数y=ax2﹣1(a>0)的图象上,那么y1,y2,y3的大小关系是
(用"<"连接)7.平面直角坐标系中,二次函数y=x2+1的图象的顶点坐标为
.8.抛物线y=4x2﹣3的顶点坐标是????.9.在同一直角坐标系中,画出函数y=2x2+1,y=2x2-1的图像.
练习答案:BCC答案不唯一y=﹣x2+3(0,-1)
作业答案:ABADAy1<y2<y3(0,1)(0,-3)解:先列表:
然后描点画图,得y=2x2+1,y=2x2-1的图像
同课章节目录
