苏科版数学八年级下册 9.4.1矩形 教案
文档属性
| 名称 | 苏科版数学八年级下册 9.4.1矩形 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 111.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:15:38 | ||
图片预览

文档简介
9.4矩形
学习目标:1掌握矩形的概念,探索矩形的性质;
2能运用矩形的性质解决一些简单的问题。
【重点难点】
重点:矩形的判定方法的理解和掌握。
难点:矩形的判定方法的综合应用。
概念引入
1.矩形的概念(如图1)
有一个角是_______的平行四边形叫做矩形.矩形是特殊的_______四边形.
2.矩形的性质(如图2)
ABCD的其他的三个内角为 度.
对角线AC、BD的大小有什么关系?请加以证明
矩形是中心对称图形吗?是轴对称图形吗?
如图2,在矩形ABCD中有 个等腰三角形,并说明理由
归纳:矩形的四个角 ,对角线 ;
矩形既是 图形,也是 图形。
例1. 如图矩形ABCD的对称线相交于点O,AB=2cm,∠AOB=60°
(1)求对角线AC的长.(2)求矩形ABCD的周长
例2.如图 在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,如果FE⊥AE,求证:FE=AE.
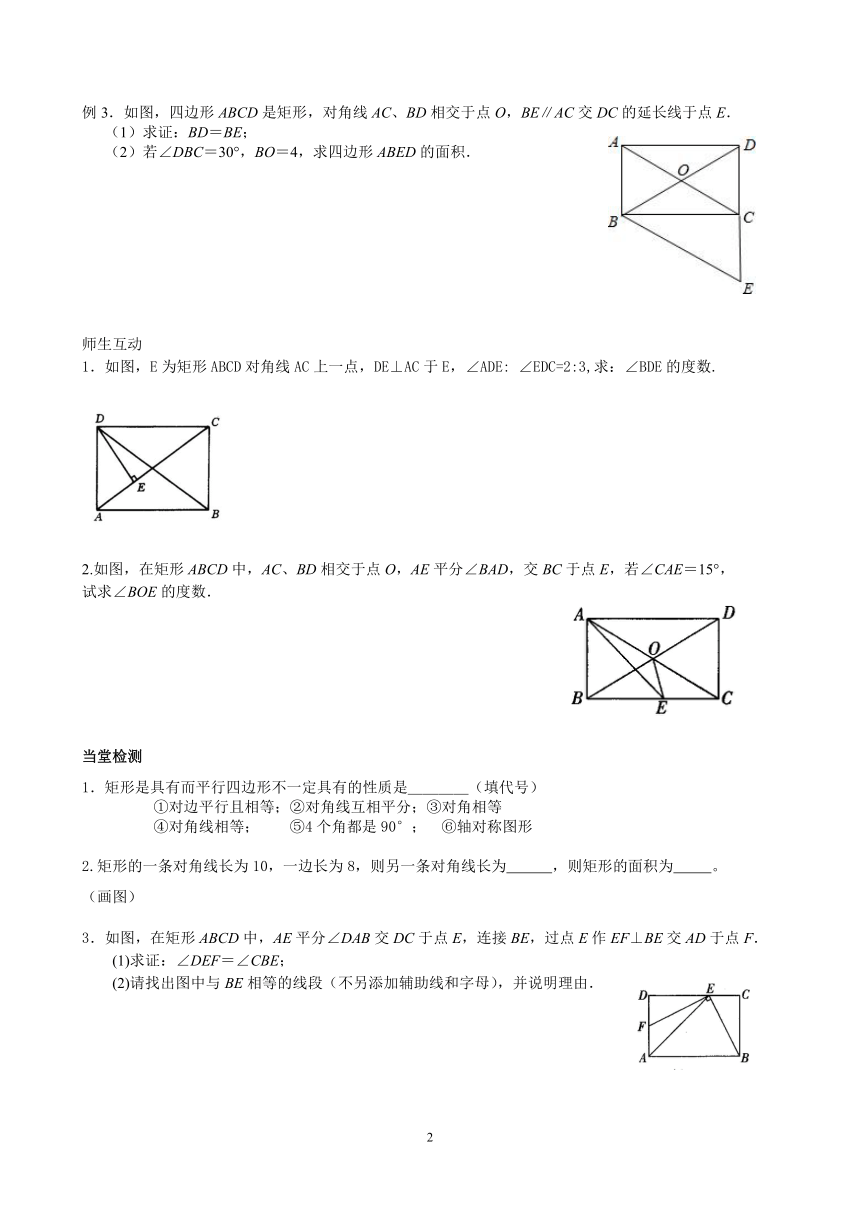
例3.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
师生互动
1.如图,E为矩形ABCD对角线AC上一点,DE⊥AC于E,∠ADE: ∠EDC=2:3,求:∠BDE的度数.
2.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于点E,若∠CAE=15°,
试求∠BOE的度数.
当堂检测
1.矩形是具有而平行四边形不一定具有的性质是____(填代号)
①对边平行且相等;②对角线互相平分;③对角相等
④对角线相等; ⑤4个角都是90°; ⑥轴对称图形
2.矩形的一条对角线长为10,一边长为8,则另一条对角线长为 ,则矩形的面积为 。
(画图)
3.如图,在矩形ABCD中,AE平分∠DAB交DC于点E,连接BE,过点E作EF⊥BE交AD于点F.
(1)求证:∠DEF=∠CBE;
(2)请找出图中与BE相等的线段(不另添加辅助线和字母),并说明理由.
提补作业
1. 在矩形ABCD中, ∠AOB=120°,AD=3,则AC为( )
A. 1.5 B. 3 C. 6 D. 9
2.直角三角形斜边上的高与中线分别是5和6,则它的面积是_______________.
3. 矩形的两条对角线的夹角为60°,较短的边长为4.5厘米,则对角线长为 。
4.如图矩形ABCD中,若AB=4,BC=9,E、F分别为BC,DA上的点,则S四边形AECF等于( )
A.12 B.24 C.36 D.48
5. 如图,EF过矩形对角线的交点O,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
(第4题) (第5题)
6. 如图,在矩形ABCD中,点E在AD上,EC平分∠BED。
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=1,∠ABE=45°,求BC的长
7. 已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.
求证:BE=CF.
8.如图,矩形ABCD中,点F是BC上的一点,且AE=BC,AE⊥DF于点E,
求证:EF=CE
9.在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于点O,
⑴若BE:ED=1:3,AD=6cm,求AE的长;
⑵若∠EAB:∠EAD=1:2,且BD=10,求AE的长.
11.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,求PE+PF的值
4
学习目标:1掌握矩形的概念,探索矩形的性质;
2能运用矩形的性质解决一些简单的问题。
【重点难点】
重点:矩形的判定方法的理解和掌握。
难点:矩形的判定方法的综合应用。
概念引入
1.矩形的概念(如图1)
有一个角是_______的平行四边形叫做矩形.矩形是特殊的_______四边形.
2.矩形的性质(如图2)
ABCD的其他的三个内角为 度.
对角线AC、BD的大小有什么关系?请加以证明
矩形是中心对称图形吗?是轴对称图形吗?
如图2,在矩形ABCD中有 个等腰三角形,并说明理由
归纳:矩形的四个角 ,对角线 ;
矩形既是 图形,也是 图形。
例1. 如图矩形ABCD的对称线相交于点O,AB=2cm,∠AOB=60°
(1)求对角线AC的长.(2)求矩形ABCD的周长
例2.如图 在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,如果FE⊥AE,求证:FE=AE.
例3.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
师生互动
1.如图,E为矩形ABCD对角线AC上一点,DE⊥AC于E,∠ADE: ∠EDC=2:3,求:∠BDE的度数.
2.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于点E,若∠CAE=15°,
试求∠BOE的度数.
当堂检测
1.矩形是具有而平行四边形不一定具有的性质是____(填代号)
①对边平行且相等;②对角线互相平分;③对角相等
④对角线相等; ⑤4个角都是90°; ⑥轴对称图形
2.矩形的一条对角线长为10,一边长为8,则另一条对角线长为 ,则矩形的面积为 。
(画图)
3.如图,在矩形ABCD中,AE平分∠DAB交DC于点E,连接BE,过点E作EF⊥BE交AD于点F.
(1)求证:∠DEF=∠CBE;
(2)请找出图中与BE相等的线段(不另添加辅助线和字母),并说明理由.
提补作业
1. 在矩形ABCD中, ∠AOB=120°,AD=3,则AC为( )
A. 1.5 B. 3 C. 6 D. 9
2.直角三角形斜边上的高与中线分别是5和6,则它的面积是_______________.
3. 矩形的两条对角线的夹角为60°,较短的边长为4.5厘米,则对角线长为 。
4.如图矩形ABCD中,若AB=4,BC=9,E、F分别为BC,DA上的点,则S四边形AECF等于( )
A.12 B.24 C.36 D.48
5. 如图,EF过矩形对角线的交点O,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
(第4题) (第5题)
6. 如图,在矩形ABCD中,点E在AD上,EC平分∠BED。
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=1,∠ABE=45°,求BC的长
7. 已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.
求证:BE=CF.
8.如图,矩形ABCD中,点F是BC上的一点,且AE=BC,AE⊥DF于点E,
求证:EF=CE
9.在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于点O,
⑴若BE:ED=1:3,AD=6cm,求AE的长;
⑵若∠EAB:∠EAD=1:2,且BD=10,求AE的长.
11.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,求PE+PF的值
4
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
