苏科版数学八年级下册 9.4.3正方形 教案
文档属性
| 名称 | 苏科版数学八年级下册 9.4.3正方形 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览

文档简介
9.4正方形
【教学目标]
1、会归纳正方形的特性并进行证明
2、能运用正方形的性质定理进行简单的计算与证明
3、在进行探索、猜想、证明的过程中,进一步体会证明的必要性以及计算与证明在解决问题中的作用
4、在比较、归纳、总结的过程中,进一步体会特殊与一般之间的辩证关系
【教学重、难点】
1.经历观察、实验、猜想、证明等活动,发展合情推理能力和初步的演绎推理能力
2.有条理地、清晰地阐述自己的观点
【情境创设 】
这是一个流传在世界各地的故事,三姐妹的父亲是一位慈祥的阿拉伯老人。一天,老人不幸去世,临终,老人留给三个女儿一件珍贵的传家宝——一块五色斑斓的正方形地毯,深爱父亲的女儿们都想得这块地毯,以作纪念。大姐想出了一个好办法:“把它裁成三个小正方形地毯,为了不使地毯剪得过于零碎,最好只剪成4块,其中两块是正方形,另外两块可以拼成一个正方形。”聪明的你能想出一个巧妙的剪法,符合大姐的设想吗?
【合作交流】
探索正方形的性质
(1)边的性质: ;
(2)角的性质: ;
(3)对角线的性质: ;
(4)对称性: 。
【典题选讲】
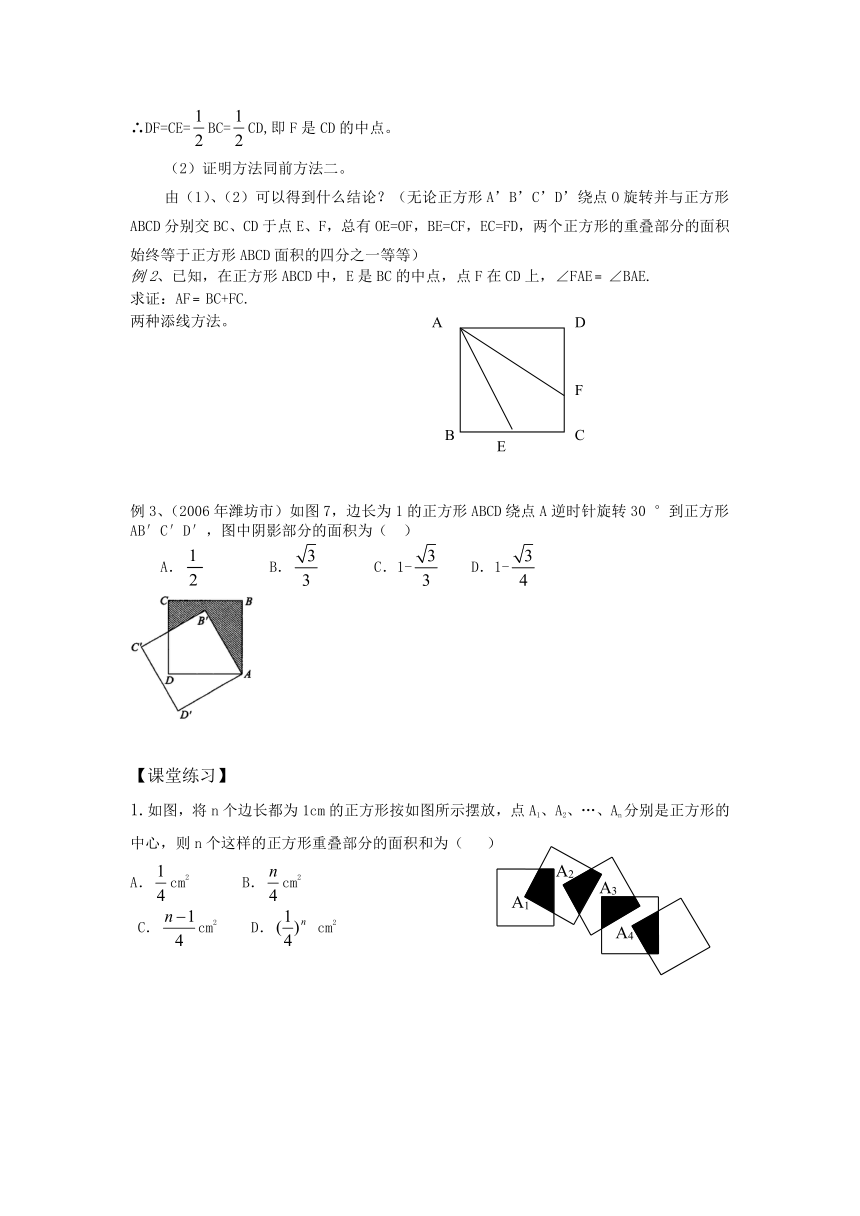
例1、 已知:如图,正方形ABCD的对角线AC、BD相交于点O;正方形A’B’C’D’的顶点A’与点O重合,A’B’交BC于点E,A’D’交CD于点F,E是BC的中点。
(1)求证:F是CD的中点
(2)若正方形A’B’C’D’绕点O任意旋转某个角度后,OE=OF吗?
分析:(1)方法一∵OB=OC,E是BC的中点
∴OE⊥BC,∠OEC=90°
∵∠EA’F=∠ECF=90°
∴∠OFC=90°
∵OC=OD
∴F是CD的中点
方法二 ∵∠EA’F=90°,AC⊥BD
∴∠EOC+∠COF=∠DOF+∠COF=90°
∴∠EOC=∠DOF
又OC=OD,∠OCE=∠ODF=45°
∴△OCE≌△ODF(ASA)
∴DF=CE=BC=CD,即F是CD的中点。
(2)证明方法同前方法二。
由(1)、(2)可以得到什么结论?(无论正方形A’B’C’D’绕点O旋转并与正方形ABCD分别交BC、CD于点E、F,总有OE=OF,BE=CF,EC=FD,两个正方形的重叠部分的面积始终等于正方形ABCD面积的四分之一等等)
例2、已知,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE﹦∠BAE.
求证:AF﹦BC+FC.
两种添线方法。
例3、(2006年潍坊市)如图7,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
A. B. C.1- D.1-
【课堂练习】
1.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
A.cm2 B.cm2
C.cm2 D. cm2
2、已知正方形ABCD。
(1)如图1,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H,求证:BE=GH;
(2)如图2,过正方形ABCD内任意一点作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,EF与GH相等吗?请写出你的结论;
(3)当点O在正方形ABCD的边上或外部时,过点O作两条互相垂直的直线,被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗?其中一种情形如图3所示,过正方形ABCD外一点O作互相垂直的两条直线m、n,m与AD、BC的延长线分别交于点E、F,n与AB、DC的延长线分别交于点G、H,试就该图对你的结论加以证明。
练习:
3、现有若干张边长不相等但都大于4cm的正方形纸片,从中任选一张,如图从距离正方形的四个顶点2cm处,沿45°角画线,将正方形纸片分成5部分,则中间阴影部分的面积是 cm;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律? .
【学习体会】
正方形与矩形,菱形,平行四边形的关系如下图。(请填写它们之间的关系)
(2)正方形的性质:
①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形既是轴对称图形,又是中心对称图形。
⑤正方形对角线相等,互相垂直平分,每条对角线平分一组对
(3)本节课我们把探索和解决问题的思路、方法、结论,从特殊情形逐步推广到一般的情形,从而得到一般的结论,这也是我们获得数学结论的一种重要的思想方法。
【教学目标]
1、会归纳正方形的特性并进行证明
2、能运用正方形的性质定理进行简单的计算与证明
3、在进行探索、猜想、证明的过程中,进一步体会证明的必要性以及计算与证明在解决问题中的作用
4、在比较、归纳、总结的过程中,进一步体会特殊与一般之间的辩证关系
【教学重、难点】
1.经历观察、实验、猜想、证明等活动,发展合情推理能力和初步的演绎推理能力
2.有条理地、清晰地阐述自己的观点
【情境创设 】
这是一个流传在世界各地的故事,三姐妹的父亲是一位慈祥的阿拉伯老人。一天,老人不幸去世,临终,老人留给三个女儿一件珍贵的传家宝——一块五色斑斓的正方形地毯,深爱父亲的女儿们都想得这块地毯,以作纪念。大姐想出了一个好办法:“把它裁成三个小正方形地毯,为了不使地毯剪得过于零碎,最好只剪成4块,其中两块是正方形,另外两块可以拼成一个正方形。”聪明的你能想出一个巧妙的剪法,符合大姐的设想吗?
【合作交流】
探索正方形的性质
(1)边的性质: ;
(2)角的性质: ;
(3)对角线的性质: ;
(4)对称性: 。
【典题选讲】
例1、 已知:如图,正方形ABCD的对角线AC、BD相交于点O;正方形A’B’C’D’的顶点A’与点O重合,A’B’交BC于点E,A’D’交CD于点F,E是BC的中点。
(1)求证:F是CD的中点
(2)若正方形A’B’C’D’绕点O任意旋转某个角度后,OE=OF吗?
分析:(1)方法一∵OB=OC,E是BC的中点
∴OE⊥BC,∠OEC=90°
∵∠EA’F=∠ECF=90°
∴∠OFC=90°
∵OC=OD
∴F是CD的中点
方法二 ∵∠EA’F=90°,AC⊥BD
∴∠EOC+∠COF=∠DOF+∠COF=90°
∴∠EOC=∠DOF
又OC=OD,∠OCE=∠ODF=45°
∴△OCE≌△ODF(ASA)
∴DF=CE=BC=CD,即F是CD的中点。
(2)证明方法同前方法二。
由(1)、(2)可以得到什么结论?(无论正方形A’B’C’D’绕点O旋转并与正方形ABCD分别交BC、CD于点E、F,总有OE=OF,BE=CF,EC=FD,两个正方形的重叠部分的面积始终等于正方形ABCD面积的四分之一等等)
例2、已知,在正方形ABCD中,E是BC的中点,点F在CD上,∠FAE﹦∠BAE.
求证:AF﹦BC+FC.
两种添线方法。
例3、(2006年潍坊市)如图7,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
A. B. C.1- D.1-
【课堂练习】
1.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
A.cm2 B.cm2
C.cm2 D. cm2
2、已知正方形ABCD。
(1)如图1,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H,求证:BE=GH;
(2)如图2,过正方形ABCD内任意一点作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,EF与GH相等吗?请写出你的结论;
(3)当点O在正方形ABCD的边上或外部时,过点O作两条互相垂直的直线,被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗?其中一种情形如图3所示,过正方形ABCD外一点O作互相垂直的两条直线m、n,m与AD、BC的延长线分别交于点E、F,n与AB、DC的延长线分别交于点G、H,试就该图对你的结论加以证明。
练习:
3、现有若干张边长不相等但都大于4cm的正方形纸片,从中任选一张,如图从距离正方形的四个顶点2cm处,沿45°角画线,将正方形纸片分成5部分,则中间阴影部分的面积是 cm;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律? .
【学习体会】
正方形与矩形,菱形,平行四边形的关系如下图。(请填写它们之间的关系)
(2)正方形的性质:
①正方形对边平行。
②正方形四边相等。
③正方形四个角都是直角。
④正方形既是轴对称图形,又是中心对称图形。
⑤正方形对角线相等,互相垂直平分,每条对角线平分一组对
(3)本节课我们把探索和解决问题的思路、方法、结论,从特殊情形逐步推广到一般的情形,从而得到一般的结论,这也是我们获得数学结论的一种重要的思想方法。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
