3.1.3概率的基本性质-高中数学人教A版必修3第三章课件(19张PPT)
文档属性
| 名称 | 3.1.3概率的基本性质-高中数学人教A版必修3第三章课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 825.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 19:03:29 | ||
图片预览






文档简介
3.1.3概率的基本性质
1.上述事件中有必然事件或不可能事件吗?有的话,哪些是?
6. 在掷骰子实验中事件G和事件H是否一定有一个会发生?
5.若只掷一次骰子,则事件C1和事件C2有可能同时发生么?
4.上述事件中,哪些事件发生当且仅当事件D2且事件D3同时发生?
3.上述事件中,哪些事件发生会使得 K={出现1点或5点}也一定发生?
2. 若事件C1发生,则还有哪些事件也一定会发生?
反过来可以么?
探究:课本119页
?
?
?
?
?
?
?
?
不可能
是
?
?
?
?
?
?
?
?
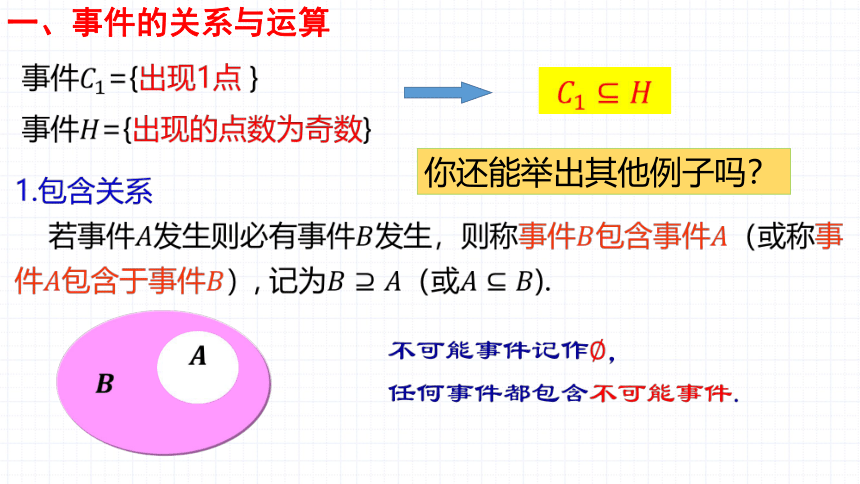
你还能举出其他例子吗?
一、事件的关系与运算
A
B
?
?
?
A
?
你能举出一些例子吗?
B
①
②
③
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
A
B
?
?
?
?
?
?
?
练习:一个人打靶时连续射击两次,事件至少有一次中靶”的互斥事件是( )
D
A.至多有一次中靶
B.两次都中靶
C.只有一次中靶
D.两次都不中靶
?
6.对立事件
若A∩B为不可能事件,A∪B必然事件,那么称事件A与事件B互为对立事件.其含义是:事件A与事件B在任何一次试验中有且仅有一个发生.
练习.从一堆产品(其中正品和次品都多于2件)中任取2件,观察正品件数和次品件数,判断下列每对事件是不是互斥事件,若是,再判断它们是不是对立事件:
(1)恰好有1件次品和恰好有2件次品;
(2)至少有1件次品和全是次品;
(3)至少有1件正品和至少有1件次品;
(4)至少有1件次品和全是正品.
互斥但不对立
不互斥,有包含关系
不互斥,有交叉关系
互斥且不对立
区别:
互斥事件:不同时发生,也可能同时不发生;
对立事件:两个事件不同时发生,但必有一个发生.
对立事件一定是互斥事件
互斥事件不一定是对立事件
如:事件C1与C2是互斥事件,但不是对立事件
互斥事件VS对立事件
二、概率的几个基本性质
(1)对于任何事件的概率的范围是:
必然事件的概率是
不可能事件的概率是
互斥事件的概率加法公式
?
?
?
?
?
用小数或分数表示概率值
?
?
?
?
例1.抛掷一枚均匀的骰子,事件A= “出现点数是奇数”,事件B= “出现点数是偶数”,事件C = “出现点数不超过3”,
求:P(A∪B),P(A∪C).
?
?
二、概率的几个基本性质
?
?
3.如果某士兵射击一次,未中靶的概率为0.05,求中靶概率.
?
?
练习:若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( )
A.0.3 B.0.4 C.0.6 D.0.7
B
1.上述事件中有必然事件或不可能事件吗?有的话,哪些是?
6. 在掷骰子实验中事件G和事件H是否一定有一个会发生?
5.若只掷一次骰子,则事件C1和事件C2有可能同时发生么?
4.上述事件中,哪些事件发生当且仅当事件D2且事件D3同时发生?
3.上述事件中,哪些事件发生会使得 K={出现1点或5点}也一定发生?
2. 若事件C1发生,则还有哪些事件也一定会发生?
反过来可以么?
探究:课本119页
?
?
?
?
?
?
?
?
不可能
是
?
?
?
?
?
?
?
?
你还能举出其他例子吗?
一、事件的关系与运算
A
B
?
?
?
A
?
你能举出一些例子吗?
B
①
②
③
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
A
B
?
?
?
?
?
?
?
练习:一个人打靶时连续射击两次,事件至少有一次中靶”的互斥事件是( )
D
A.至多有一次中靶
B.两次都中靶
C.只有一次中靶
D.两次都不中靶
?
6.对立事件
若A∩B为不可能事件,A∪B必然事件,那么称事件A与事件B互为对立事件.其含义是:事件A与事件B在任何一次试验中有且仅有一个发生.
练习.从一堆产品(其中正品和次品都多于2件)中任取2件,观察正品件数和次品件数,判断下列每对事件是不是互斥事件,若是,再判断它们是不是对立事件:
(1)恰好有1件次品和恰好有2件次品;
(2)至少有1件次品和全是次品;
(3)至少有1件正品和至少有1件次品;
(4)至少有1件次品和全是正品.
互斥但不对立
不互斥,有包含关系
不互斥,有交叉关系
互斥且不对立
区别:
互斥事件:不同时发生,也可能同时不发生;
对立事件:两个事件不同时发生,但必有一个发生.
对立事件一定是互斥事件
互斥事件不一定是对立事件
如:事件C1与C2是互斥事件,但不是对立事件
互斥事件VS对立事件
二、概率的几个基本性质
(1)对于任何事件的概率的范围是:
必然事件的概率是
不可能事件的概率是
互斥事件的概率加法公式
?
?
?
?
?
用小数或分数表示概率值
?
?
?
?
例1.抛掷一枚均匀的骰子,事件A= “出现点数是奇数”,事件B= “出现点数是偶数”,事件C = “出现点数不超过3”,
求:P(A∪B),P(A∪C).
?
?
二、概率的几个基本性质
?
?
3.如果某士兵射击一次,未中靶的概率为0.05,求中靶概率.
?
?
练习:若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( )
A.0.3 B.0.4 C.0.6 D.0.7
B
