4.3.2对数的运算-【新教材】人教A版(2019)高中数学必修第一册课件(16张PPT)
文档属性
| 名称 | 4.3.2对数的运算-【新教材】人教A版(2019)高中数学必修第一册课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 455.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览






文档简介
4.3.2 对数的运算
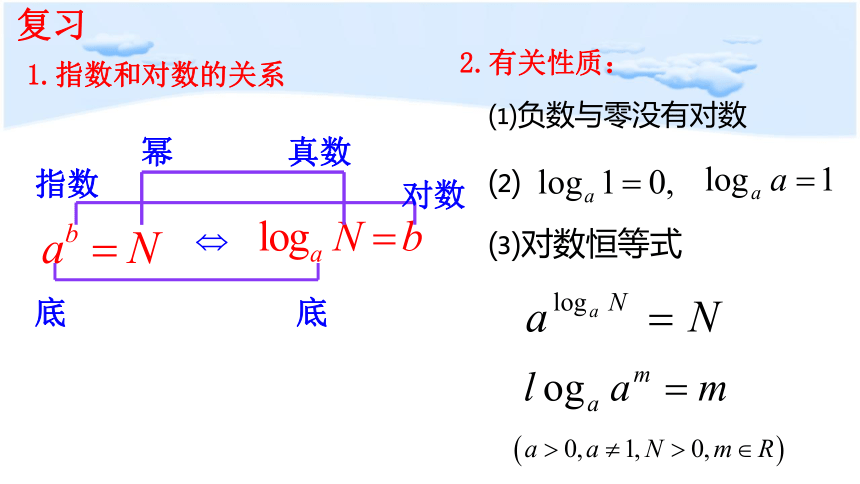
底
底
指数
对数
幂
真数
1.指数和对数的关系
复习
2.有关性质:
⑴负数与零没有对数
⑵
⑶对数恒等式
指数运算法则 :
= ?
+
探究:对数的运算性质
思考1:
化为对数式,
结合指数的运算性质能否将
化为对数式?
将指数式
由
得
由
得
从而得出
思考2:结合前面的推导,由指数式
又能得到什么样的结论?
试一试:由
得
又能得到什么样的结论?
由
得
思考3:由指数式
上述证明是运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式。
①简易语言表达:“积的对数 = 对数的和”…
②有时逆向运用公式
③真数的取值范围必须是
④对公式容易错误记忆,要特别注意:
学习新知
1.用 表示下列各式
解:
例2 求下列各式的值:
(1)
(2)
(2)
解:(1)
(1)
(4)
(3)
(2)
1.求下列各式的值:
【变式练习】
思考4:结合对数的定义,你能推导出对数的换底公式吗?
(a>0,且a≠1; c>0,且c≠1; N>0)
证明:设
由对数的定义可得:
即证得
这个公式叫做换底公式
解:
例.利用对数的换底公式化简下列各式
2011年3月11日,日本东北部海域发生里氏9.0级地震,
它所释放出来的能量是2008年5月12日我国汶川
发生里氏8.0级地震的多少倍(精确到1)?
例.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震M之间的关系为
解:设里氏9.0级和里氏8.0级地震的能量分别为E1和E2
设里利用计算工具可得,
虽然里氏9.0级和里氏8.0级地震仅相差1级,但前者释放出的能量却是后者的约32倍。
例.生物机体内碳14的“半衰期”为5 730年.湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%,试推算马王堆古墓的年代.
死亡年数t
碳14含量P
1
x
2
x2
3
x3
…
…
…
t
xt
解:设生物死亡时,每克组织中的碳14的含量为1,1年后的残留量为x,所以生物体的死亡年数t与其体内每克组织的碳14含量P有如下关系:
因此,生物死亡t年后体内碳14的含量
…
1.用 表示下列各式:
练习
解:
点评:牢记对数的运算法则,直接利用公式.
2.计算
1.对数的运算法则;
2.利用定义及指数运算证明
对数的运算法则;
3.对数运算法则的应用;
4.换底公式的证明及应用.
积、商、幂的对数运算法则:
如果a>0,且a?1,M>0,N>0,那么:
(c>0,且c≠1)
底
底
指数
对数
幂
真数
1.指数和对数的关系
复习
2.有关性质:
⑴负数与零没有对数
⑵
⑶对数恒等式
指数运算法则 :
= ?
+
探究:对数的运算性质
思考1:
化为对数式,
结合指数的运算性质能否将
化为对数式?
将指数式
由
得
由
得
从而得出
思考2:结合前面的推导,由指数式
又能得到什么样的结论?
试一试:由
得
又能得到什么样的结论?
由
得
思考3:由指数式
上述证明是运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式。
①简易语言表达:“积的对数 = 对数的和”…
②有时逆向运用公式
③真数的取值范围必须是
④对公式容易错误记忆,要特别注意:
学习新知
1.用 表示下列各式
解:
例2 求下列各式的值:
(1)
(2)
(2)
解:(1)
(1)
(4)
(3)
(2)
1.求下列各式的值:
【变式练习】
思考4:结合对数的定义,你能推导出对数的换底公式吗?
(a>0,且a≠1; c>0,且c≠1; N>0)
证明:设
由对数的定义可得:
即证得
这个公式叫做换底公式
解:
例.利用对数的换底公式化简下列各式
2011年3月11日,日本东北部海域发生里氏9.0级地震,
它所释放出来的能量是2008年5月12日我国汶川
发生里氏8.0级地震的多少倍(精确到1)?
例.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震M之间的关系为
解:设里氏9.0级和里氏8.0级地震的能量分别为E1和E2
设里利用计算工具可得,
虽然里氏9.0级和里氏8.0级地震仅相差1级,但前者释放出的能量却是后者的约32倍。
例.生物机体内碳14的“半衰期”为5 730年.湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%,试推算马王堆古墓的年代.
死亡年数t
碳14含量P
1
x
2
x2
3
x3
…
…
…
t
xt
解:设生物死亡时,每克组织中的碳14的含量为1,1年后的残留量为x,所以生物体的死亡年数t与其体内每克组织的碳14含量P有如下关系:
因此,生物死亡t年后体内碳14的含量
…
1.用 表示下列各式:
练习
解:
点评:牢记对数的运算法则,直接利用公式.
2.计算
1.对数的运算法则;
2.利用定义及指数运算证明
对数的运算法则;
3.对数运算法则的应用;
4.换底公式的证明及应用.
积、商、幂的对数运算法则:
如果a>0,且a?1,M>0,N>0,那么:
(c>0,且c≠1)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
