第13章全等三角形的性质和判定的综合运用-华东师大版八年级数学上册复习讲义(含答案)
文档属性
| 名称 | 第13章全等三角形的性质和判定的综合运用-华东师大版八年级数学上册复习讲义(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 08:21:21 | ||
图片预览



文档简介
全等三角形的性质和判定的综合运用
1、全等三角形的概念及其性质
(1)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
(2)全等三角形性质: (1)对应边相等 (2)对应角相等 (3)周长相等 (4)面积相等
特别提醒:找准两个全等三角形的对应边和对应角是证明三角形全等的关键,要学会找对应角、对应边。
例1.如图,△ABD≌△EBC,AB=3cm,BC=6cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
例2. 如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.
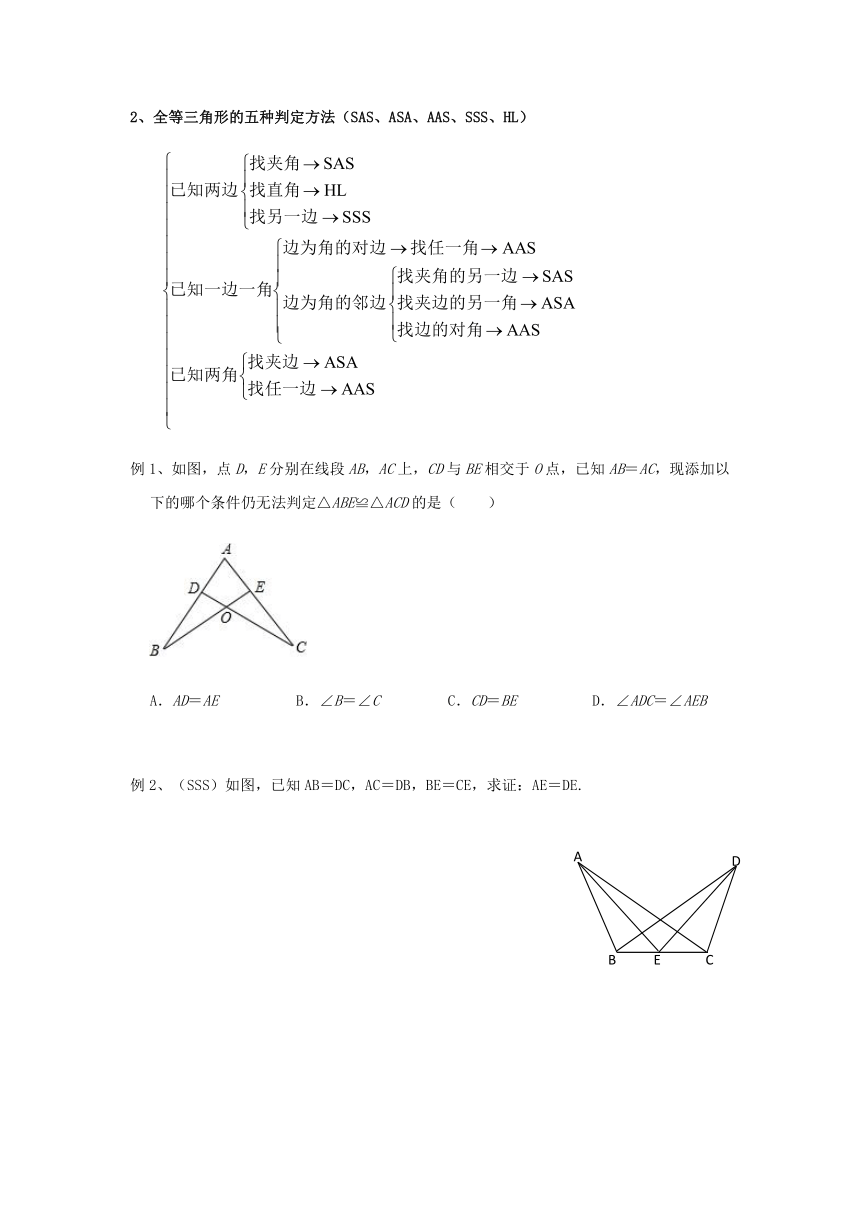
全等三角形的五种判定方法(SAS、ASA、AAS、SSS、HL)
false
例1、如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
例2、(SSS)如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.
3806825224155A
B
E
C
D
A
B
E
C
D
例3、(AAS)如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)△AEC与△CFB全等吗?请说明理由;
(2)请说明BF,AE,EF之间的数量关系.
例4、(SAS)已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF,求证:△ABC≌△DEF.
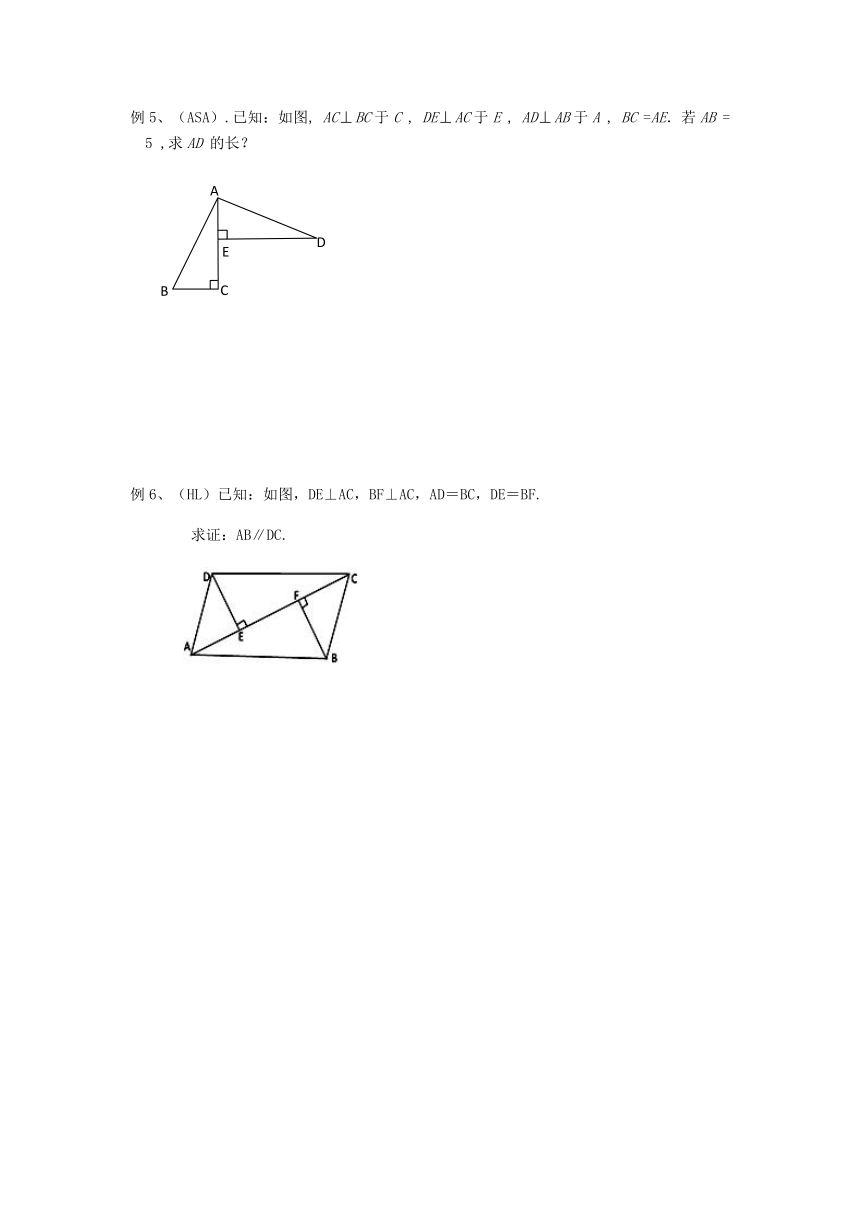
例5、(ASA).已知:如图, ACfalseBC于C , DEfalseAC于E , ADfalseAB于A , BC =AE.若AB = 5 ,求AD 的长?
D
C
B
A
E
D
C
B
A
E
例6、(HL)已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
求证:AB∥DC.
3、综合练习:
1、如图,已知点C是线段BD上一点,以BC、DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD,BE相交于点F,AC和BE交于点M,AD,CE交于点N,(注:等边三角形的每一个内角都等于60°)
(1)求证:AD=BE
(2)线段CM与CN相等吗?请证明你的结论.
(3)求∠BFD的度数.
2、如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
3、小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
4、如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.求证:(1)∠B=∠D;(2)△ABC≌△ADE.
5、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
6、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
A
E
B
M
C
F
A
E
B
M
C
F
7、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
全等三角形的性质和判定的综合运用
1、全等三角形的概念及其性质
(1)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
(2)全等三角形性质: (1)对应边相等 (2)对应角相等 (3)周长相等 (4)面积相等
特别提醒:找准两个全等三角形的对应边和对应角是证明三角形全等的关键,要学会找对应角、对应边。
例1.如图,△ABD≌△EBC,AB=3cm,BC=6cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
解:(1)∵△ABD≌△EBC,
∴BD=BC=6cm,BE=AB=3cm,
∴DE=BD﹣BE=3cm;
(2)DB⊥AC.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又∵∠ABD+∠EBC=180°,
∴∠ABD=∠EBC=90°,
∴DB⊥AC.
例2. 如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.
解∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28,∠2=5,∠3=3,
∴28+5+3=36=180°,=5°
即∠1=140°,∠2=25°,∠3=15°
∵△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,
∴△ABE≌△ADC≌△ABC
∴∠2=∠ABE,∠3=∠ACD
∴∠α=∠EBC+∠BCD=2∠2+2∠3=50°+30°=80°
全等三角形的五种判定方法(SAS、ASA、AAS、SSS、HL)
false
例1、如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
解:∵AB=AC,∠BAE=∠CAD,
∴当添加AE=AD时,可根据“SAS”判断△ABE≌△ACD;
当添加∠B=∠C时,可根据“ASA”判断△ABE≌△ACD;
当添加∠AEB=∠ADC时,可根据“AAS”判断△ABE≌△ACD.
故选:C.
例2、(SSS)如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.
证明:∵AB=DC,AC=DB,BC=BC
290893535560A
B
E
C
D
A
B
E
C
D
∴△ABC≌△DCB,
∴∠ABC=∠DCB
又∵BE=CE,AB=DC
∴△ABE≌△DCE
∴AE=DE
例3、(AAS)如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)△AEC与△CFB全等吗?请说明理由;
(2)请说明BF,AE,EF之间的数量关系.
解:(1)全等,理由如下:
在△ABC中,∠ACB=90°,
∴∠ACE+∠BCF=90°,
又∵BF⊥CE于F,
∴∠CBF+∠BCF=90°.
∴∠ACE=∠CBF.
在△ACE与△CBF中,
∠E=∠BFC∠ACE=∠FBCAC=BC,
∴△ACE≌△CBF (AAS);
(2)BF=EF+AE,理由如下:
由(1)知:△AEC≌△CFB,
∴AE=CF,EC=BF,
又∵EC=EF+CF,
∴EC=EF+AE.
∴EC=BF=EF+AE,
∴BF=EF+AE.
例4、(SAS)已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF,求证:△ABC≌△DEF.
证明:∵BF=CE
∴BF+FC=CE+FC
∴BC=FE
∵AC∥DF
∴∠ACB=∠DFE,
在△ABC和△DEF中,
false,
∴△ABC≌△DEF(SAS).
例5、(ASA).已知:如图, ACfalseBC于C , DEfalseAC于E , ADfalseAB于A , BC =AE.若AB = 5 ,求AD 的长?
D
C
B
A
E
D
C
B
A
E
解:∵AD⊥AB
∴∠BAC=∠ADE
又∵AC⊥BC于C,DE⊥AC于E
根据三角形角度之和等于180度
∴∠ABC=∠DAE
∵BC=AE,△ABC≌△DAE(ASA)
∴AD=AB=5
例6、(HL)已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
求证:AB∥DC.
证明:∵DE⊥AC,BF⊥AC,
∴在Rt△ADE与Rt△CBF中
∴Rt△ADE≌Rt△CBF (HL)
∴AE=CF,DE=BF
∴AE+EF=CF+EF,即AF=CE
在Rt△CDE与Rt△ABF中,
∴Rt△CDE≌Rt△ABF(SAS)
∴∠DCE=∠BAF
∴AB∥DC.
3、综合练习:
1、如图,已知点C是线段BD上一点,以BC、DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD,BE相交于点F,AC和BE交于点M,AD,CE交于点N,(注:等边三角形的每一个内角都等于60°)
(1)求证:AD=BE
(2)线段CM与CN相等吗?请证明你的结论.
(3)求∠BFD的度数.
(1)证明:∵△ABC是等边三角形,
∴BC=AC,∠BAC=∠ABC=∠ACB=60°,
同理:CE=CD,∠ECD=60°,
∴∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△ACD和△BCE中,AC=BC∠ACD=∠BCECD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解;CM=CN,理由如下:
∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠ACB=∠ECD=60°,
∴∠ACE=60°
∴∠ACB=∠ACE,
在△BCM和△ACN中,∠CBM=∠CANBC=AC∠BCM=∠ACN,
∴△BCM≌△ACN(ASA),
∴CM=CN;
(3)解:∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∴∠BFD=∠BAF+∠ABE=∠BAC+∠CAD+∠ABE=∠BAC+∠CBE+∠ABE=∠BAC+∠ABC=60°+60°=120°.
2、如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
证明:(1)因为∠A=∠D=90°,所以△ABC和△DCB都是直角三角形,
在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形. 理由如下:
∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DCB,
∴OB=OC
∴△OBC是等腰三角形.
3、小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
4、如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.求证:(1)∠B=∠D;(2)△ABC≌△ADE.
证明:(1)∵∠1=∠3,
∴∠1+∠DAC=∠3+∠DAC,
即∠BAC=∠DAE,
∵∠E=∠180°﹣∠3﹣∠ACE,∠ACB=180°﹣∠2﹣∠ACE,
∵∠2=∠3,∠ACE=∠ACE,
∴∠ACB=∠E,
在△ABC与△ADE中
,
∴△ABC≌△ADE(ASA),
∴∠B=∠D.
(2)由(1)可得△ABC≌△ADE.
5、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
证明:
(1)
∵BE⊥AC,CF⊥AB
∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°
∴∠ABM=∠ACN
∵BM=AC,CN=AB
∴△ABM≌△NAC
∴AM=AN
(2)
∵△ABM≌△NAC
∴∠BAM=∠N
∵∠N+∠BAN=90°
∴∠BAM+∠BAN=90°
即∠MAN=90°
∴AM⊥AN
6、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
A
E
B
M
C
F
A
E
B
M
C
F
(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵AE=AB,∠EAC=∠BAF,AF=AC,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,
∴EC⊥BF.
7、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
(1)证明:连接BE,DF.
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEC=∠BFA=90°,DE∥BF,
在Rt△DEC和Rt△BFA中,
∵AF=CE,AB=CD,
∴Rt△DEC≌Rt△BFA(HL),
∴DE=BF.
∴四边形BEDF是平行四边形.
∴MB=MD,ME=MF;
(2)解:连接BE,DF.
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEC=∠BFA=90°,DE∥BF,
在Rt△DEC和Rt△BFA中,
∵AF=CE,AB=CD,
∴Rt△DEC≌Rt△BFA(HL),
∴DE=BF.
∴四边形BEDF是平行四边形.
∴MB=MD,ME=MF.
1、全等三角形的概念及其性质
(1)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
(2)全等三角形性质: (1)对应边相等 (2)对应角相等 (3)周长相等 (4)面积相等
特别提醒:找准两个全等三角形的对应边和对应角是证明三角形全等的关键,要学会找对应角、对应边。
例1.如图,△ABD≌△EBC,AB=3cm,BC=6cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
例2. 如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.
全等三角形的五种判定方法(SAS、ASA、AAS、SSS、HL)
false
例1、如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
例2、(SSS)如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.
3806825224155A
B
E
C
D
A
B
E
C
D
例3、(AAS)如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)△AEC与△CFB全等吗?请说明理由;
(2)请说明BF,AE,EF之间的数量关系.
例4、(SAS)已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF,求证:△ABC≌△DEF.
例5、(ASA).已知:如图, ACfalseBC于C , DEfalseAC于E , ADfalseAB于A , BC =AE.若AB = 5 ,求AD 的长?
D
C
B
A
E
D
C
B
A
E
例6、(HL)已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
求证:AB∥DC.
3、综合练习:
1、如图,已知点C是线段BD上一点,以BC、DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD,BE相交于点F,AC和BE交于点M,AD,CE交于点N,(注:等边三角形的每一个内角都等于60°)
(1)求证:AD=BE
(2)线段CM与CN相等吗?请证明你的结论.
(3)求∠BFD的度数.
2、如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
3、小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
4、如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.求证:(1)∠B=∠D;(2)△ABC≌△ADE.
5、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
6、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
A
E
B
M
C
F
A
E
B
M
C
F
7、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
全等三角形的性质和判定的综合运用
1、全等三角形的概念及其性质
(1)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
(2)全等三角形性质: (1)对应边相等 (2)对应角相等 (3)周长相等 (4)面积相等
特别提醒:找准两个全等三角形的对应边和对应角是证明三角形全等的关键,要学会找对应角、对应边。
例1.如图,△ABD≌△EBC,AB=3cm,BC=6cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
解:(1)∵△ABD≌△EBC,
∴BD=BC=6cm,BE=AB=3cm,
∴DE=BD﹣BE=3cm;
(2)DB⊥AC.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又∵∠ABD+∠EBC=180°,
∴∠ABD=∠EBC=90°,
∴DB⊥AC.
例2. 如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.
解∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28,∠2=5,∠3=3,
∴28+5+3=36=180°,=5°
即∠1=140°,∠2=25°,∠3=15°
∵△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,
∴△ABE≌△ADC≌△ABC
∴∠2=∠ABE,∠3=∠ACD
∴∠α=∠EBC+∠BCD=2∠2+2∠3=50°+30°=80°
全等三角形的五种判定方法(SAS、ASA、AAS、SSS、HL)
false
例1、如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
解:∵AB=AC,∠BAE=∠CAD,
∴当添加AE=AD时,可根据“SAS”判断△ABE≌△ACD;
当添加∠B=∠C时,可根据“ASA”判断△ABE≌△ACD;
当添加∠AEB=∠ADC时,可根据“AAS”判断△ABE≌△ACD.
故选:C.
例2、(SSS)如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.
证明:∵AB=DC,AC=DB,BC=BC
290893535560A
B
E
C
D
A
B
E
C
D
∴△ABC≌△DCB,
∴∠ABC=∠DCB
又∵BE=CE,AB=DC
∴△ABE≌△DCE
∴AE=DE
例3、(AAS)如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)△AEC与△CFB全等吗?请说明理由;
(2)请说明BF,AE,EF之间的数量关系.
解:(1)全等,理由如下:
在△ABC中,∠ACB=90°,
∴∠ACE+∠BCF=90°,
又∵BF⊥CE于F,
∴∠CBF+∠BCF=90°.
∴∠ACE=∠CBF.
在△ACE与△CBF中,
∠E=∠BFC∠ACE=∠FBCAC=BC,
∴△ACE≌△CBF (AAS);
(2)BF=EF+AE,理由如下:
由(1)知:△AEC≌△CFB,
∴AE=CF,EC=BF,
又∵EC=EF+CF,
∴EC=EF+AE.
∴EC=BF=EF+AE,
∴BF=EF+AE.
例4、(SAS)已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF,求证:△ABC≌△DEF.
证明:∵BF=CE
∴BF+FC=CE+FC
∴BC=FE
∵AC∥DF
∴∠ACB=∠DFE,
在△ABC和△DEF中,
false,
∴△ABC≌△DEF(SAS).
例5、(ASA).已知:如图, ACfalseBC于C , DEfalseAC于E , ADfalseAB于A , BC =AE.若AB = 5 ,求AD 的长?
D
C
B
A
E
D
C
B
A
E
解:∵AD⊥AB
∴∠BAC=∠ADE
又∵AC⊥BC于C,DE⊥AC于E
根据三角形角度之和等于180度
∴∠ABC=∠DAE
∵BC=AE,△ABC≌△DAE(ASA)
∴AD=AB=5
例6、(HL)已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
求证:AB∥DC.
证明:∵DE⊥AC,BF⊥AC,
∴在Rt△ADE与Rt△CBF中
∴Rt△ADE≌Rt△CBF (HL)
∴AE=CF,DE=BF
∴AE+EF=CF+EF,即AF=CE
在Rt△CDE与Rt△ABF中,
∴Rt△CDE≌Rt△ABF(SAS)
∴∠DCE=∠BAF
∴AB∥DC.
3、综合练习:
1、如图,已知点C是线段BD上一点,以BC、DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD,BE相交于点F,AC和BE交于点M,AD,CE交于点N,(注:等边三角形的每一个内角都等于60°)
(1)求证:AD=BE
(2)线段CM与CN相等吗?请证明你的结论.
(3)求∠BFD的度数.
(1)证明:∵△ABC是等边三角形,
∴BC=AC,∠BAC=∠ABC=∠ACB=60°,
同理:CE=CD,∠ECD=60°,
∴∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
在△ACD和△BCE中,AC=BC∠ACD=∠BCECD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解;CM=CN,理由如下:
∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠ACB=∠ECD=60°,
∴∠ACE=60°
∴∠ACB=∠ACE,
在△BCM和△ACN中,∠CBM=∠CANBC=AC∠BCM=∠ACN,
∴△BCM≌△ACN(ASA),
∴CM=CN;
(3)解:∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∴∠BFD=∠BAF+∠ABE=∠BAC+∠CAD+∠ABE=∠BAC+∠CBE+∠ABE=∠BAC+∠ABC=60°+60°=120°.
2、如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
证明:(1)因为∠A=∠D=90°,所以△ABC和△DCB都是直角三角形,
在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形. 理由如下:
∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DCB,
∴OB=OC
∴△OBC是等腰三角形.
3、小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36﹣10=26(m),
答:楼高AB是26米.
4、如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.求证:(1)∠B=∠D;(2)△ABC≌△ADE.
证明:(1)∵∠1=∠3,
∴∠1+∠DAC=∠3+∠DAC,
即∠BAC=∠DAE,
∵∠E=∠180°﹣∠3﹣∠ACE,∠ACB=180°﹣∠2﹣∠ACE,
∵∠2=∠3,∠ACE=∠ACE,
∴∠ACB=∠E,
在△ABC与△ADE中
,
∴△ABC≌△ADE(ASA),
∴∠B=∠D.
(2)由(1)可得△ABC≌△ADE.
5、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
证明:
(1)
∵BE⊥AC,CF⊥AB
∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°
∴∠ABM=∠ACN
∵BM=AC,CN=AB
∴△ABM≌△NAC
∴AM=AN
(2)
∵△ABM≌△NAC
∴∠BAM=∠N
∵∠N+∠BAN=90°
∴∠BAM+∠BAN=90°
即∠MAN=90°
∴AM⊥AN
6、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
A
E
B
M
C
F
A
E
B
M
C
F
(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵AE=AB,∠EAC=∠BAF,AF=AC,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,
∴EC⊥BF.
7、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
(1)证明:连接BE,DF.
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEC=∠BFA=90°,DE∥BF,
在Rt△DEC和Rt△BFA中,
∵AF=CE,AB=CD,
∴Rt△DEC≌Rt△BFA(HL),
∴DE=BF.
∴四边形BEDF是平行四边形.
∴MB=MD,ME=MF;
(2)解:连接BE,DF.
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEC=∠BFA=90°,DE∥BF,
在Rt△DEC和Rt△BFA中,
∵AF=CE,AB=CD,
∴Rt△DEC≌Rt△BFA(HL),
∴DE=BF.
∴四边形BEDF是平行四边形.
∴MB=MD,ME=MF.
