第13章等腰三角形-华东师大版八年级数学上册复习讲义(含答案)
文档属性
| 名称 | 第13章等腰三角形-华东师大版八年级数学上册复习讲义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览



文档简介
等腰三角形
【知识梳理】
一、等腰三角形
1.等腰三角形的有关概念及分类
有两边相等的三角形叫做等腰三角形,三边相等的三角形叫做等边三角形,也叫做正三角形;等腰三角形分为腰和底 的等腰三角形和______三角形.
2.等腰三角形的性质
(1)等腰三角形的两个底角相等(简称为“等边对等角”);
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);
(3)等腰三角形是轴对称图形.
3.等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”).
二、等边三角形的性质与判定
1.等边三角形的性质
(1)等边三角形的内角相等,且都等于________;(2)等边三角形的三条边都________.
2.等边三角形的判定
(1)________相等的三角形是等边三角形;
(2)________相等的三角形是等边三角形;
(3)有一个角为________的等腰三角形是等边三角形.
三、线段的垂直平分线
1.概念:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫________.
2.性质:线段垂直平分线上的点到这条线段两个端点的距离________.
3.判定:到一条线段的两个端点__________的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.
四、角的平分线
1.性质:角平分线上的点到角的两边的距离________.
2.判定:角的内部到角的两边距离相等的点在角的______上,角的平分线可以看作是到角的两边距离相等的点的集合.
五、含30°的直角三角形 直角三角形中30°所对的边是斜边的一半
板块一、等腰三角形的性质与判定
例1、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( ).
A.60° B.120° C.60°或150° D.60°或120°
例2、如图,在△ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.
例3、已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:(1)△ABD≌△CFD;(2)BE⊥AC.
例4、如右图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:(1)BC=AD; (2)△OAB是等腰三角形.
523240137795
板块二、等边三角形的性质与判定
如图,已知点B、C、D在同一条直线上,和都是等边三角形,BE交AC于F,
AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)求证:FH∥BD.
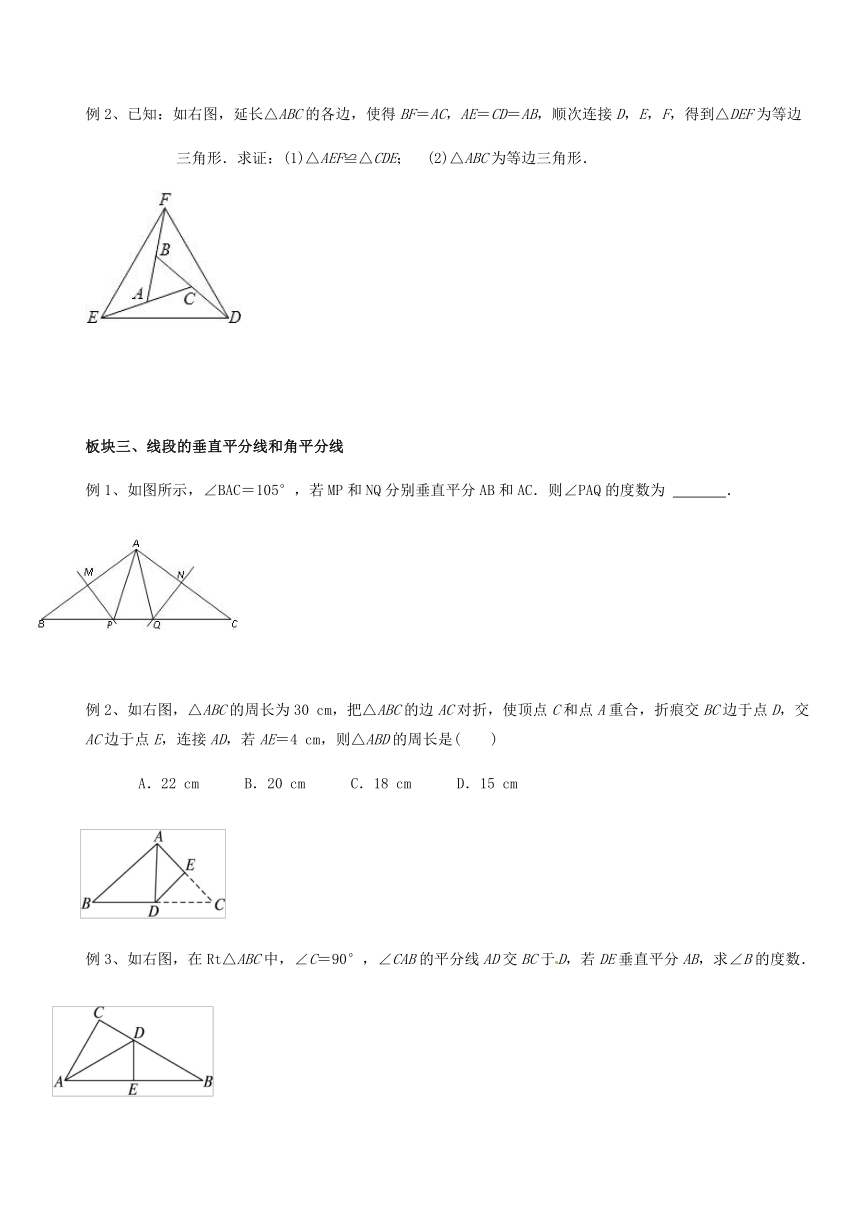
例2、已知:如右图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边
三角形.求证:(1)△AEF≌△CDE; (2)△ABC为等边三角形.
板块三、线段的垂直平分线和角平分线
如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.则∠PAQ的度数为 .
-85725097155
例2、如右图,△ABC的周长为30 cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4 cm,则△ABD的周长是( )
A.22 cm B.20 cm C.18 cm D.15 cm
708025114935
例3、如右图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
465455122555
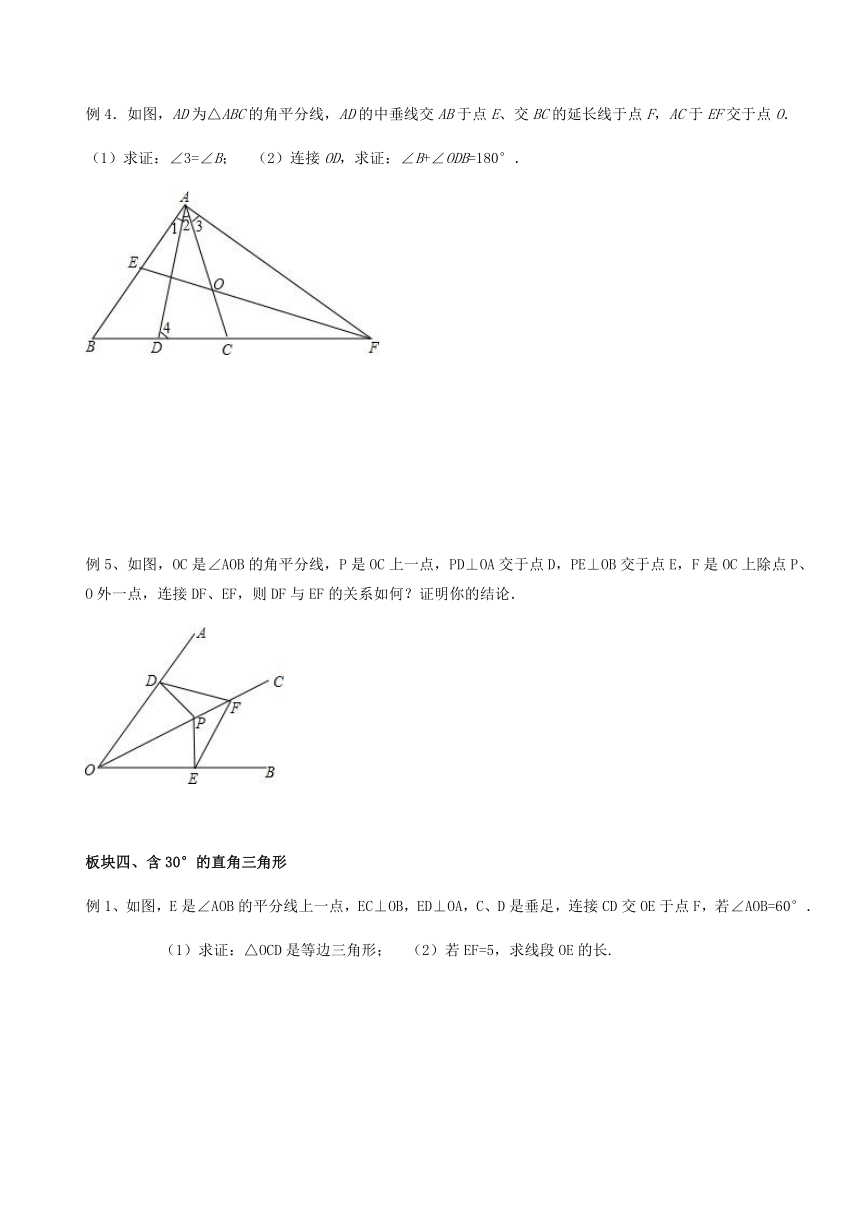
例4.如图,AD为△ABC的角平分线,AD的中垂线交AB于点E、交BC的延长线于点F,AC于EF交于点O.
(1)求证:∠3=∠B; (2)连接OD,求证:∠B+∠ODB=180°.
例5、如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交于点D,PE⊥OB交于点E,F是OC上除点P、O外一点,连接DF、EF,则DF与EF的关系如何?证明你的结论.
板块四、含30°的直角三角形
例1、如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.
求证:△OCD是等边三角形; (2)若EF=5,求线段OE的长.
例2、如图所示,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于点H,HD=1,HE=2,试求BD和CE的长.
等腰三角形
【知识梳理】
一、等腰三角形
1.等腰三角形的有关概念及分类
有两边相等的三角形叫做等腰三角形,三边相等的三角形叫做等边三角形,也叫做正三角形;等腰三角形分为腰和底 的等腰三角形和______三角形.
2.等腰三角形的性质
(1)等腰三角形的两个底角相等(简称为“等边对等角”);
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);
(3)等腰三角形是轴对称图形.
3.等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”).
二、等边三角形的性质与判定
1.等边三角形的性质
(1)等边三角形的内角相等,且都等于________;(2)等边三角形的三条边都________.
2.等边三角形的判定
(1)________相等的三角形是等边三角形;
(2)________相等的三角形是等边三角形;
(3)有一个角为________的等腰三角形是等边三角形.
三、线段的垂直平分线
1.概念:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫________.
2.性质:线段垂直平分线上的点到这条线段两个端点的距离________.
3.判定:到一条线段的两个端点__________的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.
四、角的平分线
1.性质:角平分线上的点到角的两边的距离________.
2.判定:角的内部到角的两边距离相等的点在角的______上,角的平分线可以看作是到角的两边距离相等的点的集合.
五、含30°的直角三角形 直角三角形中30°所对的边是斜边的一半
板块一、等腰三角形的性质与判定
例1、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( D ).
A.60° B.120° C.60°或150° D.60°或120°
例2、如图,在△ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.
解:AB=AC=BD,
∴∠B=∠C,∠2=∠3.
设∠2=x°=∠BAD,
∠B=∠C=180°-2x,
由三角形外角的性质得∠2=∠1+∠C,
即x=30°+(180°-2x)
解得x=70°,
则∠2=70°.
例3、已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:(1)△ABD≌△CFD;(2)BE⊥AC.
证明:(1) ∵ AD⊥BC,∴ ∠ADC=∠FDB=90°.
∵ ,
∴
∴ AD=CD
∵ ,
∴ △ABD≌△CFD
(2)∵△ABD≌△CFD
∴ BD=FD.
∵ ∠FDB=90°,
∴ .
∵ ,
∴ .
∴ BE⊥AC.
例4、如右图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:(1)BC=AD; (2)△OAB是等腰三角形.
523240137795
证明:(1)∵AC ⊥BC ,BD ⊥AD??????
∴?∠D= ∠C=90°???
在Rt△ACB和Rt △BDA中,AB= BA,AC=BD ,??
∴△ACB≌△BDA(HL)????
∴BC=AD;
(2)由△ACB≌?△BDA 得∠C AB=∠D BA?????????????
?∴△OAB是等腰三角形
板块二、等边三角形的性质与判定
如图,已知点B、C、D在同一条直线上,和都是等边三角形,BE交AC于F,
AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)求证:FH∥BD.
(1)证明:和都是等边三角形
∴BC=AC,CE=CD,∠BCA=∠ECD=60°
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD
在△BCE和△ACD中
false
∴△BCE≌△ACD(SAS)
(2)由(1)知△BCE≌△ACD
则∠CBF=∠CAH,BC=AC
又∵和都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF,
在△BCF和△ACH中
false
∴△BCF≌△ACH(ASA)
∴CF=CH,
又∵∠FCH=60°
∴△CHF是等边三角形
∴∠FHC=∠HCD=60°,
∴FH∥BD
例2、已知:如右图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边
三角形.求证:(1)△AEF≌△CDE; (2)△ABC为等边三角形.
证明:(1)∵BF=AC,AB=AE,
∴FA=EC,
∵△DEF是等边三角形,
∴EF=DE,
又∵AE=CD(已知),
∴△AEF≌△CDE(SSS);
(2)由△AEF≌△CDE,得∠FEA=∠EDC,
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
△DEF是等边三角形,
∴∠DEF=60°,
∴∠BCA=60°,同理可得∠BAC=60°,
∴△ABC中,AB=BC,
∴△ABC是等边三角形。
板块三、线段的垂直平分线和角平分线
如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.则∠PAQ的度数为 30° .
-85725097155
例2、如右图,△ABC的周长为30 cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4 cm,则△ABD的周长是( A )
A.22 cm B.20 cm C.18 cm D.15 cm
708025114935
例3、如右图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
465455122555
解:∵在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,
∴∠DAE=?∠CAB=(90°-∠B),
∵DE垂直平分AB,
∴AD=BD,
∴∠DAE=∠B,
∴∠DAE=?∠CAB=?(90°-∠B)=∠B,
∴3∠B=90°,
∴∠B=30°.
例4.如图,AD为△ABC的角平分线,AD的中垂线交AB于点E、交BC的延长线于点F,AC于EF交于点O.
(1)求证:∠3=∠B; (2)连接OD,求证:∠B+∠ODB=180°.
证明:(1)∵AD为△ABC的角平分线,
∴∠1=∠2,
∵AD的中垂线交AB于点E、BC的延长线于点F,
∴AF=DF,
∴∠4=∠DAF=∠2+∠3,
∵∠4=∠1+∠B,
∴∠3=∠B;
(2)∵EF是AD的中垂线,
∴OA=OD,
∴∠2=∠ODA,
∵∠4=∠DAF,
∴∠3=∠ODF,
∵∠3=∠B,
∴∠ODF=∠B,
∴OD∥AB,
∴∠B+∠ODB=180°.
例5、如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交于点D,PE⊥OB交于点E,F是OC上除点P、O外一点,连接DF、EF,则DF与EF的关系如何?证明你的结论.
解:DF=EF.
理由如下:
∵OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交于点D,PE⊥OB交于点E,
∴PD=PE,
由HL定理易证△OPD≌△OPE,
∴∠OPD=∠OPE,∴∠DPF=∠EPF.
在△DPF与△EPF中,
,
∴△DPF≌△EPF,
∴DF=EF.
板块四、含30°的直角三角形
例1、如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.
求证:△OCD是等边三角形; (2)若EF=5,求线段OE的长.
解:(1)∵点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,
∴DE=CE,
在Rt△ODE和Rt△OCE中,
false
∴Rt△ODE≌Rt△OCE(LH)
∴OD=OC,
∵∠AOB=60°,
∴△OCD是等边三角形;
(2)∵△OCD是等边三角形,OF是角平分线,
∴OE⊥DC,
∵∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵∠ODF=60°,ED⊥OA,
∴∠EDF=30°,
∴DE=2EF=10,
∴OE=2DE=20.
例2、如图所示,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于点H,HD=1,HE=2,试求BD和CE的长.
解:∵BD⊥AC于D,∠A=60°,
∴∠ABD=90°-60°=30°,
在Rt△BEH中,∠HEB=90°,∠EBH=30°.
∴BH=2EH=4.
同理可得,CH=2HD=2,
∴BD=BH+HD=4+1=5.
CE=CH+HE=2+2=4.
【知识梳理】
一、等腰三角形
1.等腰三角形的有关概念及分类
有两边相等的三角形叫做等腰三角形,三边相等的三角形叫做等边三角形,也叫做正三角形;等腰三角形分为腰和底 的等腰三角形和______三角形.
2.等腰三角形的性质
(1)等腰三角形的两个底角相等(简称为“等边对等角”);
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);
(3)等腰三角形是轴对称图形.
3.等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”).
二、等边三角形的性质与判定
1.等边三角形的性质
(1)等边三角形的内角相等,且都等于________;(2)等边三角形的三条边都________.
2.等边三角形的判定
(1)________相等的三角形是等边三角形;
(2)________相等的三角形是等边三角形;
(3)有一个角为________的等腰三角形是等边三角形.
三、线段的垂直平分线
1.概念:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫________.
2.性质:线段垂直平分线上的点到这条线段两个端点的距离________.
3.判定:到一条线段的两个端点__________的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.
四、角的平分线
1.性质:角平分线上的点到角的两边的距离________.
2.判定:角的内部到角的两边距离相等的点在角的______上,角的平分线可以看作是到角的两边距离相等的点的集合.
五、含30°的直角三角形 直角三角形中30°所对的边是斜边的一半
板块一、等腰三角形的性质与判定
例1、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( ).
A.60° B.120° C.60°或150° D.60°或120°
例2、如图,在△ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.
例3、已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:(1)△ABD≌△CFD;(2)BE⊥AC.
例4、如右图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:(1)BC=AD; (2)△OAB是等腰三角形.
523240137795
板块二、等边三角形的性质与判定
如图,已知点B、C、D在同一条直线上,和都是等边三角形,BE交AC于F,
AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)求证:FH∥BD.
例2、已知:如右图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边
三角形.求证:(1)△AEF≌△CDE; (2)△ABC为等边三角形.
板块三、线段的垂直平分线和角平分线
如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.则∠PAQ的度数为 .
-85725097155
例2、如右图,△ABC的周长为30 cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4 cm,则△ABD的周长是( )
A.22 cm B.20 cm C.18 cm D.15 cm
708025114935
例3、如右图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
465455122555
例4.如图,AD为△ABC的角平分线,AD的中垂线交AB于点E、交BC的延长线于点F,AC于EF交于点O.
(1)求证:∠3=∠B; (2)连接OD,求证:∠B+∠ODB=180°.
例5、如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交于点D,PE⊥OB交于点E,F是OC上除点P、O外一点,连接DF、EF,则DF与EF的关系如何?证明你的结论.
板块四、含30°的直角三角形
例1、如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.
求证:△OCD是等边三角形; (2)若EF=5,求线段OE的长.
例2、如图所示,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于点H,HD=1,HE=2,试求BD和CE的长.
等腰三角形
【知识梳理】
一、等腰三角形
1.等腰三角形的有关概念及分类
有两边相等的三角形叫做等腰三角形,三边相等的三角形叫做等边三角形,也叫做正三角形;等腰三角形分为腰和底 的等腰三角形和______三角形.
2.等腰三角形的性质
(1)等腰三角形的两个底角相等(简称为“等边对等角”);
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);
(3)等腰三角形是轴对称图形.
3.等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称为“等角对等边”).
二、等边三角形的性质与判定
1.等边三角形的性质
(1)等边三角形的内角相等,且都等于________;(2)等边三角形的三条边都________.
2.等边三角形的判定
(1)________相等的三角形是等边三角形;
(2)________相等的三角形是等边三角形;
(3)有一个角为________的等腰三角形是等边三角形.
三、线段的垂直平分线
1.概念:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫________.
2.性质:线段垂直平分线上的点到这条线段两个端点的距离________.
3.判定:到一条线段的两个端点__________的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.
四、角的平分线
1.性质:角平分线上的点到角的两边的距离________.
2.判定:角的内部到角的两边距离相等的点在角的______上,角的平分线可以看作是到角的两边距离相等的点的集合.
五、含30°的直角三角形 直角三角形中30°所对的边是斜边的一半
板块一、等腰三角形的性质与判定
例1、等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( D ).
A.60° B.120° C.60°或150° D.60°或120°
例2、如图,在△ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.
解:AB=AC=BD,
∴∠B=∠C,∠2=∠3.
设∠2=x°=∠BAD,
∠B=∠C=180°-2x,
由三角形外角的性质得∠2=∠1+∠C,
即x=30°+(180°-2x)
解得x=70°,
则∠2=70°.
例3、已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:(1)△ABD≌△CFD;(2)BE⊥AC.
证明:(1) ∵ AD⊥BC,∴ ∠ADC=∠FDB=90°.
∵ ,
∴
∴ AD=CD
∵ ,
∴ △ABD≌△CFD
(2)∵△ABD≌△CFD
∴ BD=FD.
∵ ∠FDB=90°,
∴ .
∵ ,
∴ .
∴ BE⊥AC.
例4、如右图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:(1)BC=AD; (2)△OAB是等腰三角形.
523240137795
证明:(1)∵AC ⊥BC ,BD ⊥AD??????
∴?∠D= ∠C=90°???
在Rt△ACB和Rt △BDA中,AB= BA,AC=BD ,??
∴△ACB≌△BDA(HL)????
∴BC=AD;
(2)由△ACB≌?△BDA 得∠C AB=∠D BA?????????????
?∴△OAB是等腰三角形
板块二、等边三角形的性质与判定
如图,已知点B、C、D在同一条直线上,和都是等边三角形,BE交AC于F,
AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)求证:FH∥BD.
(1)证明:和都是等边三角形
∴BC=AC,CE=CD,∠BCA=∠ECD=60°
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD
在△BCE和△ACD中
false
∴△BCE≌△ACD(SAS)
(2)由(1)知△BCE≌△ACD
则∠CBF=∠CAH,BC=AC
又∵和都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF,
在△BCF和△ACH中
false
∴△BCF≌△ACH(ASA)
∴CF=CH,
又∵∠FCH=60°
∴△CHF是等边三角形
∴∠FHC=∠HCD=60°,
∴FH∥BD
例2、已知:如右图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接D,E,F,得到△DEF为等边
三角形.求证:(1)△AEF≌△CDE; (2)△ABC为等边三角形.
证明:(1)∵BF=AC,AB=AE,
∴FA=EC,
∵△DEF是等边三角形,
∴EF=DE,
又∵AE=CD(已知),
∴△AEF≌△CDE(SSS);
(2)由△AEF≌△CDE,得∠FEA=∠EDC,
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
△DEF是等边三角形,
∴∠DEF=60°,
∴∠BCA=60°,同理可得∠BAC=60°,
∴△ABC中,AB=BC,
∴△ABC是等边三角形。
板块三、线段的垂直平分线和角平分线
如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.则∠PAQ的度数为 30° .
-85725097155
例2、如右图,△ABC的周长为30 cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4 cm,则△ABD的周长是( A )
A.22 cm B.20 cm C.18 cm D.15 cm
708025114935
例3、如右图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
465455122555
解:∵在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,
∴∠DAE=?∠CAB=(90°-∠B),
∵DE垂直平分AB,
∴AD=BD,
∴∠DAE=∠B,
∴∠DAE=?∠CAB=?(90°-∠B)=∠B,
∴3∠B=90°,
∴∠B=30°.
例4.如图,AD为△ABC的角平分线,AD的中垂线交AB于点E、交BC的延长线于点F,AC于EF交于点O.
(1)求证:∠3=∠B; (2)连接OD,求证:∠B+∠ODB=180°.
证明:(1)∵AD为△ABC的角平分线,
∴∠1=∠2,
∵AD的中垂线交AB于点E、BC的延长线于点F,
∴AF=DF,
∴∠4=∠DAF=∠2+∠3,
∵∠4=∠1+∠B,
∴∠3=∠B;
(2)∵EF是AD的中垂线,
∴OA=OD,
∴∠2=∠ODA,
∵∠4=∠DAF,
∴∠3=∠ODF,
∵∠3=∠B,
∴∠ODF=∠B,
∴OD∥AB,
∴∠B+∠ODB=180°.
例5、如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交于点D,PE⊥OB交于点E,F是OC上除点P、O外一点,连接DF、EF,则DF与EF的关系如何?证明你的结论.
解:DF=EF.
理由如下:
∵OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交于点D,PE⊥OB交于点E,
∴PD=PE,
由HL定理易证△OPD≌△OPE,
∴∠OPD=∠OPE,∴∠DPF=∠EPF.
在△DPF与△EPF中,
,
∴△DPF≌△EPF,
∴DF=EF.
板块四、含30°的直角三角形
例1、如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.
求证:△OCD是等边三角形; (2)若EF=5,求线段OE的长.
解:(1)∵点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,
∴DE=CE,
在Rt△ODE和Rt△OCE中,
false
∴Rt△ODE≌Rt△OCE(LH)
∴OD=OC,
∵∠AOB=60°,
∴△OCD是等边三角形;
(2)∵△OCD是等边三角形,OF是角平分线,
∴OE⊥DC,
∵∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵∠ODF=60°,ED⊥OA,
∴∠EDF=30°,
∴DE=2EF=10,
∴OE=2DE=20.
例2、如图所示,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于点H,HD=1,HE=2,试求BD和CE的长.
解:∵BD⊥AC于D,∠A=60°,
∴∠ABD=90°-60°=30°,
在Rt△BEH中,∠HEB=90°,∠EBH=30°.
∴BH=2EH=4.
同理可得,CH=2HD=2,
∴BD=BH+HD=4+1=5.
CE=CH+HE=2+2=4.
