第14章勾股定理-华东师大版八年级数学上册复习讲义教案(Word版含答案)
文档属性
| 名称 | 第14章勾股定理-华东师大版八年级数学上册复习讲义教案(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 10:41:13 | ||
图片预览




文档简介
勾股定理
一、知识要点:
1、勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。也就是说:如果直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。公式的变形:a2 = c2- b2, b2= c2-a2 。
2、勾股定理的逆定理
如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点:
已知的条件:某三角形的三条边的长度.
②满足的条件:最大边的平方=最小边的平方+中间边的平方.
③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.
④如果不满足条件,就说明这个三角形不是直角三角形。
3、勾股数
满足a2 + b2= c2的三个正整数,称为勾股数。注意:①勾股数必须是正整数,不能是分数或小数。②一组勾股数扩大相同的正整数倍后,仍是勾股数。常见勾股数有:
(3,4,5?)(5,12,13?) (?6,8,10?)?(?7,24,25?)?
(?8,15,17?)(9,12,15?)?
最短距离问题:主要运用的依据是两点之间线段最短。
二、经典例题:
1、利用勾股定理求线段的长
例1、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)已知=2,=3,求;
(2)已知,=32,求、.
对应练习:如图,在false中,false,false于点false,false,false,求false,false的长.
2、利用勾股定理说明边的关系
例2、如图所示,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为N,
试说明.
3、利用勾股定理求面积
例3、如图,false中,false,以false、false为直径作半圆false和false,且false,则false的长为false false
A.16 B.8 C.4 D.2
对应练习:如图,其中所有三角形都是直角三角形,所有四边形都是正方形.若false,false,false,false和false分别代表相应的正方形的面积,且false,false,false,false,则false等于false false
A.25 B.31 C.32 D.40
4、利用勾股定理解直角三角形折叠问题
例4、长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
对应练习:如图,有一块直角三角形纸片,两直角边false,false,将纸片沿false折叠,直角边false恰好落在斜边上,且与false重合,求false的面积.
5、判断直角三角形
例5、在以线段false,false,false的长三边的三角形中,不能构成直角三角形的是false false
A.false,false,false B.false
C.false,false,false D.false,false,false
对应练习:)如图,在△ABC中,∠B=30°,∠C=45°,AC=2.求BC边上的高及△ABC的面积.
6、最短距离问题
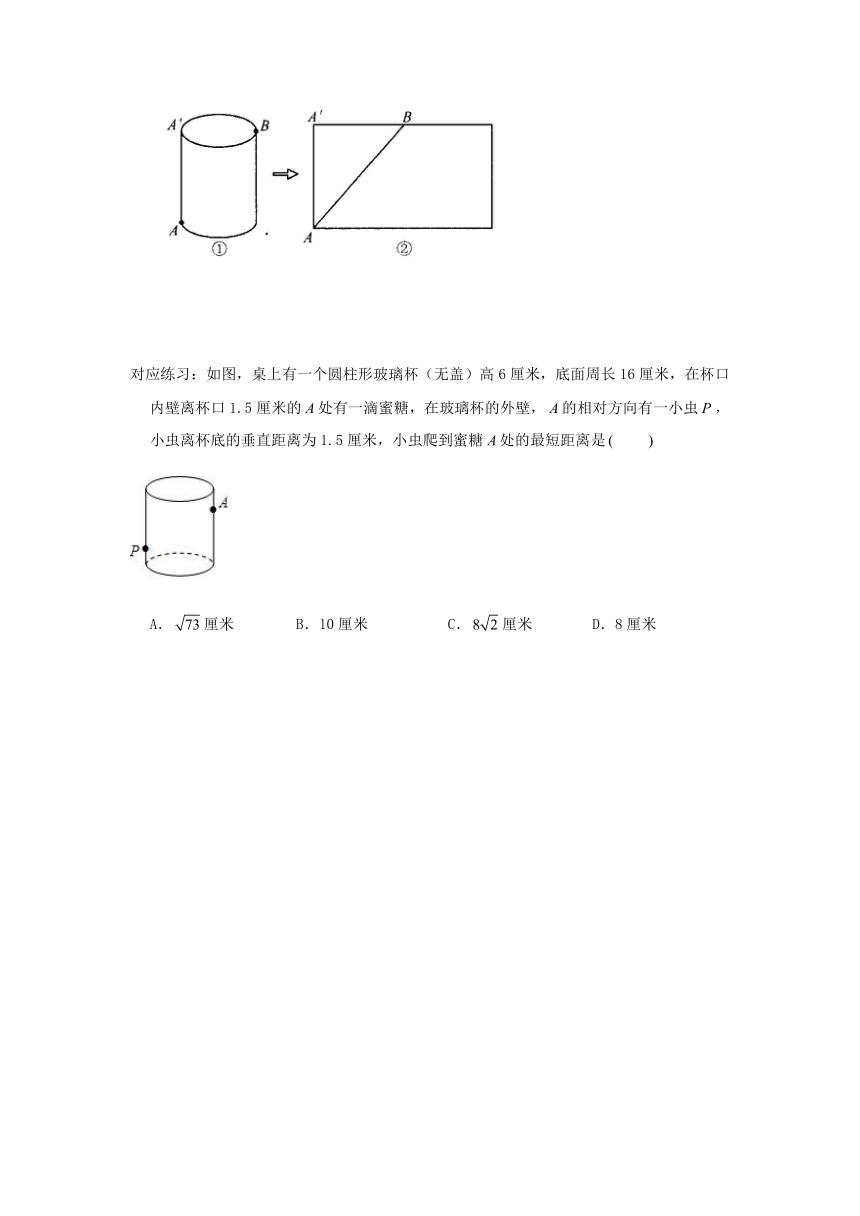
例6、如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)
对应练习:如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的false处有一滴蜜糖,在玻璃杯的外壁,false的相对方向有一小虫false,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖false处的最短距离是false false
A.false厘米 B.10厘米 C.false厘米 D.8厘米
勾股定理
一、知识要点:
1、勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。也就是说:如果直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。公式的变形:a2 = c2- b2, b2= c2-a2 。
2、勾股定理的逆定理
如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点:
已知的条件:某三角形的三条边的长度.
②满足的条件:最大边的平方=最小边的平方+中间边的平方.
③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.
④如果不满足条件,就说明这个三角形不是直角三角形。
3、勾股数
满足a2 + b2= c2的三个正整数,称为勾股数。注意:①勾股数必须是正整数,不能是分数或小数。②一组勾股数扩大相同的正整数倍后,仍是勾股数。常见勾股数有:
(3,4,5?)(5,12,13?) (?6,8,10?)?(?7,24,25?)?
(?8,15,17?)(9,12,15?)?
最短距离问题:主要运用的依据是两点之间线段最短。
二、经典例题:
1、利用勾股定理求线段的长
例1、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)已知=2,=3,求;
(2)已知,=32,求、.
解:(1)∵ ∠C=90°,=2,=3,
∴ ;
(2)设,.
∵ ∠C=90°,=32,
∴ .
即.
解得=8.
∴ ,.
对应练习:如图,在false中,false,false于点false,false,false,求false,false的长.
解:false,false,false,
false.
根据直角三角形的面积公式,得false.
在false中,false
2、利用勾股定理说明边的关系
例2、如图所示,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为N,
试说明.
解:∵MN⊥AB,所以,,
∴.
∵AM是中线,所以MC=MB.
又∵∠C=90°,∴在Rt△AMC中,,
∴.
3、利用勾股定理求面积
例3、如图,false中,false,以false、false为直径作半圆false和false,且false,则false的长为false false
A.16 B.8 C.4 D.2
解:由勾股定理得,false,
false,
解得,false,
则false,
解得,false,
故选:false.
对应练习:如图,其中所有三角形都是直角三角形,所有四边形都是正方形.若false,false,false,false和false分别代表相应的正方形的面积,且false,false,false,false,则false等于false false
A.25 B.31 C.32 D.40
解:如图,由题意得:
false,
false,
false,
false.故选:false.
4、利用勾股定理解直角三角形折叠问题
例4、长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,
△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.
∴x=(cm).
答:DE的长为cm.
对应练习:如图,有一块直角三角形纸片,两直角边false,false,将纸片沿false折叠,直角边false恰好落在斜边上,且与false重合,求false的面积.
解:false,false
false
false将纸片沿false折叠,直角边false恰好落在斜边上,且与false重合,
false,false
false
设false,
则在false中,false
解得false,
即false等于false
false的面积false
答:false的面积为false
5、判断直角三角形
例5、在以线段false,false,false的长三边的三角形中,不能构成直角三角形的是false false
A.false,false,false B.false
C.false,false,false D.false,false,false
解:false、false,不能构成直角三角形,故本选项符合题意;
false、设三角形三边为false,false,false,falsefalse,能构成直角三角形,故本选项不符合题意;
false、falsefalsefalsefalse,能构成直角三角形,故本选项不符合题意;
false、false,能构成直角三角形,故本选项不符合题意;
故选:false.
对应练习:)如图,在△ABC中,∠B=30°,∠C=45°,AC=2.求BC边上的高及△ABC的面积.
解:∵AD⊥BC,∠C=45°,
∴△ACD是等腰直角三角形,
∵AD=CD.
∵AC=2,
∴2AD2=AC2,即2AD2=8,解得AD=CD=2.
∵∠B=30°,
∴AB=2AD=4,
∴BD===2,
∴BC=BD+CD=2+2,
∴S△ABC=BC?AD=(2+2)×2=2+2.
6、最短距离问题
例6、如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)
解:如图②所示,由题意可得:
,
在Rt△AA′B中,根据勾股定理得:
则AB=15.
所以需要爬行的最短路程是15.
对应练习:如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的false处有一滴蜜糖,在玻璃杯的外壁,false的相对方向有一小虫false,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖false处的最短距离是false false
A.false厘米 B.10厘米 C.false厘米 D.8厘米
解:如图所示:最短路径为:false,将圆柱展开,
false,
最短路程为false.故选:false.
一、知识要点:
1、勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。也就是说:如果直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。公式的变形:a2 = c2- b2, b2= c2-a2 。
2、勾股定理的逆定理
如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点:
已知的条件:某三角形的三条边的长度.
②满足的条件:最大边的平方=最小边的平方+中间边的平方.
③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.
④如果不满足条件,就说明这个三角形不是直角三角形。
3、勾股数
满足a2 + b2= c2的三个正整数,称为勾股数。注意:①勾股数必须是正整数,不能是分数或小数。②一组勾股数扩大相同的正整数倍后,仍是勾股数。常见勾股数有:
(3,4,5?)(5,12,13?) (?6,8,10?)?(?7,24,25?)?
(?8,15,17?)(9,12,15?)?
最短距离问题:主要运用的依据是两点之间线段最短。
二、经典例题:
1、利用勾股定理求线段的长
例1、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)已知=2,=3,求;
(2)已知,=32,求、.
对应练习:如图,在false中,false,false于点false,false,false,求false,false的长.
2、利用勾股定理说明边的关系
例2、如图所示,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为N,
试说明.
3、利用勾股定理求面积
例3、如图,false中,false,以false、false为直径作半圆false和false,且false,则false的长为false false
A.16 B.8 C.4 D.2
对应练习:如图,其中所有三角形都是直角三角形,所有四边形都是正方形.若false,false,false,false和false分别代表相应的正方形的面积,且false,false,false,false,则false等于false false
A.25 B.31 C.32 D.40
4、利用勾股定理解直角三角形折叠问题
例4、长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
对应练习:如图,有一块直角三角形纸片,两直角边false,false,将纸片沿false折叠,直角边false恰好落在斜边上,且与false重合,求false的面积.
5、判断直角三角形
例5、在以线段false,false,false的长三边的三角形中,不能构成直角三角形的是false false
A.false,false,false B.false
C.false,false,false D.false,false,false
对应练习:)如图,在△ABC中,∠B=30°,∠C=45°,AC=2.求BC边上的高及△ABC的面积.
6、最短距离问题
例6、如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)
对应练习:如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的false处有一滴蜜糖,在玻璃杯的外壁,false的相对方向有一小虫false,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖false处的最短距离是false false
A.false厘米 B.10厘米 C.false厘米 D.8厘米
勾股定理
一、知识要点:
1、勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。也就是说:如果直角三角形的两直角边为a、b,斜边为c ,那么 a2 + b2= c2。公式的变形:a2 = c2- b2, b2= c2-a2 。
2、勾股定理的逆定理
如果三角形ABC的三边长分别是a,b,c,且满足a2 + b2= c2,那么三角形ABC 是直角三角形。这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点:
已知的条件:某三角形的三条边的长度.
②满足的条件:最大边的平方=最小边的平方+中间边的平方.
③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角.
④如果不满足条件,就说明这个三角形不是直角三角形。
3、勾股数
满足a2 + b2= c2的三个正整数,称为勾股数。注意:①勾股数必须是正整数,不能是分数或小数。②一组勾股数扩大相同的正整数倍后,仍是勾股数。常见勾股数有:
(3,4,5?)(5,12,13?) (?6,8,10?)?(?7,24,25?)?
(?8,15,17?)(9,12,15?)?
最短距离问题:主要运用的依据是两点之间线段最短。
二、经典例题:
1、利用勾股定理求线段的长
例1、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、.
(1)已知=2,=3,求;
(2)已知,=32,求、.
解:(1)∵ ∠C=90°,=2,=3,
∴ ;
(2)设,.
∵ ∠C=90°,=32,
∴ .
即.
解得=8.
∴ ,.
对应练习:如图,在false中,false,false于点false,false,false,求false,false的长.
解:false,false,false,
false.
根据直角三角形的面积公式,得false.
在false中,false
2、利用勾股定理说明边的关系
例2、如图所示,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为N,
试说明.
解:∵MN⊥AB,所以,,
∴.
∵AM是中线,所以MC=MB.
又∵∠C=90°,∴在Rt△AMC中,,
∴.
3、利用勾股定理求面积
例3、如图,false中,false,以false、false为直径作半圆false和false,且false,则false的长为false false
A.16 B.8 C.4 D.2
解:由勾股定理得,false,
false,
解得,false,
则false,
解得,false,
故选:false.
对应练习:如图,其中所有三角形都是直角三角形,所有四边形都是正方形.若false,false,false,false和false分别代表相应的正方形的面积,且false,false,false,false,则false等于false false
A.25 B.31 C.32 D.40
解:如图,由题意得:
false,
false,
false,
false.故选:false.
4、利用勾股定理解直角三角形折叠问题
例4、长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,
△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.
∴x=(cm).
答:DE的长为cm.
对应练习:如图,有一块直角三角形纸片,两直角边false,false,将纸片沿false折叠,直角边false恰好落在斜边上,且与false重合,求false的面积.
解:false,false
false
false将纸片沿false折叠,直角边false恰好落在斜边上,且与false重合,
false,false
false
设false,
则在false中,false
解得false,
即false等于false
false的面积false
答:false的面积为false
5、判断直角三角形
例5、在以线段false,false,false的长三边的三角形中,不能构成直角三角形的是false false
A.false,false,false B.false
C.false,false,false D.false,false,false
解:false、false,不能构成直角三角形,故本选项符合题意;
false、设三角形三边为false,false,false,falsefalse,能构成直角三角形,故本选项不符合题意;
false、falsefalsefalsefalse,能构成直角三角形,故本选项不符合题意;
false、false,能构成直角三角形,故本选项不符合题意;
故选:false.
对应练习:)如图,在△ABC中,∠B=30°,∠C=45°,AC=2.求BC边上的高及△ABC的面积.
解:∵AD⊥BC,∠C=45°,
∴△ACD是等腰直角三角形,
∵AD=CD.
∵AC=2,
∴2AD2=AC2,即2AD2=8,解得AD=CD=2.
∵∠B=30°,
∴AB=2AD=4,
∴BD===2,
∴BC=BD+CD=2+2,
∴S△ABC=BC?AD=(2+2)×2=2+2.
6、最短距离问题
例6、如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)
解:如图②所示,由题意可得:
,
在Rt△AA′B中,根据勾股定理得:
则AB=15.
所以需要爬行的最短路程是15.
对应练习:如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的false处有一滴蜜糖,在玻璃杯的外壁,false的相对方向有一小虫false,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖false处的最短距离是false false
A.false厘米 B.10厘米 C.false厘米 D.8厘米
解:如图所示:最短路径为:false,将圆柱展开,
false,
最短路程为false.故选:false.
