28.1锐角三角函数(第2课时) 课堂互动训练 (含答案)
文档属性
| 名称 | 28.1锐角三角函数(第2课时) 课堂互动训练 (含答案) | 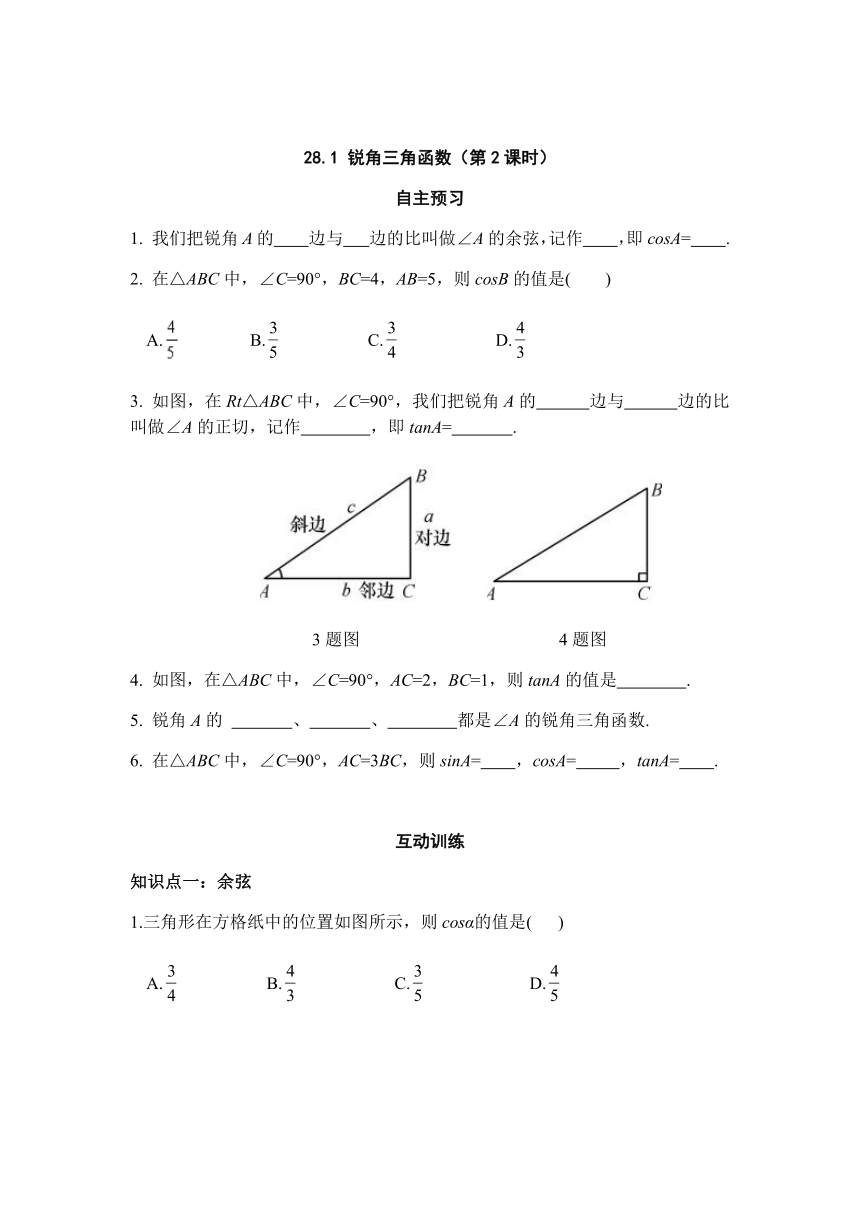 | |
| 格式 | docx | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 15:09:57 | ||
图片预览



文档简介
28.1 锐角三角函数(第2课时)
自主预习
1. 我们把锐角A的 边与 边的比叫做∠A的余弦,记作 ,即cosA= .
2. 在△ABC中,∠C=90°,BC=4,AB=5,则cosB的值是( )
A. B. C. D.
3. 如图,在Rt△ABC中,∠C=90°,我们把锐角A的 边与 边的比叫做∠A的正切,记作 ,即tanA= .
3题图 4题图
4. 如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
5. 锐角A的 、 、 都是∠A的锐角三角函数.
6. 在△ABC中,∠C=90°,AC=3BC,则sinA= ,cosA= ,tanA= .
互动训练
知识点一:余弦
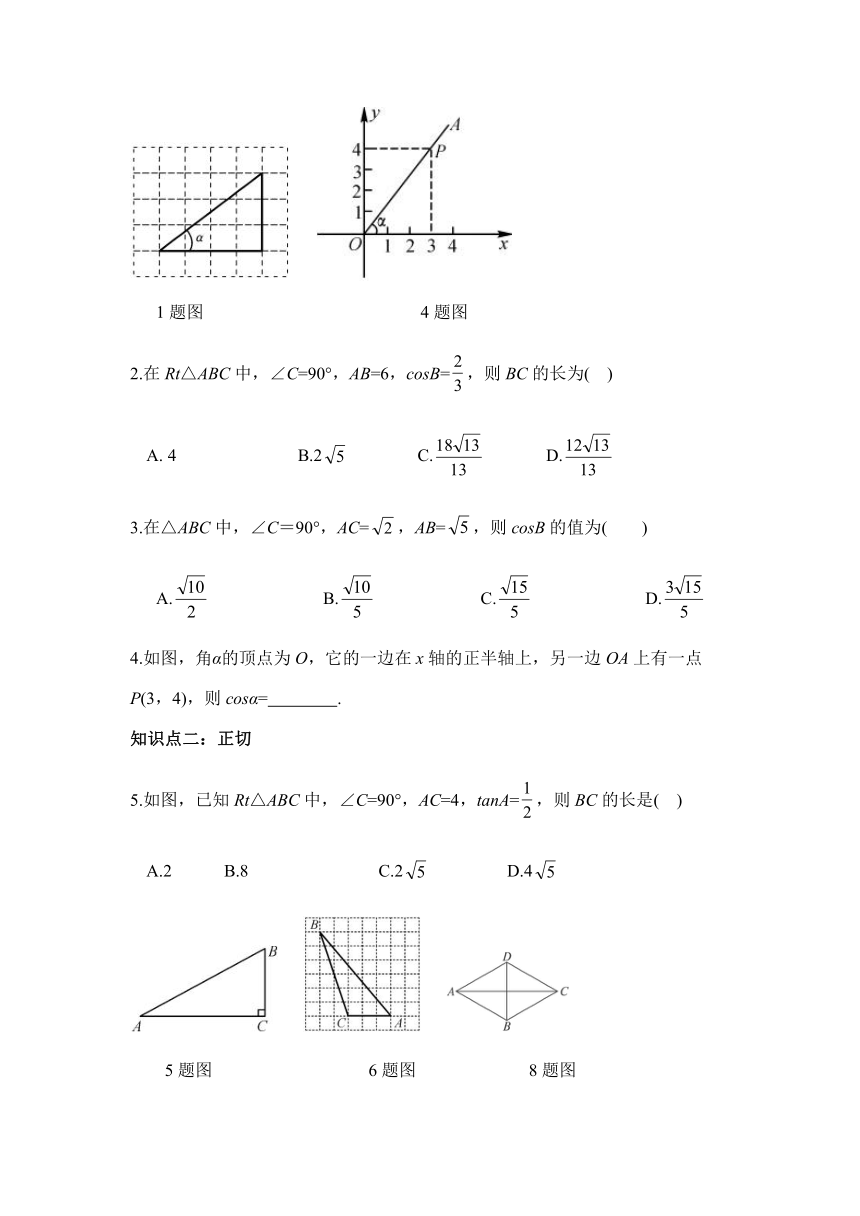
1.三角形在方格纸中的位置如图所示,则cosα的值是( )
A. B. C. D.
1题图 4题图
2.在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A. 4 B.2 C. D.
3.在△ABC中,∠C=90°,AC=false,AB=false,则cosB的值为( )
A.false B.false C.false D.false
4.如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点
P(3,4),则cosα= .
知识点二:正切
5.如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( )
A.2 B.8 C.2 D.4
5题图 6题图 8题图
6.如图,△ABC的三个顶点分别在正方形网格的格点上,则tanA的值是( )
A. B. C. D.
7.在△ABC中,∠C=90°,AB=3AC,则tanA=( )
A. B.3 C.2 D.
8.如图, 已知菱形ABCD,对角线AC=10 cm,BD=6 cm,那么tanfalse等于( )
A.false B.false C.false D.false
9.已知等腰三角形的腰长为6 cm,底边长为10 cm,则底角的正切值为 .
知识点三:锐角三角函数
10.在Rt△ACB中,∠C=90°,AB=10,sinA=,cosA=,tanA=,则BC的长为( )
A.6 B.7.5 C.8 D.12.5
11.在Rt△ABC中,∠C=90°,已知tanB=false,则cosA等于( )
A.false B.false C.false D.false
12. 如果∠A为锐角,那么sin∠A ( )
A.小于1 B.等于1 C.大于1 D.大于零且小于1
13.在Rt△ABC中,∠C=90°,AC=7,BC=24.
(1)求AB的长;
(2)求sinA,cosA,tanA的值.
课时达标
1.在Rt△ABC中,∠C=90°,BC=4,sinA=false,则AB的长为( )
A.false B.6 C.12 D.8
2.在Rt△ABC中,∠C=90°,cosA=,AC=6 cm,那么BC等于( )
A.8 cm B. cm C. cm D.cm
3.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α, tanα=,则t的值是( )
A.1 B.1.5 C.2 D.3
3题图 6题图 7题图
4.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB=( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值是( )
A. B. C. D.
6.如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A. B. C. D.
7.如图,∠1的正切值等于 .
8.如图所示,在Rt△ABC中,∠C=90°,sinA=,求cosA,tanB的值.
8题图
9.如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
9题图
10. 在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,且a=3,c=5,求∠A、∠B的三角函数值.
11.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,且b=6,
tanA=1,求c.
12.如图,在Rt△ABC中,∠C=90°,sinA=false,D为AC上一点,∠BDC=45°,DC=6 cm,求AB、AD的长.
12题图
拓展探究
1.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果,求tan∠DCF的值.
2.如图所示,在△ABC中,D是AB的中点,DC⊥AC,且tan∠BCD=false,
求sinA,cosA,tanA的值.
2题图
28.1 锐角三角函数(第2课时)答案
自主预习
1. 邻 斜 cosA false, 2. A. 3. 对 邻 tanA false, 4. false
5. 正弦 余弦 正切 6. false false false
互动训练
1. D. 2. A.
3. C. 解析:由勾股定理, 得BC=false,∴cosB=false.答案:C.
4. false 5. A. 6. A. 7. C.
8. A. 解析:菱形的对角线互相垂直且平分,由三角函数定义,
得tanfalse=tan∠DAC=false. 答案:A.
9.false 10. A.
11. B. 解析:tanB=false,设b=falsek,a=2k. ∴c=3k.
∴cosA=false. 答案:B.
12. D.
13.(1)由勾股定理得AB=false=false=25.
(2)sinA=false=false,cosA=false=false,tanA=false=false.
课时达标
1. B. 解析:sinA=false=false,AB=6.
2. A. 3. C. 4. C. 5. B. 6. B. 7.false
8.∵sinA=false, ∴设BC=falsek,AB=3k(k>0).
由勾股定理得AC=false=false=falsek.
∴cosA=false,tanA=false.
9.在Rt△ACD中,CD=6,tanA=false, ∴false=false=false,即AD=4.
又AB=12, ∴BD=AB-AD=8.
在Rt△BCD中,BC=false=10.
∴sinB=false=false=false,cosB=false=false=false. ∴sinB+cosB=false+false=false.
10.解:根据勾股定理得b=4,
∴ sinA=false,cosA=false,tanA=false;sinB=false,cosB=false,tanB=false.
11. 解:由三角函数定义知a=btanA,所以a=6,根据勾股定理得c=false.
12. 解:如题图,在Rt△BCD中,∠BDC=45°,
∴BC=DC=6.在Rt△ABC中,sinA=false,∴false=false.∴AB=10.
∴AC=false=8. ∴AD=AC-CD=8-6=2.
拓展探究
1.∵四边形ABCD是矩形, ∴AB=CD,∠D=90°.
∵false=false, 且由折叠知CF=BC, ∴false=false.
设CD=2x,CF=3x(x>0), ∴DF=false=falsex.
∴tan∠DCF=false=false=false.
2.过点D作CD⊥DE交BC于点E.
在Rt△CDE中,∵tan∠BCD=false,
设DE=x,则CD=3x.
又∵DC⊥AC,∴DE∥AC,∴△DEB∽△ACB,
∴false, ∵AD=BD=falseAB,∴BE=CE=falseBC.
∴DE=falseAC,∴AC=2DE=2x.
在Rt△ACD中,AC=2x,CD=3x.
∴AD=falsex.
∴sinA=false,tanA=false.
自主预习
1. 我们把锐角A的 边与 边的比叫做∠A的余弦,记作 ,即cosA= .
2. 在△ABC中,∠C=90°,BC=4,AB=5,则cosB的值是( )
A. B. C. D.
3. 如图,在Rt△ABC中,∠C=90°,我们把锐角A的 边与 边的比叫做∠A的正切,记作 ,即tanA= .
3题图 4题图
4. 如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
5. 锐角A的 、 、 都是∠A的锐角三角函数.
6. 在△ABC中,∠C=90°,AC=3BC,则sinA= ,cosA= ,tanA= .
互动训练
知识点一:余弦
1.三角形在方格纸中的位置如图所示,则cosα的值是( )
A. B. C. D.
1题图 4题图
2.在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A. 4 B.2 C. D.
3.在△ABC中,∠C=90°,AC=false,AB=false,则cosB的值为( )
A.false B.false C.false D.false
4.如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点
P(3,4),则cosα= .
知识点二:正切
5.如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( )
A.2 B.8 C.2 D.4
5题图 6题图 8题图
6.如图,△ABC的三个顶点分别在正方形网格的格点上,则tanA的值是( )
A. B. C. D.
7.在△ABC中,∠C=90°,AB=3AC,则tanA=( )
A. B.3 C.2 D.
8.如图, 已知菱形ABCD,对角线AC=10 cm,BD=6 cm,那么tanfalse等于( )
A.false B.false C.false D.false
9.已知等腰三角形的腰长为6 cm,底边长为10 cm,则底角的正切值为 .
知识点三:锐角三角函数
10.在Rt△ACB中,∠C=90°,AB=10,sinA=,cosA=,tanA=,则BC的长为( )
A.6 B.7.5 C.8 D.12.5
11.在Rt△ABC中,∠C=90°,已知tanB=false,则cosA等于( )
A.false B.false C.false D.false
12. 如果∠A为锐角,那么sin∠A ( )
A.小于1 B.等于1 C.大于1 D.大于零且小于1
13.在Rt△ABC中,∠C=90°,AC=7,BC=24.
(1)求AB的长;
(2)求sinA,cosA,tanA的值.
课时达标
1.在Rt△ABC中,∠C=90°,BC=4,sinA=false,则AB的长为( )
A.false B.6 C.12 D.8
2.在Rt△ABC中,∠C=90°,cosA=,AC=6 cm,那么BC等于( )
A.8 cm B. cm C. cm D.cm
3.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α, tanα=,则t的值是( )
A.1 B.1.5 C.2 D.3
3题图 6题图 7题图
4.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB=( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值是( )
A. B. C. D.
6.如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A. B. C. D.
7.如图,∠1的正切值等于 .
8.如图所示,在Rt△ABC中,∠C=90°,sinA=,求cosA,tanB的值.
8题图
9.如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
9题图
10. 在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,且a=3,c=5,求∠A、∠B的三角函数值.
11.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,且b=6,
tanA=1,求c.
12.如图,在Rt△ABC中,∠C=90°,sinA=false,D为AC上一点,∠BDC=45°,DC=6 cm,求AB、AD的长.
12题图
拓展探究
1.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果,求tan∠DCF的值.
2.如图所示,在△ABC中,D是AB的中点,DC⊥AC,且tan∠BCD=false,
求sinA,cosA,tanA的值.
2题图
28.1 锐角三角函数(第2课时)答案
自主预习
1. 邻 斜 cosA false, 2. A. 3. 对 邻 tanA false, 4. false
5. 正弦 余弦 正切 6. false false false
互动训练
1. D. 2. A.
3. C. 解析:由勾股定理, 得BC=false,∴cosB=false.答案:C.
4. false 5. A. 6. A. 7. C.
8. A. 解析:菱形的对角线互相垂直且平分,由三角函数定义,
得tanfalse=tan∠DAC=false. 答案:A.
9.false 10. A.
11. B. 解析:tanB=false,设b=falsek,a=2k. ∴c=3k.
∴cosA=false. 答案:B.
12. D.
13.(1)由勾股定理得AB=false=false=25.
(2)sinA=false=false,cosA=false=false,tanA=false=false.
课时达标
1. B. 解析:sinA=false=false,AB=6.
2. A. 3. C. 4. C. 5. B. 6. B. 7.false
8.∵sinA=false, ∴设BC=falsek,AB=3k(k>0).
由勾股定理得AC=false=false=falsek.
∴cosA=false,tanA=false.
9.在Rt△ACD中,CD=6,tanA=false, ∴false=false=false,即AD=4.
又AB=12, ∴BD=AB-AD=8.
在Rt△BCD中,BC=false=10.
∴sinB=false=false=false,cosB=false=false=false. ∴sinB+cosB=false+false=false.
10.解:根据勾股定理得b=4,
∴ sinA=false,cosA=false,tanA=false;sinB=false,cosB=false,tanB=false.
11. 解:由三角函数定义知a=btanA,所以a=6,根据勾股定理得c=false.
12. 解:如题图,在Rt△BCD中,∠BDC=45°,
∴BC=DC=6.在Rt△ABC中,sinA=false,∴false=false.∴AB=10.
∴AC=false=8. ∴AD=AC-CD=8-6=2.
拓展探究
1.∵四边形ABCD是矩形, ∴AB=CD,∠D=90°.
∵false=false, 且由折叠知CF=BC, ∴false=false.
设CD=2x,CF=3x(x>0), ∴DF=false=falsex.
∴tan∠DCF=false=false=false.
2.过点D作CD⊥DE交BC于点E.
在Rt△CDE中,∵tan∠BCD=false,
设DE=x,则CD=3x.
又∵DC⊥AC,∴DE∥AC,∴△DEB∽△ACB,
∴false, ∵AD=BD=falseAB,∴BE=CE=falseBC.
∴DE=falseAC,∴AC=2DE=2x.
在Rt△ACD中,AC=2x,CD=3x.
∴AD=falsex.
∴sinA=false,tanA=false.
