28.2.1解直角三角形 课堂互动训练(含答案)
文档属性
| 名称 | 28.2.1解直角三角形 课堂互动训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 419.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 15:13:23 | ||
图片预览




文档简介
28.2.1 解直角三角形
自主预习
1.解直角三角形的依据(∠C=90°):
(1)三边之间的关系: (勾股定理);
(2)两锐角之间的关系: ;
(3)边角之间关系:sinA= ,sinB= ;cosA= ,cosB= ;
tanA= ,tanB= .
2. 如图,已知∠C=90°,∠A=28°,AC=6米,AB≈ 米.(精确到0.1)
互动训练
知识点一: 已知两边解直角三角形
1.在△ABC中,∠C=90°,AC=3,AB=4,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出 B.计算sinA的值求出
C.计算cosA的值求出 D.先根据sinB求出∠B,再利用90°-∠B求出
2.在Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )
A. B.false C.false D.false
3.在Rt△ABC中,AB=4,AC=2false,∠C=90°,则∠A的度数为( )
A.30° B.40° C.45° D.60°
4.在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,∠C=90°,a=5,
c=5false,则∠B= ,b= .
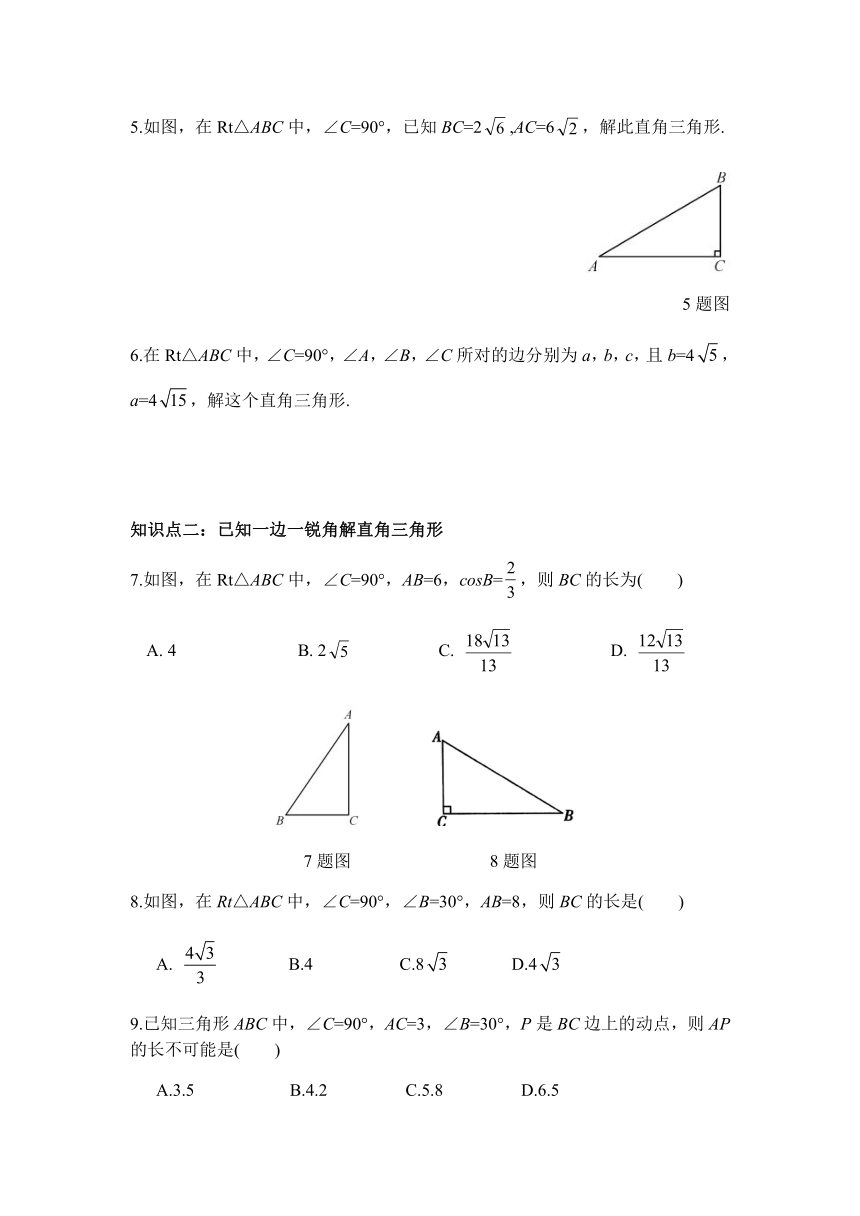
5.如图,在Rt△ABC中,∠C=90°,已知BC=2false,AC=6false,解此直角三角形.
5题图
6.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=4false,a=4false,解这个直角三角形.
知识点二:已知一边一锐角解直角三角形
7.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=false,则BC的长为( )
A. 4 B. 2false C. false D. false
7题图 8题图
8.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. false B.4 C.8false D.4false
9.已知三角形ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP的长不可能是( )
A.3.5 B.4.2 C.5.8 D.6.5
10.如果等腰三角形的底角为30°,腰长为6 cm,那么这个三角形的面积为( )
A.4.5 cm2 B.9false cm2 C.18false cm2 D.36 cm2
11.在Rt△ABC中,CA=CB,AB=9false,点D在BC边上,连接AD,若tan∠CAD=false,则BD的长为 .
12.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.求下列直角三角形中的未知量.
(1)∠B=60°,c=25; (2)∠A=30°,b=false.
13.在Rt△ABC中,∠C=90°,c=8false,∠A=60°,解这个直角三角形.
14.如图,在Rt△ABC中,∠C=90°,∠B=55°,AC=4,解此直角三角形.(结果保留小数点后一位)
14题图
知识点三:解直角三角形的综合应用
15.在△ABC中,∠A,∠B均为锐角,且sinA=false,cosB=false,AC=40,则△ABC的面积是( )
A.800 B.800false C.400 D.400false
16.如图,已知在△ABC中,AD是边BC上的高,BC=14,AD=12,sinB=false,则线段DC的长为( )
A.3 B.4 C.5 D.6
16题图 17题图
17.如图,平面直角坐标系中有正方形ABCD,B(0,false),∠BA0=60°,那么点C的坐标为 ____.
18.在△ABC中,AC=6,BC=5,sinA=false,∠A,∠B为锐角,求tanB的值.
19.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E. (注意:本题中的计算过程和结果均保留根号)
(1)若∠A=60°,求BC的长;
(2)若sinA=false,求AD的长.
19题图
课时达标
1.在Rt△ABC中,∠C=90°,已知∠A,b,解此直角三角形就是要求出( )
A.c B.a,c
C.∠B,a,c D.∠B,a,c,△ABC的面积
2.在Rt△ABC中,若∠C=90°,AC=1,BC=2,则下列结论中正确的是( )
A.sinB=false B.cosB=false C.tanB=2 D.cosB=false
3.如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,false,则下列结论正确的个数是( )
①DE=3 cm;②BE=1 cm;③菱形的面积为15 cm2;④BD=falsecm.
A.1个 B.2个 C.3个 D.4个
3题图 4题图
4.如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC= .
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
5.根据下列条件解Rt△ABC(∠C=90°).
(1)∠A=30°,b=false; (2)c=4,b=2false.
6.如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10false,AB=20.求∠A的度数.
6题图
7.如图,在△ABC中,∠A=30°,∠B=45°,AC=2false,求AB的长.
7题图
8.如图,C、D是半圆O上两点,false,求cos∠CEB和tan∠CEB.
8题图
9.如图所示,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的关系,并说明理由.
(2)若⊙O的半径为3 cm,,AE=5 cm.求∠ADE的正弦值.
9题图
拓展探究
1.探究:已知如图1,在△ABC中,∠A=α(0°<α<90°),AB=c,AC=b,试用含b,c,α的式子表示△ABC的面积;
应用:如图2,在平行四边形ABCD中,对角线AC、BD相交成的锐角为α,若AC=a,BD=b,试用含b,c,α的式子表示平行四边形ABCD的面积.
28.2.1 解直角三角形答案
自主预习
1. (1) a2+b2=c2 (2) ∠A+∠B=90° (3)false false false false false false
2. 6.8
互动训练
1. C. 2. A.
3.C.解析:在Rt△ABC中,∵AB=4,AC=2false,∠C=90°,
∴cosA=false=false=,∴∠A=45°.故选C.
4.45°,5. 解析:∵sinA=false=false=false,∴∠A=45°,∴∠B=90°-∠A=45°,∴∠B=∠A,∴b=a=5.
5.解:∵tanA=false=false=false, ∴∠A=30°.
∴∠B=90°-∠A=90°-30°=60°,AB=2BC=4false.
6.解:在Rt△ABC中,∵∠C=90°,b=4false,a=4false,∴tanA=false=false=false,∴∠A=60°,∴∠B=90°-∠A=30°,∴c=2b=8false.
故c=8false,∠A=60°,∠B=30°.
7. A.
8. D. 解析:在Rt△ABC中,∵∠C=90°,∠B=30°,AB=8,
∴BC=ABcosB=8×false=4false.故选D.
9.D. 解析:根据垂线段最短,可知AP的长不可能小于3.在△ABC中,∠C=90°,AC=3,∠B=30°,∴AB=6,∴AP的长不可能大于6.故选D.
10. B. 11. 6.
12.解:(1)在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°,∴sinA=false=false, ∵c=25,∴a=false.
∵cosA=false=false,c=25,∴b=false.
综上a=false, b=false,∠A=30°.
(2) ∵∠C=90°,∠A=30°,∴∠B=60°.
在Rt△ABC中,cosA=false=false,∵b=false,∴c=2,∴a=falsec=1.
综上,a=l,c=2,∠B=60°.
13.解:∵∠A=60°, ∴∠B=90°-∠A=30°.
∵sinA=false, ∴a=c·sinA=8false×sin60°=8false×false=12,
∴b=false=false=4false.
14.解:∠A=90°-∠B=90°-55°=35°.
∵tanB=false,∴BC=false=false≈2.8.
∵sinB=false,∴AB=false=false≈4.9.
15. D. 解析:∴sinA=false,cosB=false,∴∠A=∠B=30°,∴BC=AC.
如图,过点C作CD⊥AB于点D,则CD=falseAC=20,AD=20false,
∴AB=2AD=40false,∴S△ABC=falseAB·CD=400false. 故选D.
15题图
16. C. 解析:∵AD是边BC上的高,∴AD⊥BC.
在Rt△BDA中,∠BDA=90°,AD=12,sinB=false=false,
∴AB=15,∴BD=false=false=9,
DC=BC-BD=14-9=5. 故选C.
17. (-false, false+1). 解析:过点C作CE⊥y轴于点E,
则Rt△CEB≌Rt△BOA,∴CE=BO=false,BE=AO=false=l,
∴OE=OB+BE=false+1,∴点C的坐标为(-false,false+1) .
18.解:如图,过点C作CD⊥AB于点D,则sinA=false=false,∴CD=falseAC=4.
在Rt△BCD,BC=5,CD=4,∴BD=3,∴tanB=false=false.
19.解:(1)∵∠A=60o,∠ABE=90°,∴∠E=30°.
在Rt△ABE中,∵AB=6,tanA=false,∴BE=AB·tanA=6×tan60°=6false.
∵∠CDE=90°,CD=4,sinE=false,
∴CE=false=false=8,BC=BE-CE=6false-8.
(2)∵∠ABE=90°,AB=6,sinA=false=false,∴设BE=4x,AE=5x,则AB=3x,∴3x=6,得x=2,∴BE=8,AE=10,∴tanE=false=false=false=false,解得DE=false,
∴AD=AE-DE=10-false=false.
19题图
课时达标
1. C. 2. A.
3. C. 解析:由菱形的周长为20 cm知菱形边长是5 cm.
在Rt△ADE中,∵ AD=5 cm,sin A=false,∴ DE=AD·sinA=false(cm).
∴ false(cm).∴ BE=AB-AE=5-4=1(cm).
菱形的面积为AB·DE=5×3=15(cm2).
在Rt△DEB中,false(cm).
综上所述①②③正确.故选C.
4. 24.
5.(1)∠B=90°-∠A=90°-30°=60°. ∵tanA=false,∴a=b·tanA=false×false=1. ∴c=2a=2.
(2)由勾股定理得:a=false=false=2false.
∵b=2false,a=2false,∠C=90°, ∴∠A=∠B=45°.
6.在Rt△BDC中,∵sin∠BDC=false,
∴BC=BD×sin∠BDC=10false×sin45°=10.
在Rt△ABC中,∵sin∠A=false=false=false,∴∠A=30°.
7.过C作CD⊥AB于D,则∠ADC=∠BDC=90°.
∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD.
∵∠A=30°,AC=2false,∴CD=false,∴BD=CD=false.
由勾股定理得:AD=false=3. ∴AB=AD+BD=3+false.
8. 解:如图,连结BC,则∠ACB=90°,△ECD∽△EBA,
∴false,cos∠CEB=false tan∠CEB=false
8题图
9. 解: (1)CD与⊙O相切.
理由:如图所示,连接OD,则∠AOD=2∠AED=2×45°=90°.
∵ 四边形ABCD是平行四边形,∴ AB∥DC,
∴ ∠CDO=∠AOD=90°,∴ OD⊥CD,∴CD与⊙O相切.
(2)如图所示,连接BE,则∠ADE=∠ABE.
∵AB是⊙O的直径,∴∠AEB=90°,AB=2×3=6(cm).
在Rt△ABE中,false.
∴sin∠ADE=sin∠ABEfalse.
9题图
拓展探究
1.探究:过点B作BD⊥AC,垂足为D.
∵AB=c,∠A=α,∴BD=c·sinα. ∴S△ABC=falseAC·BD=falsebcsinα.
应用:过点C作CE⊥DO于点E. ∴sinα=false.
∵在□ABCD中,AC=a,BD=b,∴CO=falsea,DO=falseb.
∴S△COD=falseCO·DO·sinα=18absinα.
∴S△BCD=falseCE×BD=false×falseasinα×b=falseabsinα,
∴S□ABCD=2S△BCD=falseabsinα.
自主预习
1.解直角三角形的依据(∠C=90°):
(1)三边之间的关系: (勾股定理);
(2)两锐角之间的关系: ;
(3)边角之间关系:sinA= ,sinB= ;cosA= ,cosB= ;
tanA= ,tanB= .
2. 如图,已知∠C=90°,∠A=28°,AC=6米,AB≈ 米.(精确到0.1)
互动训练
知识点一: 已知两边解直角三角形
1.在△ABC中,∠C=90°,AC=3,AB=4,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出 B.计算sinA的值求出
C.计算cosA的值求出 D.先根据sinB求出∠B,再利用90°-∠B求出
2.在Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )
A. B.false C.false D.false
3.在Rt△ABC中,AB=4,AC=2false,∠C=90°,则∠A的度数为( )
A.30° B.40° C.45° D.60°
4.在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,∠C=90°,a=5,
c=5false,则∠B= ,b= .
5.如图,在Rt△ABC中,∠C=90°,已知BC=2false,AC=6false,解此直角三角形.
5题图
6.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=4false,a=4false,解这个直角三角形.
知识点二:已知一边一锐角解直角三角形
7.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=false,则BC的长为( )
A. 4 B. 2false C. false D. false
7题图 8题图
8.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. false B.4 C.8false D.4false
9.已知三角形ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP的长不可能是( )
A.3.5 B.4.2 C.5.8 D.6.5
10.如果等腰三角形的底角为30°,腰长为6 cm,那么这个三角形的面积为( )
A.4.5 cm2 B.9false cm2 C.18false cm2 D.36 cm2
11.在Rt△ABC中,CA=CB,AB=9false,点D在BC边上,连接AD,若tan∠CAD=false,则BD的长为 .
12.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.求下列直角三角形中的未知量.
(1)∠B=60°,c=25; (2)∠A=30°,b=false.
13.在Rt△ABC中,∠C=90°,c=8false,∠A=60°,解这个直角三角形.
14.如图,在Rt△ABC中,∠C=90°,∠B=55°,AC=4,解此直角三角形.(结果保留小数点后一位)
14题图
知识点三:解直角三角形的综合应用
15.在△ABC中,∠A,∠B均为锐角,且sinA=false,cosB=false,AC=40,则△ABC的面积是( )
A.800 B.800false C.400 D.400false
16.如图,已知在△ABC中,AD是边BC上的高,BC=14,AD=12,sinB=false,则线段DC的长为( )
A.3 B.4 C.5 D.6
16题图 17题图
17.如图,平面直角坐标系中有正方形ABCD,B(0,false),∠BA0=60°,那么点C的坐标为 ____.
18.在△ABC中,AC=6,BC=5,sinA=false,∠A,∠B为锐角,求tanB的值.
19.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E. (注意:本题中的计算过程和结果均保留根号)
(1)若∠A=60°,求BC的长;
(2)若sinA=false,求AD的长.
19题图
课时达标
1.在Rt△ABC中,∠C=90°,已知∠A,b,解此直角三角形就是要求出( )
A.c B.a,c
C.∠B,a,c D.∠B,a,c,△ABC的面积
2.在Rt△ABC中,若∠C=90°,AC=1,BC=2,则下列结论中正确的是( )
A.sinB=false B.cosB=false C.tanB=2 D.cosB=false
3.如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,false,则下列结论正确的个数是( )
①DE=3 cm;②BE=1 cm;③菱形的面积为15 cm2;④BD=falsecm.
A.1个 B.2个 C.3个 D.4个
3题图 4题图
4.如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC= .
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
5.根据下列条件解Rt△ABC(∠C=90°).
(1)∠A=30°,b=false; (2)c=4,b=2false.
6.如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10false,AB=20.求∠A的度数.
6题图
7.如图,在△ABC中,∠A=30°,∠B=45°,AC=2false,求AB的长.
7题图
8.如图,C、D是半圆O上两点,false,求cos∠CEB和tan∠CEB.
8题图
9.如图所示,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的关系,并说明理由.
(2)若⊙O的半径为3 cm,,AE=5 cm.求∠ADE的正弦值.
9题图
拓展探究
1.探究:已知如图1,在△ABC中,∠A=α(0°<α<90°),AB=c,AC=b,试用含b,c,α的式子表示△ABC的面积;
应用:如图2,在平行四边形ABCD中,对角线AC、BD相交成的锐角为α,若AC=a,BD=b,试用含b,c,α的式子表示平行四边形ABCD的面积.
28.2.1 解直角三角形答案
自主预习
1. (1) a2+b2=c2 (2) ∠A+∠B=90° (3)false false false false false false
2. 6.8
互动训练
1. C. 2. A.
3.C.解析:在Rt△ABC中,∵AB=4,AC=2false,∠C=90°,
∴cosA=false=false=,∴∠A=45°.故选C.
4.45°,5. 解析:∵sinA=false=false=false,∴∠A=45°,∴∠B=90°-∠A=45°,∴∠B=∠A,∴b=a=5.
5.解:∵tanA=false=false=false, ∴∠A=30°.
∴∠B=90°-∠A=90°-30°=60°,AB=2BC=4false.
6.解:在Rt△ABC中,∵∠C=90°,b=4false,a=4false,∴tanA=false=false=false,∴∠A=60°,∴∠B=90°-∠A=30°,∴c=2b=8false.
故c=8false,∠A=60°,∠B=30°.
7. A.
8. D. 解析:在Rt△ABC中,∵∠C=90°,∠B=30°,AB=8,
∴BC=ABcosB=8×false=4false.故选D.
9.D. 解析:根据垂线段最短,可知AP的长不可能小于3.在△ABC中,∠C=90°,AC=3,∠B=30°,∴AB=6,∴AP的长不可能大于6.故选D.
10. B. 11. 6.
12.解:(1)在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°,∴sinA=false=false, ∵c=25,∴a=false.
∵cosA=false=false,c=25,∴b=false.
综上a=false, b=false,∠A=30°.
(2) ∵∠C=90°,∠A=30°,∴∠B=60°.
在Rt△ABC中,cosA=false=false,∵b=false,∴c=2,∴a=falsec=1.
综上,a=l,c=2,∠B=60°.
13.解:∵∠A=60°, ∴∠B=90°-∠A=30°.
∵sinA=false, ∴a=c·sinA=8false×sin60°=8false×false=12,
∴b=false=false=4false.
14.解:∠A=90°-∠B=90°-55°=35°.
∵tanB=false,∴BC=false=false≈2.8.
∵sinB=false,∴AB=false=false≈4.9.
15. D. 解析:∴sinA=false,cosB=false,∴∠A=∠B=30°,∴BC=AC.
如图,过点C作CD⊥AB于点D,则CD=falseAC=20,AD=20false,
∴AB=2AD=40false,∴S△ABC=falseAB·CD=400false. 故选D.
15题图
16. C. 解析:∵AD是边BC上的高,∴AD⊥BC.
在Rt△BDA中,∠BDA=90°,AD=12,sinB=false=false,
∴AB=15,∴BD=false=false=9,
DC=BC-BD=14-9=5. 故选C.
17. (-false, false+1). 解析:过点C作CE⊥y轴于点E,
则Rt△CEB≌Rt△BOA,∴CE=BO=false,BE=AO=false=l,
∴OE=OB+BE=false+1,∴点C的坐标为(-false,false+1) .
18.解:如图,过点C作CD⊥AB于点D,则sinA=false=false,∴CD=falseAC=4.
在Rt△BCD,BC=5,CD=4,∴BD=3,∴tanB=false=false.
19.解:(1)∵∠A=60o,∠ABE=90°,∴∠E=30°.
在Rt△ABE中,∵AB=6,tanA=false,∴BE=AB·tanA=6×tan60°=6false.
∵∠CDE=90°,CD=4,sinE=false,
∴CE=false=false=8,BC=BE-CE=6false-8.
(2)∵∠ABE=90°,AB=6,sinA=false=false,∴设BE=4x,AE=5x,则AB=3x,∴3x=6,得x=2,∴BE=8,AE=10,∴tanE=false=false=false=false,解得DE=false,
∴AD=AE-DE=10-false=false.
19题图
课时达标
1. C. 2. A.
3. C. 解析:由菱形的周长为20 cm知菱形边长是5 cm.
在Rt△ADE中,∵ AD=5 cm,sin A=false,∴ DE=AD·sinA=false(cm).
∴ false(cm).∴ BE=AB-AE=5-4=1(cm).
菱形的面积为AB·DE=5×3=15(cm2).
在Rt△DEB中,false(cm).
综上所述①②③正确.故选C.
4. 24.
5.(1)∠B=90°-∠A=90°-30°=60°. ∵tanA=false,∴a=b·tanA=false×false=1. ∴c=2a=2.
(2)由勾股定理得:a=false=false=2false.
∵b=2false,a=2false,∠C=90°, ∴∠A=∠B=45°.
6.在Rt△BDC中,∵sin∠BDC=false,
∴BC=BD×sin∠BDC=10false×sin45°=10.
在Rt△ABC中,∵sin∠A=false=false=false,∴∠A=30°.
7.过C作CD⊥AB于D,则∠ADC=∠BDC=90°.
∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD.
∵∠A=30°,AC=2false,∴CD=false,∴BD=CD=false.
由勾股定理得:AD=false=3. ∴AB=AD+BD=3+false.
8. 解:如图,连结BC,则∠ACB=90°,△ECD∽△EBA,
∴false,cos∠CEB=false tan∠CEB=false
8题图
9. 解: (1)CD与⊙O相切.
理由:如图所示,连接OD,则∠AOD=2∠AED=2×45°=90°.
∵ 四边形ABCD是平行四边形,∴ AB∥DC,
∴ ∠CDO=∠AOD=90°,∴ OD⊥CD,∴CD与⊙O相切.
(2)如图所示,连接BE,则∠ADE=∠ABE.
∵AB是⊙O的直径,∴∠AEB=90°,AB=2×3=6(cm).
在Rt△ABE中,false.
∴sin∠ADE=sin∠ABEfalse.
9题图
拓展探究
1.探究:过点B作BD⊥AC,垂足为D.
∵AB=c,∠A=α,∴BD=c·sinα. ∴S△ABC=falseAC·BD=falsebcsinα.
应用:过点C作CE⊥DO于点E. ∴sinα=false.
∵在□ABCD中,AC=a,BD=b,∴CO=falsea,DO=falseb.
∴S△COD=falseCO·DO·sinα=18absinα.
∴S△BCD=falseCE×BD=false×falseasinα×b=falseabsinα,
∴S□ABCD=2S△BCD=falseabsinα.
