28.2.2应用举例(第2课时) 课堂互动训练(含答案)
文档属性
| 名称 | 28.2.2应用举例(第2课时) 课堂互动训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 476.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 15:17:09 | ||
图片预览



文档简介
28.2 .2应用举例(第2课时)
自主预习
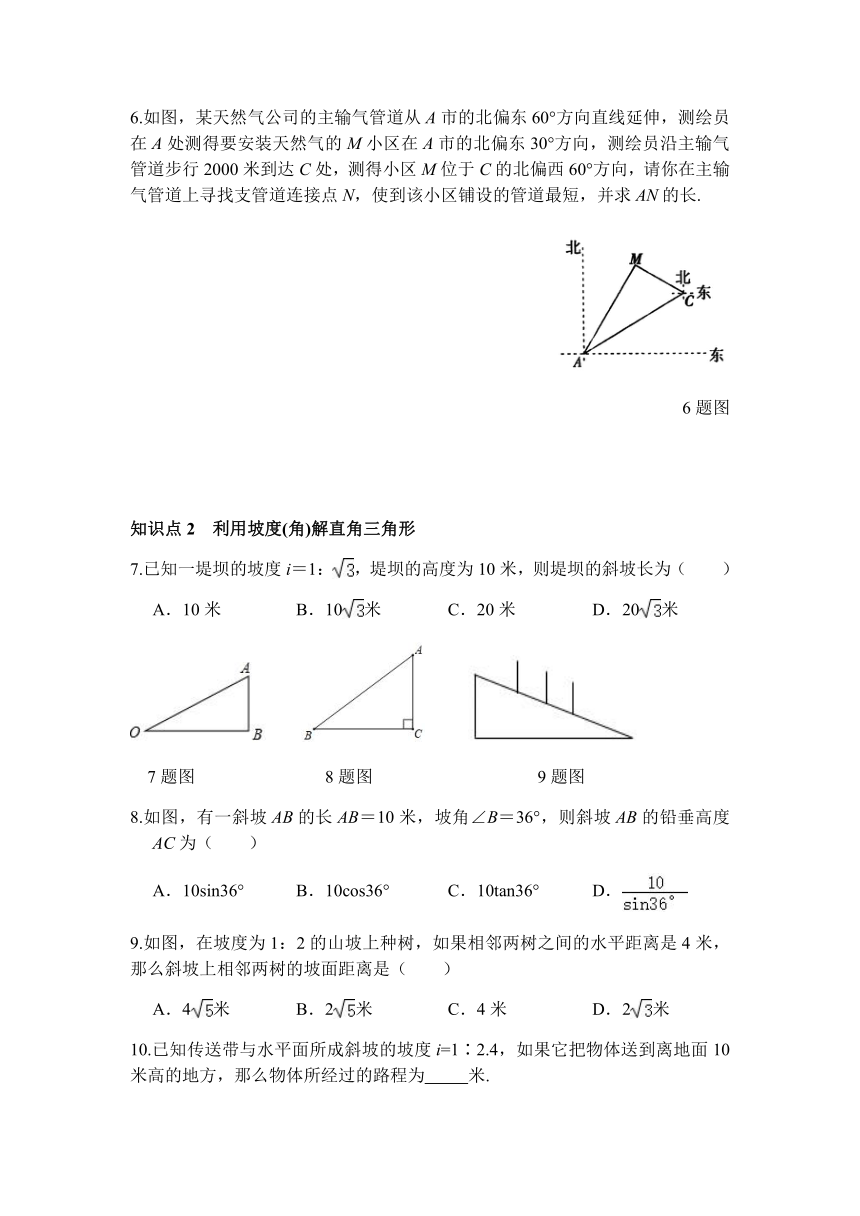
1. 如图,某人从O点沿北偏东30°的方向走了20米到达A点,B在O点的正东方,且在A的正南方,则此时AB间的距离是 米.(结果保留根号)
1题图 3题图
2. 坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的 (或坡比),记作i,即 .坡面与水平面的夹角叫做 ,记作tanα,有i=false= .
3. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1∶,则AB的长为( )
A.12米 B.4米 C.5米 D.6米
互动训练
知识点1 利用方向角解直角三角形
1. 小刚同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时小刚同学离A地( )
A.50falsem B.100 m C.150 m D.100false m
1题图 2题图 3题图
2.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
A.60海里 B.45海里 C.20false海里 D.30false海里
3.如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )
A.20(false+1)米/秒 B.20(false-1)米/秒 C.200米/秒 D.300米/秒
4. 如图所示,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求此时轮船所在的B处与灯塔P的距离(结果保留根号).
4题图
5. 如图,一海伦位于灯塔P的西南方向,距离灯塔40海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).
5题图
6.如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求AN的长.
6题图
知识点2 利用坡度(角)解直角三角形
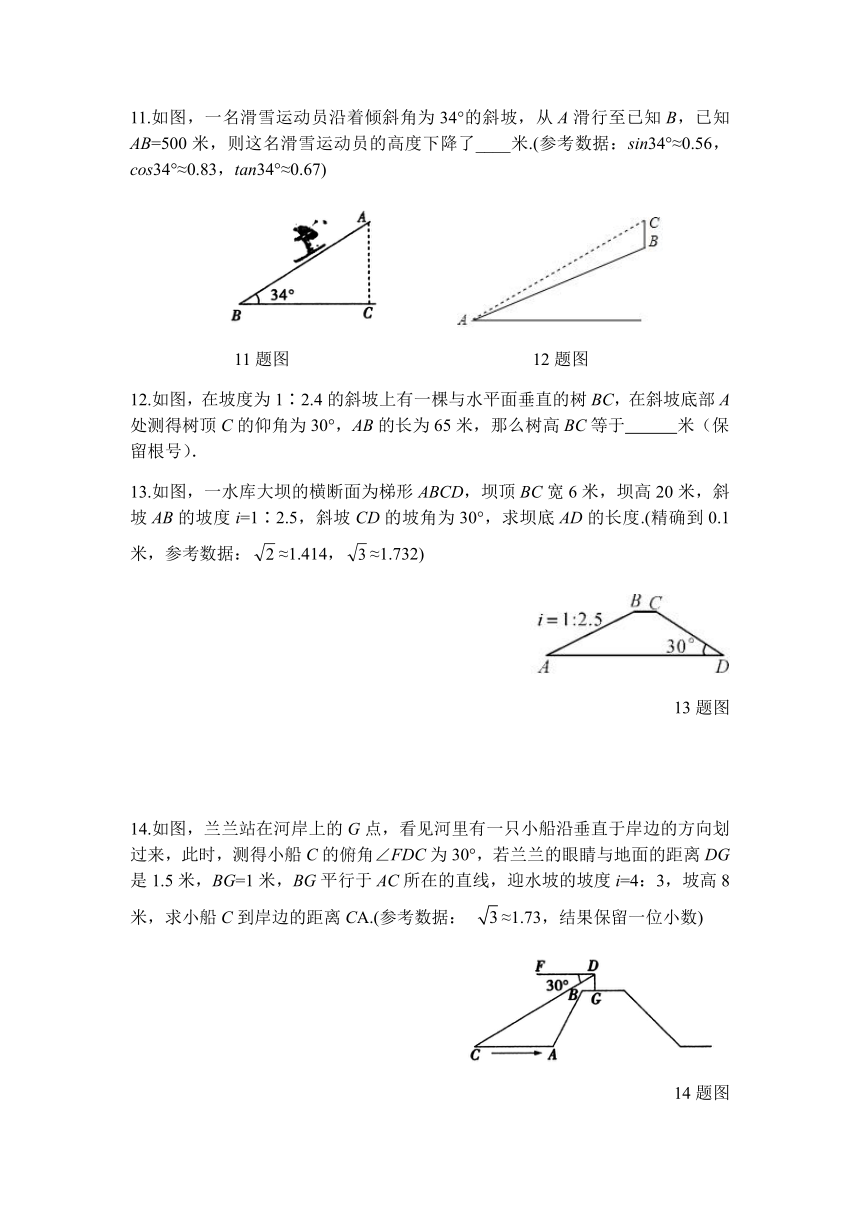
7.已知一堤坝的坡度i=1:,堤坝的高度为10米,则堤坝的斜坡长为( )
A.10米 B.10米 C.20米 D.20米
7题图 8题图 9题图
8.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10sin36° B.10cos36° C.10tan36° D.
9.如图,在坡度为1:2的山坡上种树,如果相邻两树之间的水平距离是4米,那么斜坡上相邻两树的坡面距离是( )
A.4米 B.2米 C.4米 D.2米
10.已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 米.
11.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至已知B,已知AB=500米,则这名滑雪运动员的高度下降了____米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
11题图 12题图
12.如图,在坡度为1∶2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30°,AB的长为65米,那么树高BC等于 米(保留根号).
13.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:false≈1.414,false≈1.732)
13题图
14.如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角∠FDC为30°,若兰兰的眼睛与地面的距离DG是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高8米,求小船C到岸边的距离CA.(参考数据: false≈1.73,结果保留一位小数)
14题图
15. 如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C在同一水平地面上.
(1)改善后斜坡坡面AD比原斜坡坡面AB会加长多少米?(精确到0.01)
(2)若斜坡的正前方能有3米长的空地就能保证安全,已知原斜坡AB的前方有6米长的空地,进行这样的改造是否可行?说明理由.
(参考数据:)
15题图
课时达标
1.如图,一艘船向东航行,上午8时到达A处,测得一灯塔B在船的北偏东30°方向,且距离船48海里;上午11时到达C处,测得灯塔在船的正北方向.则这艘船航行的速度为( )
A.24海里/时 B.8海里/时 C.24海里/时 D.8海里/时
1题图 2题图
2.一人乘雪橇沿坡比1:的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2,若滑到坡底的时间为4s,则此人下降的高度为( )
A.16m B.32m C.32m D.64m
3.如果某人沿坡度为3:4的斜坡前进10m,那么他所在的位置比原来的位置升高了( )
A.6m B.8m C.10m D.12m
4.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是 海里.
4题图 5题图
5.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1︰2.5,那么该斜坡的水平距离AC的长为 m.
6.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD,已知迎水坡面AB=12米,背水坡面CD=12false米,∠B=60°.加固后拦水坝的横断面为梯形ABED,tanE=false,则CE的长为 米.
6题图 7题图
7.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来,在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是 米.
8.一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
8题图
9.如图,一楼房AB后有一假山,其坡度为i=1∶false,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
9题图
拓展探究
1.四边形的两条对角线AC、BD所成的锐角为45°,当AC+BD=9时,四边形ABCD的面积最大值是( )
A. B. C.19 D.21
1题图 2题图
2.如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为 nmile.(结果保留根号)
3.某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)在图中直接标出表示60°和45°的角;
(2)写出点B、点C坐标;
(3)一辆汽车从点B匀速行驶到点C所用时间为15s.请你通过计算,判断该汽车在这段限速路上是否超速?(本小问中取1.7)
3题图
28.2.2应用举例(第2课时)答案
自主预习
1. 10false. 2. 坡度 i=false 坡角 tanα 3. A.
互动训练
1. D.
2. D. 解析:由题意知∠APB=90°,∠A=60°,PA=30海里,∴PB=PA·tanA=30×tan60°=30false(海里).故选D.
3. A. 解析:如图,过点B作BD⊥AC于点D.
在Rt△ABD中,因为∠ABD=60°,BD=200米,所以AD=BDtan∠ABD=200米,在Rt△CDB中,BD=200米,∠CBD=45°,所以CD=BD=200米,
则AC=AD+CD=(200+200false)米,
则平均速度是false=(20false+1)米/秒.故选A.
3题图 4题图
4. 解:过点P作PC⊥AB垂足为C,则∠APC=30°,∠BPC=45°,AP=80,
在Rt△APC中,.∴PC=PA·cos∠APC=,
在Rt△PCB中,,∴
∴当轮船位于灯塔P南偏东45°方向时,轮船与灯塔P的距离是海里.
5. 解:过P作PC⊥AB于点C,
在Rt△ACP中,PA=40海里,∠APC=45°,sin∠APC=,cos∠APC=,
∴AC=AP?sin45°=40×=40(海里),PC=AP?cos45°=40×=40(海里),
在Rt△BCP中,∠BPC=60°,tan∠BPC=,
∴BC=PC?tan60°=40(海里),
则AB=AC+BC=(40+40)海里.
5题图 6题图
6. 解:如图,过点M作MN⊥AC于点N,此时MN最短.
由题意知∠EAC=60°,∠EAM=30°,∴∠CAM=30°,
∴∠FCM=60°,∴∠MCB=30°,
∵∠EAC=60°,∴∠CAD=30°,∴∠BCA=30°,
∴∠MCA=∠MCB+∠BCA=60°,∴∠AMC=90°.
在Rt△AMC中,∠AMC=90°,∠MAC=30°,∴MC=falseAC=1000米.
在Rt△CMN中,∠MCN=60°,∴∠CMN=30°,∴NC=falseMC=500米.
∴AN=AC-NC=2000-500=1500(米).
因此,AN的长为1500米.
7. C. 解析:如图所示,∵山路坡面坡度i=1︰false,
∴设AB=x,则OB=falsex,∴OA=2x.
∵堤坝的高度为10米,∴AB=10米,∴OA=20米.故选:C.
7题图 8题图 9题图
8. A. 解析:由题意知:sinB=,即sin36°=,故AC=10sin36°.故选:A.
9. B. 解析:如图,在Rt△ABC中,=
∵AC=4,∴BC=2,由勾股定理得,AB==2(米),故选:B.
10. 26
11.280. 解析:在Rt△ABC中,AC=ABsin34°=500×0.56≈280(米),
所以这名滑雪运动员的高度下降了280米.
12. (20﹣25).解析:如图,延长CB交水平面于点D,
根据题意可知:CD⊥AD,∴∠ADC=90°,
在Rt△ADB中,AB=65,
∵BD︰AD=1︰2.4,∴AD=2.4BD,根据勾股定理,
得AD2+BD2=AB2,即BD2+(2.4BD)2=652,解得BD=25,∴AD=60,
在Rt△ACD中,∠CAD=30°,
∴tan30°=,即=,解得CB=20﹣25(米).
答:树高BC等于(20﹣25)米.故答案为:(20﹣25).
12题图 14题图
13.解:作BE⊥AD,CF⊥AD,垂足分别为点E,F,则四边形BCFE是矩形.
由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1∶2.5,
在Rt△ABE中,BE=20米,false=false,∴AE=50米.
在Rt△CFD中,∠D=30°,∴DF=false=20false米.
∴AD=AE+EF+FD=50+6+20false≈90.6(米).
答:坝底AD的长度约为90.6米.
14.解:如图,过点B作BE⊥CA交CA的延长线于点E,延长DG交CA的延长线于点H,得Rt△ABE和矩形BEHG.
∵i=false=false,BE=8米,∴AE=6米.
∵DG=1.5米,BG=l米,
∴DH=DG+GH=1.5+8=9.5(米),AH=AE+EH=6+l=7(米).
在Rt△CDH中,∵∠C=∠FDC=30°,DH=9.5米,tanC=false,∴CH=false米.
又CH=CA+7,即false=CA+7,∴CA≈9.4米.
因此,小船C到岸边的距离CA约是9.4米.
15. 解:(1)在Rt△ABC中,
BC=AC=AB?sin45°=(m),
在Rt△ADC中,AD==5(m),
CD==(m),∴AD﹣AB≈2.07(m).
改善后的斜坡会加长2.07m;
(2)这样改造能行.
∵CD﹣BC ≈2.59(m),而6﹣3>2.59,∴这样改造能行.
15题图
课时达标
1. D. 解析:在Rt△ABC中,∵∠B=30°,AB=48海里,∴AC=AB=24海里,
则这艘船航行的速度为24÷3=8(海里/小时), 故选:D.
2. B. 解析:设斜坡的坡角为α,当t=4时,s=8×4+2×42=64,
∵斜坡的坡比1:,∴tanα=,∴α=30°,
∴此人下降的高度=×64=32(m),故选:B.
3. A. 解析:设他所在的位置比原来的位置升高了3xm,
∵坡度为3:4,∴他前进的水平距离为4xm,
由勾股定理得,(3x)2+(4x)2=102,解得,x=2,
则3x=6,即他所在的位置比原来的位置升高了6m,故选:A.
4. 40. 解析:如图所示:由题意可得,∠PAB=30°,∠DBP=30°,
∴∠PBE=60°,∴∠P=∠PAB=30°,∴AB=BP=40海里.故答案为:40.
4题图 6题图
5. 75. 解析:∵斜坡的坡度i=1︰2.5,∴BC︰AC=1︰2.5,∴AC=75(m),
故答案为:75.
6. 8. 解析:如图,分别过点A,D作AF⊥BC,DG⊥BC,垂足分别为F,G.
在Rt△ABF中,AB=12米,∠B=60°,sinB=false,
∴AF=false米,∴DG=false米,
在Rt△DGC中,∵CD=12false米,DG=false米,
∴GC=false =18米.
在Rt△DEG中,∵tanE=false,∴false,
∴GE =26米,∴CE=GE-CG=26-18=8(米),即CE的长为8米.
7. 15﹣5).解:如图,过点B作BH⊥AE于点H,BF⊥CE于点F,
根据题意可知:∠BAH=30°,AB=AE=10,∴BH=5,AH=5,
∵CE⊥AE,∴四边形BHEF是矩形,∴EF=BH=5,
BF=HE=AH+AE=5+10,
∵∠DAE=60°,∴DE=AE?tan60°=10,∴DF=DE﹣EF=10﹣5,
∵∠CBF=45°,∴CF=BF=5+10,
∴CD=CF﹣DF=5+10﹣(10﹣5)=15﹣5(米).
所以标识牌CD的高度是(15﹣5)米.故答案为:(15﹣5).
7题图
8.过点C作CD⊥AB,交AB的延长线于点D.
由题意,得∠CAD=30°,∠CBD=53°,AC=80海里,∴CD=40海里.
在Rt△CBD中,sin53°=false,
∴CB=false≈false=50(海里).false=1.25(小时).
答:海警船到达C处需1.25小时.
9.过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,∵i=false=false=tan∠ECF,∴∠ECF=30°.
∴EF=falseCE=10米,CF=10false米.
∴BH=EF=10米,HE=BF=BC+CF=(25+10false)米.
在Rt△AHE中,∵∠HAE=45°,∴AH=HE=(25+10false)米.
∴AB=AH+HB=(35+10false)米.
答:楼房AB的高为(35+10false)米.
拓展探究
1. B. 解析:过B作BF⊥AC,与CA延长线交于点F,过D作DE⊥AC于点E,
∵AC与BD所成的锐角为45°,∴BF=OBsin45°,DE=ODsin45°,
∴四边形ABCD的面积=
S△ABC+S△ACD=falseAC·BF+falseAC·DE=falseAC(BF+DE)
=falseAC(OBsin45°+ODsin45°)=falseAC·BD·sin45°
设AC=x,则BD=9﹣x,
∴S=x(9﹣x)×=﹣(x﹣)2+,
∴当x=,S有最大值. 故选:B.
1题图
2. 50.解析:根据题意,得:∠PAB=60°,∠PBA=30,AB=2.5×40=100(nmile),
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣60°﹣30°=90°.
在Rt△PAB中,PB=AB?sin∠PAB=100×=50(nmile).
故答案为:50.
3. 解:(1)如图所示,∠OAB=60°,∠OAC=45°;
(2)∵在直角三角形ABO中,AO=100,∠BAO=60度,
∴OB=OA?tan60°=100,∴点B的坐标是(﹣100,0);
∵△AOC是等腰直角三角形,∴OC=OA=100,
∴C的坐标是(100,0);
(3)BC=BO+OC=100+100≈270(m).270÷15=18(m/s).
∵18>,∴该汽车在这段限速路上超速了.
3题图
自主预习
1. 如图,某人从O点沿北偏东30°的方向走了20米到达A点,B在O点的正东方,且在A的正南方,则此时AB间的距离是 米.(结果保留根号)
1题图 3题图
2. 坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的 (或坡比),记作i,即 .坡面与水平面的夹角叫做 ,记作tanα,有i=false= .
3. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1∶,则AB的长为( )
A.12米 B.4米 C.5米 D.6米
互动训练
知识点1 利用方向角解直角三角形
1. 小刚同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时小刚同学离A地( )
A.50falsem B.100 m C.150 m D.100false m
1题图 2题图 3题图
2.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
A.60海里 B.45海里 C.20false海里 D.30false海里
3.如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )
A.20(false+1)米/秒 B.20(false-1)米/秒 C.200米/秒 D.300米/秒
4. 如图所示,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求此时轮船所在的B处与灯塔P的距离(结果保留根号).
4题图
5. 如图,一海伦位于灯塔P的西南方向,距离灯塔40海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).
5题图
6.如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求AN的长.
6题图
知识点2 利用坡度(角)解直角三角形
7.已知一堤坝的坡度i=1:,堤坝的高度为10米,则堤坝的斜坡长为( )
A.10米 B.10米 C.20米 D.20米
7题图 8题图 9题图
8.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10sin36° B.10cos36° C.10tan36° D.
9.如图,在坡度为1:2的山坡上种树,如果相邻两树之间的水平距离是4米,那么斜坡上相邻两树的坡面距离是( )
A.4米 B.2米 C.4米 D.2米
10.已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 米.
11.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至已知B,已知AB=500米,则这名滑雪运动员的高度下降了____米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
11题图 12题图
12.如图,在坡度为1∶2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30°,AB的长为65米,那么树高BC等于 米(保留根号).
13.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:false≈1.414,false≈1.732)
13题图
14.如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角∠FDC为30°,若兰兰的眼睛与地面的距离DG是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高8米,求小船C到岸边的距离CA.(参考数据: false≈1.73,结果保留一位小数)
14题图
15. 如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C在同一水平地面上.
(1)改善后斜坡坡面AD比原斜坡坡面AB会加长多少米?(精确到0.01)
(2)若斜坡的正前方能有3米长的空地就能保证安全,已知原斜坡AB的前方有6米长的空地,进行这样的改造是否可行?说明理由.
(参考数据:)
15题图
课时达标
1.如图,一艘船向东航行,上午8时到达A处,测得一灯塔B在船的北偏东30°方向,且距离船48海里;上午11时到达C处,测得灯塔在船的正北方向.则这艘船航行的速度为( )
A.24海里/时 B.8海里/时 C.24海里/时 D.8海里/时
1题图 2题图
2.一人乘雪橇沿坡比1:的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2,若滑到坡底的时间为4s,则此人下降的高度为( )
A.16m B.32m C.32m D.64m
3.如果某人沿坡度为3:4的斜坡前进10m,那么他所在的位置比原来的位置升高了( )
A.6m B.8m C.10m D.12m
4.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是 海里.
4题图 5题图
5.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1︰2.5,那么该斜坡的水平距离AC的长为 m.
6.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD,已知迎水坡面AB=12米,背水坡面CD=12false米,∠B=60°.加固后拦水坝的横断面为梯形ABED,tanE=false,则CE的长为 米.
6题图 7题图
7.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来,在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是 米.
8.一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
8题图
9.如图,一楼房AB后有一假山,其坡度为i=1∶false,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
9题图
拓展探究
1.四边形的两条对角线AC、BD所成的锐角为45°,当AC+BD=9时,四边形ABCD的面积最大值是( )
A. B. C.19 D.21
1题图 2题图
2.如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为 nmile.(结果保留根号)
3.某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)在图中直接标出表示60°和45°的角;
(2)写出点B、点C坐标;
(3)一辆汽车从点B匀速行驶到点C所用时间为15s.请你通过计算,判断该汽车在这段限速路上是否超速?(本小问中取1.7)
3题图
28.2.2应用举例(第2课时)答案
自主预习
1. 10false. 2. 坡度 i=false 坡角 tanα 3. A.
互动训练
1. D.
2. D. 解析:由题意知∠APB=90°,∠A=60°,PA=30海里,∴PB=PA·tanA=30×tan60°=30false(海里).故选D.
3. A. 解析:如图,过点B作BD⊥AC于点D.
在Rt△ABD中,因为∠ABD=60°,BD=200米,所以AD=BDtan∠ABD=200米,在Rt△CDB中,BD=200米,∠CBD=45°,所以CD=BD=200米,
则AC=AD+CD=(200+200false)米,
则平均速度是false=(20false+1)米/秒.故选A.
3题图 4题图
4. 解:过点P作PC⊥AB垂足为C,则∠APC=30°,∠BPC=45°,AP=80,
在Rt△APC中,.∴PC=PA·cos∠APC=,
在Rt△PCB中,,∴
∴当轮船位于灯塔P南偏东45°方向时,轮船与灯塔P的距离是海里.
5. 解:过P作PC⊥AB于点C,
在Rt△ACP中,PA=40海里,∠APC=45°,sin∠APC=,cos∠APC=,
∴AC=AP?sin45°=40×=40(海里),PC=AP?cos45°=40×=40(海里),
在Rt△BCP中,∠BPC=60°,tan∠BPC=,
∴BC=PC?tan60°=40(海里),
则AB=AC+BC=(40+40)海里.
5题图 6题图
6. 解:如图,过点M作MN⊥AC于点N,此时MN最短.
由题意知∠EAC=60°,∠EAM=30°,∴∠CAM=30°,
∴∠FCM=60°,∴∠MCB=30°,
∵∠EAC=60°,∴∠CAD=30°,∴∠BCA=30°,
∴∠MCA=∠MCB+∠BCA=60°,∴∠AMC=90°.
在Rt△AMC中,∠AMC=90°,∠MAC=30°,∴MC=falseAC=1000米.
在Rt△CMN中,∠MCN=60°,∴∠CMN=30°,∴NC=falseMC=500米.
∴AN=AC-NC=2000-500=1500(米).
因此,AN的长为1500米.
7. C. 解析:如图所示,∵山路坡面坡度i=1︰false,
∴设AB=x,则OB=falsex,∴OA=2x.
∵堤坝的高度为10米,∴AB=10米,∴OA=20米.故选:C.
7题图 8题图 9题图
8. A. 解析:由题意知:sinB=,即sin36°=,故AC=10sin36°.故选:A.
9. B. 解析:如图,在Rt△ABC中,=
∵AC=4,∴BC=2,由勾股定理得,AB==2(米),故选:B.
10. 26
11.280. 解析:在Rt△ABC中,AC=ABsin34°=500×0.56≈280(米),
所以这名滑雪运动员的高度下降了280米.
12. (20﹣25).解析:如图,延长CB交水平面于点D,
根据题意可知:CD⊥AD,∴∠ADC=90°,
在Rt△ADB中,AB=65,
∵BD︰AD=1︰2.4,∴AD=2.4BD,根据勾股定理,
得AD2+BD2=AB2,即BD2+(2.4BD)2=652,解得BD=25,∴AD=60,
在Rt△ACD中,∠CAD=30°,
∴tan30°=,即=,解得CB=20﹣25(米).
答:树高BC等于(20﹣25)米.故答案为:(20﹣25).
12题图 14题图
13.解:作BE⊥AD,CF⊥AD,垂足分别为点E,F,则四边形BCFE是矩形.
由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1∶2.5,
在Rt△ABE中,BE=20米,false=false,∴AE=50米.
在Rt△CFD中,∠D=30°,∴DF=false=20false米.
∴AD=AE+EF+FD=50+6+20false≈90.6(米).
答:坝底AD的长度约为90.6米.
14.解:如图,过点B作BE⊥CA交CA的延长线于点E,延长DG交CA的延长线于点H,得Rt△ABE和矩形BEHG.
∵i=false=false,BE=8米,∴AE=6米.
∵DG=1.5米,BG=l米,
∴DH=DG+GH=1.5+8=9.5(米),AH=AE+EH=6+l=7(米).
在Rt△CDH中,∵∠C=∠FDC=30°,DH=9.5米,tanC=false,∴CH=false米.
又CH=CA+7,即false=CA+7,∴CA≈9.4米.
因此,小船C到岸边的距离CA约是9.4米.
15. 解:(1)在Rt△ABC中,
BC=AC=AB?sin45°=(m),
在Rt△ADC中,AD==5(m),
CD==(m),∴AD﹣AB≈2.07(m).
改善后的斜坡会加长2.07m;
(2)这样改造能行.
∵CD﹣BC ≈2.59(m),而6﹣3>2.59,∴这样改造能行.
15题图
课时达标
1. D. 解析:在Rt△ABC中,∵∠B=30°,AB=48海里,∴AC=AB=24海里,
则这艘船航行的速度为24÷3=8(海里/小时), 故选:D.
2. B. 解析:设斜坡的坡角为α,当t=4时,s=8×4+2×42=64,
∵斜坡的坡比1:,∴tanα=,∴α=30°,
∴此人下降的高度=×64=32(m),故选:B.
3. A. 解析:设他所在的位置比原来的位置升高了3xm,
∵坡度为3:4,∴他前进的水平距离为4xm,
由勾股定理得,(3x)2+(4x)2=102,解得,x=2,
则3x=6,即他所在的位置比原来的位置升高了6m,故选:A.
4. 40. 解析:如图所示:由题意可得,∠PAB=30°,∠DBP=30°,
∴∠PBE=60°,∴∠P=∠PAB=30°,∴AB=BP=40海里.故答案为:40.
4题图 6题图
5. 75. 解析:∵斜坡的坡度i=1︰2.5,∴BC︰AC=1︰2.5,∴AC=75(m),
故答案为:75.
6. 8. 解析:如图,分别过点A,D作AF⊥BC,DG⊥BC,垂足分别为F,G.
在Rt△ABF中,AB=12米,∠B=60°,sinB=false,
∴AF=false米,∴DG=false米,
在Rt△DGC中,∵CD=12false米,DG=false米,
∴GC=false =18米.
在Rt△DEG中,∵tanE=false,∴false,
∴GE =26米,∴CE=GE-CG=26-18=8(米),即CE的长为8米.
7. 15﹣5).解:如图,过点B作BH⊥AE于点H,BF⊥CE于点F,
根据题意可知:∠BAH=30°,AB=AE=10,∴BH=5,AH=5,
∵CE⊥AE,∴四边形BHEF是矩形,∴EF=BH=5,
BF=HE=AH+AE=5+10,
∵∠DAE=60°,∴DE=AE?tan60°=10,∴DF=DE﹣EF=10﹣5,
∵∠CBF=45°,∴CF=BF=5+10,
∴CD=CF﹣DF=5+10﹣(10﹣5)=15﹣5(米).
所以标识牌CD的高度是(15﹣5)米.故答案为:(15﹣5).
7题图
8.过点C作CD⊥AB,交AB的延长线于点D.
由题意,得∠CAD=30°,∠CBD=53°,AC=80海里,∴CD=40海里.
在Rt△CBD中,sin53°=false,
∴CB=false≈false=50(海里).false=1.25(小时).
答:海警船到达C处需1.25小时.
9.过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,∵i=false=false=tan∠ECF,∴∠ECF=30°.
∴EF=falseCE=10米,CF=10false米.
∴BH=EF=10米,HE=BF=BC+CF=(25+10false)米.
在Rt△AHE中,∵∠HAE=45°,∴AH=HE=(25+10false)米.
∴AB=AH+HB=(35+10false)米.
答:楼房AB的高为(35+10false)米.
拓展探究
1. B. 解析:过B作BF⊥AC,与CA延长线交于点F,过D作DE⊥AC于点E,
∵AC与BD所成的锐角为45°,∴BF=OBsin45°,DE=ODsin45°,
∴四边形ABCD的面积=
S△ABC+S△ACD=falseAC·BF+falseAC·DE=falseAC(BF+DE)
=falseAC(OBsin45°+ODsin45°)=falseAC·BD·sin45°
设AC=x,则BD=9﹣x,
∴S=x(9﹣x)×=﹣(x﹣)2+,
∴当x=,S有最大值. 故选:B.
1题图
2. 50.解析:根据题意,得:∠PAB=60°,∠PBA=30,AB=2.5×40=100(nmile),
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣60°﹣30°=90°.
在Rt△PAB中,PB=AB?sin∠PAB=100×=50(nmile).
故答案为:50.
3. 解:(1)如图所示,∠OAB=60°,∠OAC=45°;
(2)∵在直角三角形ABO中,AO=100,∠BAO=60度,
∴OB=OA?tan60°=100,∴点B的坐标是(﹣100,0);
∵△AOC是等腰直角三角形,∴OC=OA=100,
∴C的坐标是(100,0);
(3)BC=BO+OC=100+100≈270(m).270÷15=18(m/s).
∵18>,∴该汽车在这段限速路上超速了.
3题图
