七年级数学一对一教案--相交线与平行线1
文档属性
| 名称 | 七年级数学一对一教案--相交线与平行线1 |  | |
| 格式 | zip | ||
| 文件大小 | 25.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-15 19:18:06 | ||
图片预览


文档简介
姓名 年级 七 性别 总课时____第___课
教学目标 知识点:考点:能力:方法:
难点重点
课堂教学过程 课前检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
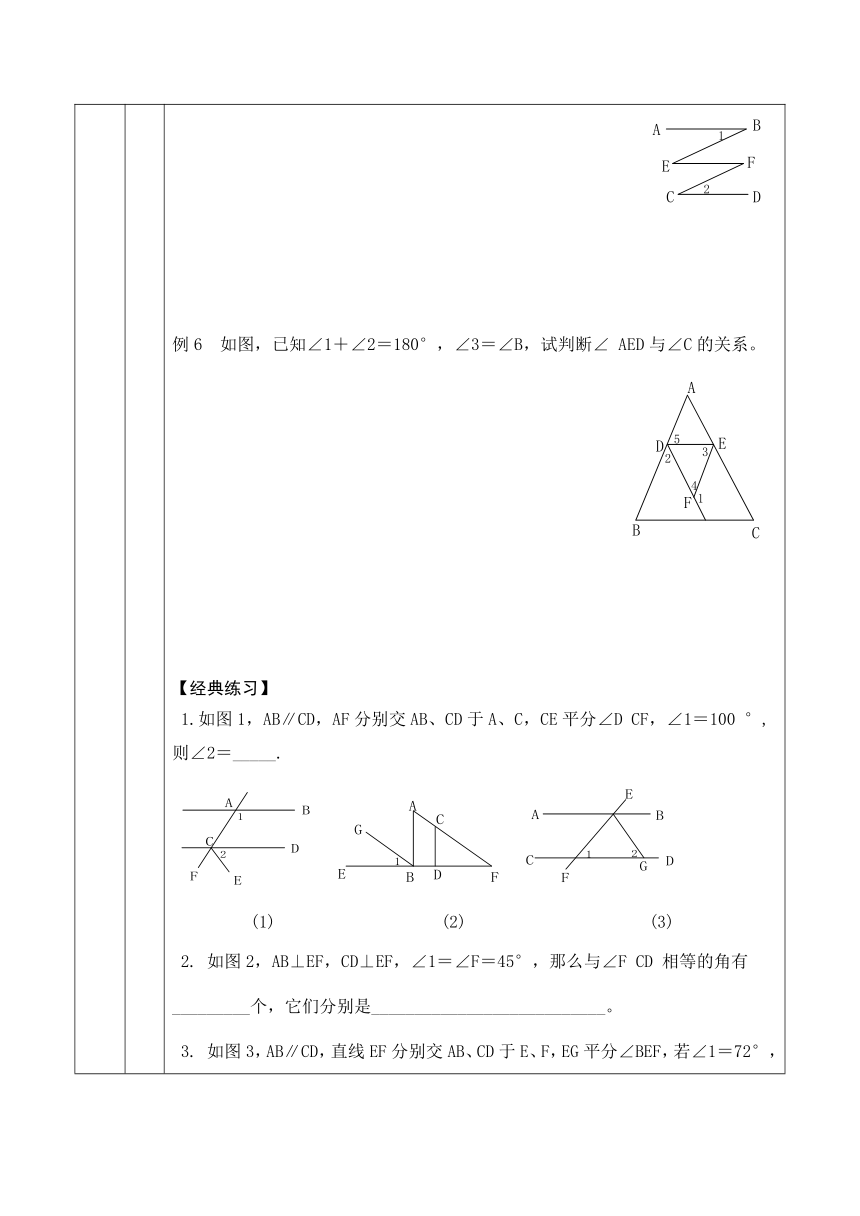
过程 平行线与相交线(一)【知识要点】1.余角----如果两个角的和是直角,那么称这两个角互为余角。补角----如果两个角的和是平角,那么称这两个角互为补角。性质:同角或等角的余角相等;同角或等角的补角相等.2.对顶角和邻补角:两条直线相交所成的4个角中,相邻的两个角是邻补角,不相邻的角的对顶角,如图中∠1和∠2是邻补角,∠1和∠3是对顶角.性质:(1)邻补角互补(互补角的一种特殊情况).(2)对顶角相等.3. 两条直线互相垂直,垂线、垂足的定义,垂线的性质:a.同一平面内,过一点有且只有一条直线与已知直线垂直.b.直线外一点与直线上各点连结的所有线段中,垂线段最短.4. 平行线的性质:a.两直线没有交点. b.过直线外一点仅有一条直线与已知直线平行. (1)两直线平行, 同位角相等. (2)两直线平行, 内错角相等. (3)两直线平行, 同旁内角互补.【典型例题】已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数。例2 如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME 的度数。 例3 如图,DE∥CB,试证明∠AED=∠A+∠B。例4 如图,AB∥CD,∠1=∠2,∠BEF与 ∠EFC相等吗?为什么? 例6 如图,已知∠1+∠2=180°,∠3=∠B,试判断∠ AED与∠C的关系。【经典练习】1.如图1,AB∥CD,AF分别交AB、CD于A、C,CE平分∠D CF,∠1=100 °,则∠2=_____.毛 (1) (2) (3)2. 如图2,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠F CD 相等的角有_________个,它们分别是___________________________。3. 如图3,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=_________。4.如图4,若∠1=∠2,∠3=73 ,则∠4= .5. 如图5,BD是一条直线,CE∥AB,则∠1= ,∠2= ,又因为∠1+∠2+∠ACB=180 , 故∠A+∠B+∠ACB= .6.如图6,若∠1=80 ,a∥b,则∠2的度数是( ) A.100 B.70 C.80 D.60 图4图5 图6图77. 下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行④两直线平行,同位角相等,其中是平行线特征的是( ) A.① B.②③ C.④ D.①④8. 如图7,AC∥BD,AE∥BF,下列结论错误的是( )A. ∠A=∠B B. ∠A=∠1 C. ∠B=∠2 D. ∠A+∠B=180 9.下列说法错误的是( ) A.在同一平面内,垂直于同一直线的两直线平行B.两条直线被第三条直线所截,同旁内角互补C.平行于同一直线的两条直线平行D.若两条平行线被第三条直线所截,一组同旁内角的角平分线互相垂直10.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )A.相等 B.互补 C.相等或互补 D.相等且互补11.下列说法中,为平行线特征的是( ) ①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A.① B.②③ C.④ D.②和④12.如图8,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=( )A.60° B.50° C.30° D.20° (8) (9)13. 如图9,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关————教学具体内容要有提示或附后
课堂检测 听课及知识掌握情况反馈_________________________________________________________。测试题(累计不超过20分钟)_______道;成绩_______;教学需:加快□;保持□;放慢□;增加内容□
课后巩固 作业_____题; 巩固复习____________________ ; 预习布置_____________________
签字 教学组长签字: 学习管理师:
老师课后赏识评价 老师最欣赏的地方:
老师想知道的事情:
老师的建议:
1
2
3
a
b
O
教学目标 知识点:考点:能力:方法:
难点重点
课堂教学过程 课前检查 作业完成情况:优□ 良□ 中□ 差□ 建议__________________________________________
过程 平行线与相交线(一)【知识要点】1.余角----如果两个角的和是直角,那么称这两个角互为余角。补角----如果两个角的和是平角,那么称这两个角互为补角。性质:同角或等角的余角相等;同角或等角的补角相等.2.对顶角和邻补角:两条直线相交所成的4个角中,相邻的两个角是邻补角,不相邻的角的对顶角,如图中∠1和∠2是邻补角,∠1和∠3是对顶角.性质:(1)邻补角互补(互补角的一种特殊情况).(2)对顶角相等.3. 两条直线互相垂直,垂线、垂足的定义,垂线的性质:a.同一平面内,过一点有且只有一条直线与已知直线垂直.b.直线外一点与直线上各点连结的所有线段中,垂线段最短.4. 平行线的性质:a.两直线没有交点. b.过直线外一点仅有一条直线与已知直线平行. (1)两直线平行, 同位角相等. (2)两直线平行, 内错角相等. (3)两直线平行, 同旁内角互补.【典型例题】已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数。例2 如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME 的度数。 例3 如图,DE∥CB,试证明∠AED=∠A+∠B。例4 如图,AB∥CD,∠1=∠2,∠BEF与 ∠EFC相等吗?为什么? 例6 如图,已知∠1+∠2=180°,∠3=∠B,试判断∠ AED与∠C的关系。【经典练习】1.如图1,AB∥CD,AF分别交AB、CD于A、C,CE平分∠D CF,∠1=100 °,则∠2=_____.毛 (1) (2) (3)2. 如图2,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠F CD 相等的角有_________个,它们分别是___________________________。3. 如图3,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=_________。4.如图4,若∠1=∠2,∠3=73 ,则∠4= .5. 如图5,BD是一条直线,CE∥AB,则∠1= ,∠2= ,又因为∠1+∠2+∠ACB=180 , 故∠A+∠B+∠ACB= .6.如图6,若∠1=80 ,a∥b,则∠2的度数是( ) A.100 B.70 C.80 D.60 图4图5 图6图77. 下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行④两直线平行,同位角相等,其中是平行线特征的是( ) A.① B.②③ C.④ D.①④8. 如图7,AC∥BD,AE∥BF,下列结论错误的是( )A. ∠A=∠B B. ∠A=∠1 C. ∠B=∠2 D. ∠A+∠B=180 9.下列说法错误的是( ) A.在同一平面内,垂直于同一直线的两直线平行B.两条直线被第三条直线所截,同旁内角互补C.平行于同一直线的两条直线平行D.若两条平行线被第三条直线所截,一组同旁内角的角平分线互相垂直10.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )A.相等 B.互补 C.相等或互补 D.相等且互补11.下列说法中,为平行线特征的是( ) ①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A.① B.②③ C.④ D.②和④12.如图8,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=( )A.60° B.50° C.30° D.20° (8) (9)13. 如图9,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关————教学具体内容要有提示或附后
课堂检测 听课及知识掌握情况反馈_________________________________________________________。测试题(累计不超过20分钟)_______道;成绩_______;教学需:加快□;保持□;放慢□;增加内容□
课后巩固 作业_____题; 巩固复习____________________ ; 预习布置_____________________
签字 教学组长签字: 学习管理师:
老师课后赏识评价 老师最欣赏的地方:
老师想知道的事情:
老师的建议:
1
2
3
a
b
O
