沪教版(上海)数学九年级第二学期-27.4 直线和圆的位置关系 教案
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.4 直线和圆的位置关系 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 71.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览


文档简介
27.4直线和圆的位置关系
一、教学目标:
1、理解直线和圆的三种位置关系,并掌握其判定方法和性质;了解切线的判断定理.
2、通过直线和圆的位置关系的探究,渗透分类、数形结合的思想,培养观察、分析和概括的能力.
二、教学重点及难点:
直线和圆的位置关系的判定方法和性质.
三、教学用具准备:
学生每人准备一只铅笔、一只圆规、一把直尺.
四、教学过程:
(一)通过观察,引入新课
观察:请同学观察“海上日出”照片,地平线与太阳的位置关系是怎样的? 这个自然现象反映出直线和圆的位置关系有哪几种?
2286001342390l
l
l
(1)
(2)
(3)
O
O
O
l
l
l
(1)
(2)
(3)
O
O
O
(二)新课讲授
1、观察
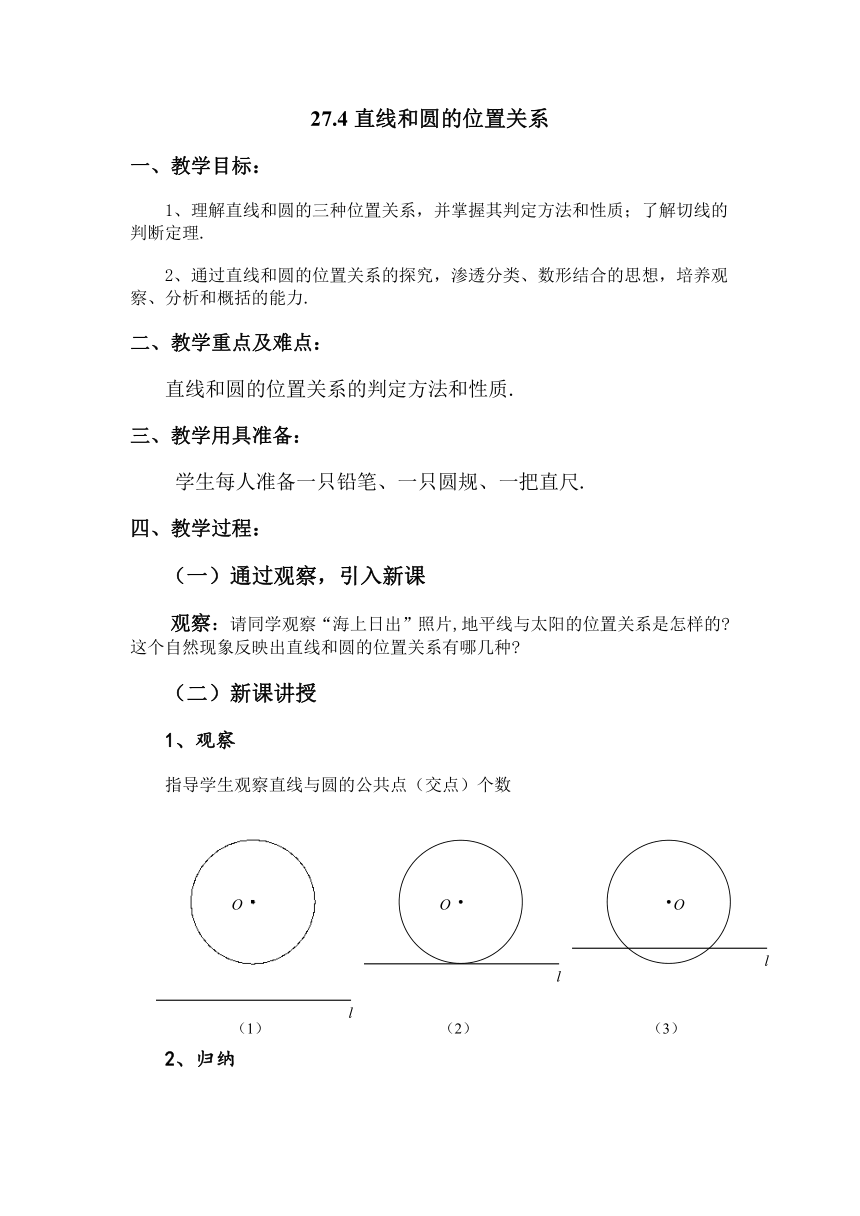
指导学生观察直线与圆的公共点(交点)个数
2、归纳
(1)直线和圆没有公共点;(2)直线和圆有唯一公共点;
(3)直线与圆有两个公共点.
3、概念
由直线与圆的公共点的个数,得出直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线.
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点.
(3)相离:直线和圆没有公共点时,叫做直线和圆相离.
4、理解
(1)直线与圆有唯一公共点的含义是“有且仅有”,这与直线与圆有一个公共点的含义不同处.
(2)直线和圆除了上述三种位置关系外,有第四种关系吗?即一条直线和圆的公共点能否多于两个?为什么?
5、直线与圆的位置关系的量化:
(1)迁移:点与圆的位置关系
(1)点P在⊙O内falsed (2)点P在⊙O上falsed=r;
(3)点P在⊙O外falsed>r.
4457700334010(2)做一做:
已知:O为直线l外一点,OT⊥l,且OT=d。请以O为圆心,分别以 为半径画圆.所画的圆与直线l有什么位置关系?
(3)如图:圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
●O
●O
相交
●O
相切
相离
●O
●O
相交
●O
相切
相离
(4)归纳概括:
如果⊙O的半径为r ,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交 falsed (2)直线l和⊙O相切 falsed=r;
(3)直线l和⊙O相离 falsed>r.
(5)练一练:
34290004997451.设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:
217170025400d=4,r=3 (2)d=1,r= (3)
5715000(4)
2.在直角三角形ABC 中, ∠ACB=90°,CA=3,CB=4.设⊙C 的半径为r. 请根据r的下列值,判断AB与⊙C 的位置关系,并说明理由.
(1) r=2 (2) r=2.4 (3) r=3
6、切线的判定定理
(1)分析d=r的几何表示,引出切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)证明定理.师生共同分析该定理的条件和结论,画出图形,写出已知、求证,指导学生完成证明.
7、例题讲解
3886200229870O
M
O
M
例1:经过⊙O上一点M作⊙O的切线.
作法:1、联结OM.
2、过点M作直线l垂直于OM.
则直线l就是所求作的切线.
(作图由学生自己完成)
例2:已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(三)巩固练习
1、如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)圆心为点C、半径长R为2的圆与直线AB有怎样的位置关系?
(2)圆心为点C、半径长R为4的圆与直线AB有怎样的位置关系?
(3)如果以点C为圆心的圆与直线AB有公共点,求⊙C的半径R的取值范围.
2、船有无触礁的危险?
海中有一个小岛P,该岛四周12海里内暗礁.今有货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行. 你认为货轮继续向东航行途中会有触礁的危险吗?
(四)课堂小结:
说说这节课的收获和体验,让大家一起分享!
(五)布置作业:习题27.4
一、教学目标:
1、理解直线和圆的三种位置关系,并掌握其判定方法和性质;了解切线的判断定理.
2、通过直线和圆的位置关系的探究,渗透分类、数形结合的思想,培养观察、分析和概括的能力.
二、教学重点及难点:
直线和圆的位置关系的判定方法和性质.
三、教学用具准备:
学生每人准备一只铅笔、一只圆规、一把直尺.
四、教学过程:
(一)通过观察,引入新课
观察:请同学观察“海上日出”照片,地平线与太阳的位置关系是怎样的? 这个自然现象反映出直线和圆的位置关系有哪几种?
2286001342390l
l
l
(1)
(2)
(3)
O
O
O
l
l
l
(1)
(2)
(3)
O
O
O
(二)新课讲授
1、观察
指导学生观察直线与圆的公共点(交点)个数
2、归纳
(1)直线和圆没有公共点;(2)直线和圆有唯一公共点;
(3)直线与圆有两个公共点.
3、概念
由直线与圆的公共点的个数,得出直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线.
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点.
(3)相离:直线和圆没有公共点时,叫做直线和圆相离.
4、理解
(1)直线与圆有唯一公共点的含义是“有且仅有”,这与直线与圆有一个公共点的含义不同处.
(2)直线和圆除了上述三种位置关系外,有第四种关系吗?即一条直线和圆的公共点能否多于两个?为什么?
5、直线与圆的位置关系的量化:
(1)迁移:点与圆的位置关系
(1)点P在⊙O内falsed
(3)点P在⊙O外falsed>r.
4457700334010(2)做一做:
已知:O为直线l外一点,OT⊥l,且OT=d。请以O为圆心,分别以 为半径画圆.所画的圆与直线l有什么位置关系?
(3)如图:圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
●O
●O
相交
●O
相切
相离
●O
●O
相交
●O
相切
相离
(4)归纳概括:
如果⊙O的半径为r ,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交 falsed
(3)直线l和⊙O相离 falsed>r.
(5)练一练:
34290004997451.设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:
217170025400d=4,r=3 (2)d=1,r= (3)
5715000(4)
2.在直角三角形ABC 中, ∠ACB=90°,CA=3,CB=4.设⊙C 的半径为r. 请根据r的下列值,判断AB与⊙C 的位置关系,并说明理由.
(1) r=2 (2) r=2.4 (3) r=3
6、切线的判定定理
(1)分析d=r的几何表示,引出切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)证明定理.师生共同分析该定理的条件和结论,画出图形,写出已知、求证,指导学生完成证明.
7、例题讲解
3886200229870O
M
O
M
例1:经过⊙O上一点M作⊙O的切线.
作法:1、联结OM.
2、过点M作直线l垂直于OM.
则直线l就是所求作的切线.
(作图由学生自己完成)
例2:已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(三)巩固练习
1、如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)圆心为点C、半径长R为2的圆与直线AB有怎样的位置关系?
(2)圆心为点C、半径长R为4的圆与直线AB有怎样的位置关系?
(3)如果以点C为圆心的圆与直线AB有公共点,求⊙C的半径R的取值范围.
2、船有无触礁的危险?
海中有一个小岛P,该岛四周12海里内暗礁.今有货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行. 你认为货轮继续向东航行途中会有触礁的危险吗?
(四)课堂小结:
说说这节课的收获和体验,让大家一起分享!
(五)布置作业:习题27.4
