沪教版(上海)数学九年级第二学期-27.4 直线与圆的位置关系 教案
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.4 直线与圆的位置关系 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 62.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览


文档简介
直线与圆的位置关系
教学目标:
1、知道直线和圆相交、相切、相离的定义,根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置关系。
2、学生通过观察、看图、分析、类比,能找出圆心到直线的距离和圆的半径之间的数量关系,揭示直线和圆的关系,并能理解直线与圆相切的判定定理。
3、通过直线和圆的位置关系的探究,对研究过程的反思,渗透分类、数形结合的思想,培养观察、分析和概括的能力.
教学重点与难点
重点是直线和圆的三种位置关系的性质与判定的应用。难点是确定直线和圆的公共点的唯一,以及探索用数量关系来判定直线和圆的位置关系的方法。
教学过程设计
一、通过操作活动,引入新课
操作:请同学在白纸上画一条直线,把一个圆形硬币看作一个圆,将硬币缓缓移动,逐步接近直线,在硬币移动的过程中观察直线与圆的公共点的个数。
2286001342390l
l
l
(1)
(2)
(3)
O
O
O
l
l
l
(1)
(2)
(3)
O
O
O
二、新课讲授
1、观察
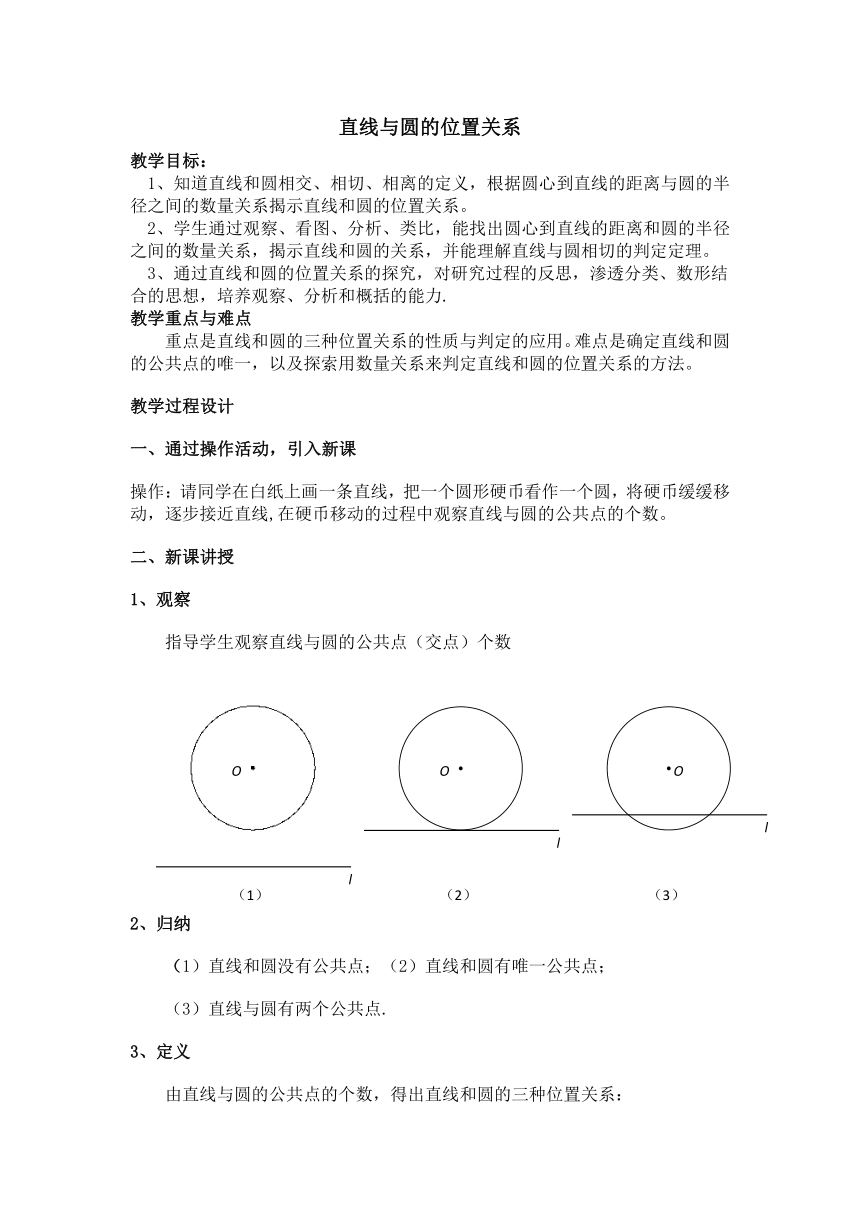
指导学生观察直线与圆的公共点(交点)个数
2、归纳
(1)直线和圆没有公共点;(2)直线和圆有唯一公共点;
(3)直线与圆有两个公共点.
3、定义
由直线与圆的公共点的个数,得出直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线.
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点.
(3)相离:直线和圆没有公共点时,叫做直线和圆相离.
4、理解
提出问题:(1)大家有没有疑问,直线与圆的公共点有可能出现三个或三个以上吗?
若有三个,经过同一直线的三个点能确定一个圆,与不在同一直线上的三点确定一个圆相矛盾。
(同一直线上三个以上的点更加不能确定一个圆),所以直线与圆最多只有两个公共点。
直线与圆有唯一公共点的含义是“有且仅有”,这与直线与圆有一个公共点的含义不同处.
怎样才能正确判断直线和圆的公共点有且只有一个呢?或两个或者没有呢?
5、探索直线与圆的位置关系的数量特征
(1)类比:点与圆的位置关系
(1)点P在⊙O内d (2)点P在⊙O上d=r;
(3)点P在⊙O外d>r
①圆心到直线上一点的距离大于半径能不能判断直线和圆相离?应该怎样判断?(所有的点)但不能操作,不可能每个点都去判断。
②圆心到直线上一点的距离等于半径能不能判断直线与圆相切?(不能)
③圆心到直线上一点的距离小于半径能不能判断直线与圆相交?(能,说明直线上有点在圆内)
④那有没有统一的标准来判断直线与圆的位置关系呢?为什么圆心到直线的距离与半径的大小关系能判断呢?怎样说明直线与圆有一个唯一的公共点?
(2)归纳概括:
如果⊙O的半径为r ,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交 falsed (2)直线l和⊙O相切 falsed=r;
(3)直线l和⊙O相离 falsed>r.
(设计意图:用圆心到点的距离与半径的数量关系判断点与圆的位置关系,而直线与圆的位置关系为什么用圆心到直线的距离和半径的数量关系来判断呢?让学生理解判断方法的合理和必要性。
6、例题讲解引出切线的判定定理
3886200229870O
M
O
M
例1、经过⊙O上一点M作⊙O的切线.
作法:1、联结OM.
2、过点M作直线l垂直于OM.
则直线l就是所求作的切线.
(作图由学生自己完成)
切线的判定定理
(1)分析d=r的几何表示,引出切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)证明定理.师生共同分析该定理的条件和结论,画出图形,写出已知、求证,指导学生完成证明.
(设计意图:通过画图体会到除了用数量关系判断直线和圆的位置关系,还可以用图形直接判断,从而引出判定定理,学生在操作实践中总结出结论)
例2、如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)圆心为点C、半径长R为2的圆与直线AB有怎样的位置关系?
(2)圆心为点C、半径长R为4的圆与直线AB有怎样的位置关系?
(3)如果以点C为圆心的圆与直线AB有公共点,求⊙C的半径R的取值范围.
解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
3747135306070A
B
C
A
B
C
由勾股定理,得AB=5.
设点C到AB的距离为d,则false
即 false
解得 d=2.4.
(1)因为2.4>2,即d>R,
所以,半径长R为2的⊙C与直线AB相离.
(2)因为2.4<4,即d<R,
所以,半径长R为4的⊙C与直线AB相交.
(3)如果以点C为圆心的圆与直线AB有公共点,那么⊙C与直线AB相切或相交.
所以,当R≥2.4时,⊙C与直线AB有公共点.
变式拓展练习:
已知△ABC中,∠C=false,AC=3,BC=4,以C为圆心作⊙C,问:
如果⊙C与斜边AB有且只有一个公共点,那么⊙C的半径长R的取值范围是什么?
如果⊙C与斜边AB有两个公共点,那么⊙C的半径长R的取值范围是什么?
4457700105410A
B
C
A
B
C
如果⊙C与斜边AB没有公共点,那么⊙C的半径R的取值范围是什么?
(设计意图:把直线换为线段,圆与直线的一部分---线段的关系就不一样了,复杂了,一个公共点或没有公共点都有可能圆与直线是相切、或相交)
三、巩固练习
练习27.4 1、2、3.
四、课堂小结
190500158115
教学目标:
1、知道直线和圆相交、相切、相离的定义,根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置关系。
2、学生通过观察、看图、分析、类比,能找出圆心到直线的距离和圆的半径之间的数量关系,揭示直线和圆的关系,并能理解直线与圆相切的判定定理。
3、通过直线和圆的位置关系的探究,对研究过程的反思,渗透分类、数形结合的思想,培养观察、分析和概括的能力.
教学重点与难点
重点是直线和圆的三种位置关系的性质与判定的应用。难点是确定直线和圆的公共点的唯一,以及探索用数量关系来判定直线和圆的位置关系的方法。
教学过程设计
一、通过操作活动,引入新课
操作:请同学在白纸上画一条直线,把一个圆形硬币看作一个圆,将硬币缓缓移动,逐步接近直线,在硬币移动的过程中观察直线与圆的公共点的个数。
2286001342390l
l
l
(1)
(2)
(3)
O
O
O
l
l
l
(1)
(2)
(3)
O
O
O
二、新课讲授
1、观察
指导学生观察直线与圆的公共点(交点)个数
2、归纳
(1)直线和圆没有公共点;(2)直线和圆有唯一公共点;
(3)直线与圆有两个公共点.
3、定义
由直线与圆的公共点的个数,得出直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线.
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切.这时直线叫做圆的切线,唯一的公共点叫做切点.
(3)相离:直线和圆没有公共点时,叫做直线和圆相离.
4、理解
提出问题:(1)大家有没有疑问,直线与圆的公共点有可能出现三个或三个以上吗?
若有三个,经过同一直线的三个点能确定一个圆,与不在同一直线上的三点确定一个圆相矛盾。
(同一直线上三个以上的点更加不能确定一个圆),所以直线与圆最多只有两个公共点。
直线与圆有唯一公共点的含义是“有且仅有”,这与直线与圆有一个公共点的含义不同处.
怎样才能正确判断直线和圆的公共点有且只有一个呢?或两个或者没有呢?
5、探索直线与圆的位置关系的数量特征
(1)类比:点与圆的位置关系
(1)点P在⊙O内d
(3)点P在⊙O外d>r
①圆心到直线上一点的距离大于半径能不能判断直线和圆相离?应该怎样判断?(所有的点)但不能操作,不可能每个点都去判断。
②圆心到直线上一点的距离等于半径能不能判断直线与圆相切?(不能)
③圆心到直线上一点的距离小于半径能不能判断直线与圆相交?(能,说明直线上有点在圆内)
④那有没有统一的标准来判断直线与圆的位置关系呢?为什么圆心到直线的距离与半径的大小关系能判断呢?怎样说明直线与圆有一个唯一的公共点?
(2)归纳概括:
如果⊙O的半径为r ,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交 falsed
(3)直线l和⊙O相离 falsed>r.
(设计意图:用圆心到点的距离与半径的数量关系判断点与圆的位置关系,而直线与圆的位置关系为什么用圆心到直线的距离和半径的数量关系来判断呢?让学生理解判断方法的合理和必要性。
6、例题讲解引出切线的判定定理
3886200229870O
M
O
M
例1、经过⊙O上一点M作⊙O的切线.
作法:1、联结OM.
2、过点M作直线l垂直于OM.
则直线l就是所求作的切线.
(作图由学生自己完成)
切线的判定定理
(1)分析d=r的几何表示,引出切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)证明定理.师生共同分析该定理的条件和结论,画出图形,写出已知、求证,指导学生完成证明.
(设计意图:通过画图体会到除了用数量关系判断直线和圆的位置关系,还可以用图形直接判断,从而引出判定定理,学生在操作实践中总结出结论)
例2、如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)圆心为点C、半径长R为2的圆与直线AB有怎样的位置关系?
(2)圆心为点C、半径长R为4的圆与直线AB有怎样的位置关系?
(3)如果以点C为圆心的圆与直线AB有公共点,求⊙C的半径R的取值范围.
解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
3747135306070A
B
C
A
B
C
由勾股定理,得AB=5.
设点C到AB的距离为d,则false
即 false
解得 d=2.4.
(1)因为2.4>2,即d>R,
所以,半径长R为2的⊙C与直线AB相离.
(2)因为2.4<4,即d<R,
所以,半径长R为4的⊙C与直线AB相交.
(3)如果以点C为圆心的圆与直线AB有公共点,那么⊙C与直线AB相切或相交.
所以,当R≥2.4时,⊙C与直线AB有公共点.
变式拓展练习:
已知△ABC中,∠C=false,AC=3,BC=4,以C为圆心作⊙C,问:
如果⊙C与斜边AB有且只有一个公共点,那么⊙C的半径长R的取值范围是什么?
如果⊙C与斜边AB有两个公共点,那么⊙C的半径长R的取值范围是什么?
4457700105410A
B
C
A
B
C
如果⊙C与斜边AB没有公共点,那么⊙C的半径R的取值范围是什么?
(设计意图:把直线换为线段,圆与直线的一部分---线段的关系就不一样了,复杂了,一个公共点或没有公共点都有可能圆与直线是相切、或相交)
三、巩固练习
练习27.4 1、2、3.
四、课堂小结
190500158115
