沪科版数学九年级下24章 直线和圆的位置关系经典题型汇编(word含答案)
文档属性
| 名称 | 沪科版数学九年级下24章 直线和圆的位置关系经典题型汇编(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 86.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 13:37:23 | ||
图片预览




文档简介
1268730010693400沪科版九年级数学直线和圆的位置关系经典题型汇编
一、 选择题
1.以坐标原点O为圆心,作半径为2的圆.若直线y=-x+b与⊙O相交,则b的取值范围是( )
A. 0≤b<2 B. -2≤b≤2 C. -22.如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
A. 5 B. 6 C. 7 D. 8
3.如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠B的度数为( )
A. 20° B. 25° C. 30° D. 40°
4.如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的度数为( )
A. 29° B. 32° C. 42° D. 58°
5. 如图,直线AD是⊙O的切线,A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A. 54° B. 36° C. 30° D. 27°
6. 如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线垂直于边AD所在的直线于点M.若∠ABC=55°,则∠ACD的度数为( )
A. 20° B. 35° C. 40° D. 55°
7. 如图,⊙O是△ABC的内切圆,则O是△ABC的( )
A. 三条边的垂直平分线的交点 B. 三条角平分线的交点
C. 三条中线的交点 D. 三条高的交点
8.如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的度数为( )
A. 114° B. 122° C. 123° D. 132°
9.已知一个三角形的三边长分别为5,7,8,则其内切圆的半径为( )
A. B. C. D. 2
10. 若正方形的外接圆半径为2,则其内切圆的半径为( )
A. B. 2 C. D. 1
11.如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A. B. C. D.
12.如图,AB是⊙O的直径,PA 切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A. 5 B. 5 C. 5 D.
13.如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径为( )
A. 5 B. 6 C. 2 D. 3
二、 填空题
14.如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________°.
15. (2017·齐齐哈尔)如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠A=50°,则∠COD的度数为________.
16. 如图,AB是⊙O的直径,AC与⊙O相切,切点为A,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°.
17. 如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=________°.
18. 如图,线段AB与⊙O相切于点B,线段AO与⊙O相交于点C,AB=12,AC=8,则⊙O的半径为________.
19.如图,在Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,则弦BE的长为________ .
20.如图,∠AOB=30°,在射线OA上取点O1,以点O1为圆心的圆与OB相切;在射线O1A上取点O2,以点O2为圆心、O2O1为半径的圆与OB相切;在射线O2A上取点O3,以点O3为圆心、O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以点O10为圆心、O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径是________.
21.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于点E,F,连接BD.
(1) AF,EF所在直线的位置关系是________;
(2) 若AC=6,CF=2,则⊙O的半径为________.
22. 如图,⊙C的半径为3,圆外一定点O满足OC=5,P为⊙C上一动点,经过点O的直线l上有两点A,B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为________.
23. 如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=-x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是________.
24.如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是(3,0),(0,2).动点P在直线y=x上运动,以点P为圆心、PB长为半径的⊙P随点P运动.当⊙P与?ABCO的边相切时,点P的坐标为____________________.
三、 解答题
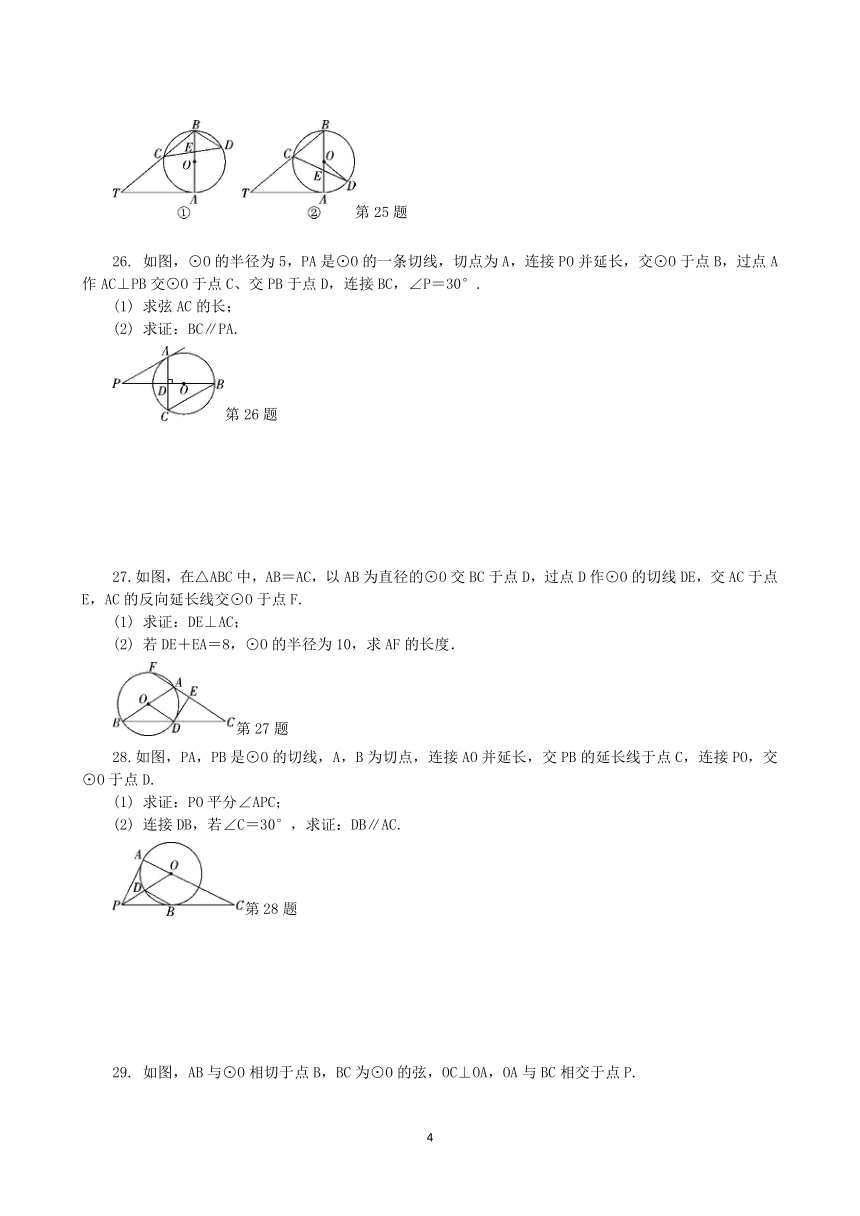
25.已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1) 如图①,求∠T和∠CDB的大小;
(2) 如图②,当BE=BC时,求∠CDO的大小.
26. 如图,⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,∠P=30°.
(1) 求弦AC的长;
(2) 求证:BC∥PA.
27.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1) 求证:DE⊥AC;
(2) 若DE+EA=8,⊙O的半径为10,求AF的长度.
28.如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1) 求证:PO平分∠APC;
(2) 连接DB,若∠C=30°,求证:DB∥AC.
29. 如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1) 求证:AP=AB;
(2) 若OB=4,AB=3,求线段BP的长.
30. 如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1) 求证:∠A=∠ADE;
(2) 若AD=16,DE=10,求BC的长.
31.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1) 判断直线DE与⊙O的位置关系,并说明理由;
(2) 若AC=6,BC=8,OA=2,求线段DE的长.
32.如图,△ABD是⊙O的内接三角形,E是弦BD的中点,C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1) 求证:BC是⊙O的切线;
(2) 若⊙O的半径为6,BC=8,求弦BD的长.
33. 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1) 若点A的坐标为(0,6),点N的坐标为(0,2),∠ABN=30°,求点B的坐标;
(2) 若D为线段NB的中点,求证:直线CD是⊙M的切线.
34如图,在等腰三角形ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB的延长线于点E,垂足为F.
(1) 判断DE与⊙O的位置关系,并说明理由;
(2) 若⊙O的半径R=5,tan C=,求EF的长.
35. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,与AC平行的⊙O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1) 求证:CA=CN;
(2) 连接DF,若cos∠DFA=,AN=2,求⊙O的直径.
36.如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
(1) 求证:AB是⊙O的切线;
(2) 若AC=8,tan∠BAC=,求⊙O的半径.
参考答案
一、 D D B B D A B C C A B A C
二、 50 80° 120 60 5 2 29
(1) AF⊥EF (2) 5 4 2 (0,0)或或
三、 (1) 如图①,连接AC.∵ AT是⊙O的切线,AB是⊙O的直径,∴ AT⊥AB.∴ ∠TAB=90°.∵ ∠ABT=50°,∴ ∠T=90°-∠ABT=40°.∵ AB是⊙O的直径,∴ ∠ACB=90°.∴ ∠CAB=90°-∠ABC=40°.∴ ∠CDB=∠CAB=40° (2) 如图②,连接AD.∵ 在△BCE中,BE=BC,∠EBC=50°,∴ ∠BCE=∠BEC=65°.∴ ∠BAD=∠BCD=65°.∵ OA=OD,∴ ∠ODA=∠OAD=65°.∵ ∠ADC=∠ABC=50°,∴ ∠CDO=∠ODA-∠ADC=65°-50°=15°
(1) 连接OA.∵ PA是⊙O的切线,OA为⊙O的半径,∴ ∠PAO=90°.∵ 在Rt△PAO中,∠P=30°,OA=5,∴ OP=2OA=10,PA==5.∵ AC⊥PB,∴ OP×AD=PA×OA,即×10×AD=×5×5,解得AD=.∵ AC⊥PB,PB过圆心O,∴ AD=DC.∴ AC=2AD=5 (2) ∵ AC⊥PB,∠P=30°,∴ ∠PAC=60°.∵ 在Rt△PAO中,∠P=30°,∴ ∠AOP=60°.∴ ∠BOA=180°-∠AOP=120°.∴ ∠BCA=∠BOA=60°.∴ ∠PAC=∠BCA.∴ BC∥PA
(1) ∵ OB=OD,∴ ∠ABC=∠ODB.∵ AB=AC,∴ ∠ABC=∠ACB.∴ ∠ODB=∠ACB.∴ OD∥AC.∵ DE 是⊙O的切线,OD是半径,∴ DE⊥OD.∴ DE⊥AC (2) 过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,∴ 四边形ODEH是矩形.∴ OD=EH,OH=DE.设AH=x.∵ DE+AE=8,OD=10,∴ AE=10-x,OH=DE=8-(10-x)=x-2.在Rt△AOH中,由勾股定理,知AH2+OH2=OA2,即x2+(x-2)2=102,解得x1=8,x2=-6(不合题意,舍去).∴ AH=8.∵ OH⊥AF,∴ AH=FH=AF.∴ AF=2AH=2×8=16
(1) 连接OB.∵ PA,PB是⊙O的切线,∴ OA⊥AP,OB⊥BP.又∵ OA=OB,∴ PO平分∠APC (2) ∵ OA⊥AP,OB⊥BP,∴ ∠CAP=∠OBP=90°.∵ ∠C=30°,∴ ∠APC=90°-∠C=90°-30°=60°.∵ PO平分∠APC,∴ ∠OPC=∠APC=×60°=30°.∴ ∠POB=90°-∠OPC=90°-30°=60°.又∵ OD=OB,∴ △ODB是等边三角形.∴ ∠OBD=60°.∴ ∠DBP=∠OBP-∠OBD=90°-60°=30°.∴ ∠DBP=∠C.∴ DB∥AC
(1) ∵ OC=OB,∴ ∠OCB=∠OBC.∵ AB是⊙O的切线,∴ OB⊥AB.∴ ∠OBA=90°.∴ ∠ABP+∠OBC=90°.∵ OC⊥AO,∴ ∠AOC=90°.∴ ∠OCB+∠CPO=90°.又∵ ∠APB=∠CPO,∴ ∠APB=∠ABP.∴ AP=AB (2) 过点O作OH⊥BC于点H.∵ 在Rt△OAB中,OB=4,AB=3,∴ OA==5.∵ AP=AB=3,∴ OP=2.∴ 在Rt△POC中,PC==2.∵ OC⊥OA,OH⊥BC,∴ S△COP=PC·OH=OC·OP.∴ OH==.∴ 在Rt△CHO中,CH==.∵ OH⊥BC,OH过圆心O,∴ CH=BH.∴ BC=2CH=.∴ BP=BC-PC=-2=
(1) 如图,连接OD.∵ DE是切线,∴ ∠ODE=90°.∴ ∠ADE+∠BDO=90°.∵ ∠ACB=90°,∴ ∠A+∠B=90°.∵ OD=OB,∴ ∠B=∠BDO.∴ ∠A=∠ADE (2) 如图,连接CD.∵ ∠ADE=∠A,∴ AE=DE.∵ BC是⊙O的直径,∠ACB=90°,∴ EC是⊙O的切线.∴ ED=EC.∴ AE=EC.∵ DE=10,∴ AC=2DE=20.∵ AE=DE=CE,∴ ∠A=∠EDA,∠EDC=∠ECD.∵ ∠A+∠EDA+∠EDC+∠ECD=180°,∴ ∠ADE+∠EDC=×180°=90°.∴ 在Rt△ADC中,DC==12.∵ BC是⊙O的直径,∴ ∠BDC=90°.设BD=x,在 Rt△BDC中,BC2=x2+122;在Rt△ABC中,BC2=(x+16)2-202.∴ x2+122=(x+16)2-202,解得x=9,即BD=9.∴ 在Rt△BDC中,BC==15
(1) 直线DE与⊙O相切 理由:如图,连接OD.∵ OD=OA,∴ ∠A=∠ODA.∵ EF是BD的垂直平分线,∴ EB=ED.∴ ∠B=∠EDB.∵ ∠C=90°,∴ ∠A+∠B=90°.∴ ∠ODA+∠EDB=90°.∴ ∠ODE=180°-90°=90°,即OD⊥DE.∵ OD是⊙O的半径,∴ 直线DE与⊙O相切.
(2) 如图,连接OE.设DE=x,则EB=ED=x,CE=8-x.∵ ∠C=∠ODE=90°,∴ OC2+CE2=OE2=OD2+DE2.∵ AC=6,AO=2,∴ OC=4.∴ 42+(8-x)2=22+x2,解得x=4.75.∴ DE=4.75
(1) 如图,连接OB,OD.∵ E是弦BD的中点,∴ BE=DE,BD=2BE.∵ OB=OD,∴ OE⊥BD,∠BOF=∠DOF,即∠BOD=2∠BOF.∵ ∠BOD=2∠A,∴ ∠BOF=∠A.∵ ∠DBC=∠A,∴ ∠BOF=∠DBC.∵ 在Rt△BEO中,∠DBO+∠BOF=90°,∴ ∠DBO+∠DBC=90°,即∠CBO=90°.∴ CB⊥OB.∵ OB是⊙O的半径,∴ BC是⊙O的切线 (2) ∵ ∠CBO=90°,OB=6,BC=8,∴ OC==10.∵ BE⊥OC,∴ S△OBC=OC·BE=OB·BC.∴ BE===4.8.∴ BD=2BE=9.6
(1) ∵ 点A的坐标为(0,6),点N的坐标为(0,2),∴ ON=2,AN=4.∵ NB∥x轴,x轴⊥y轴,∴ NB⊥y轴.∴ ∠ANB=90°.∵ 在Rt△ANB中,∠ABN=30°,∴ AB=2AN=8.∴ 由勾股定理,可知NB==4.∴ 点B的坐标为(4,2) (2) 如图,连接MC,NC.∵ AN 是⊙M的直径,∴ ∠ACN=90°.∴ ∠NCB=90°.在Rt△NCB中,D为NB的中点,∴ CD=NB=ND.∴ ∠CND=∠NCD.∵ MC=MN,∴ ∠MCN=∠MNC.∵ ∠ANB=∠MNC+∠CND=90°,∴ ∠MCN+∠NCD=90°,即∠MCD=90°.∴ MC⊥CD.∵ MC是⊙M的半径,∴ 直线CD是⊙M的切线
(1) DE与⊙O相切 理由:如图,连接OD.∵ OC=OD,∴ ∠C=∠ODC.∵ AB=BC,∴ ∠C=∠A.∴ ∠ODC=∠A.∴ OD∥AB.∵ DE⊥AB,∴ DE⊥OD.∵ OD是⊙O的半径,∴ DE与⊙O相切. (2) 如图,连接BD,过点D作DH⊥BC于点H.∵ BC 为⊙O的直径,∴ ∠CDB=90°.∴ tan C==.不妨设BD=k,则CD=2k,BC==k.∵ BC=2R=10,∴ k=2,即BD=2,CD=4.∵ 在Rt△CDB中,S△CDB=BC·DH=CD·BD,∴ DH==4.∴ 在Rt△OHD中,OH==3.∵ DE⊥OD,DH⊥BC,∴ ∠ODE=∠OHD=90°.∵ ∠DOH=∠EOD,∴ △DOH∽△EOD.∴ =,即=.∴ OE=.∴ EB=OE-OB=-5=.∵ OD∥AB,即BF∥OD,∴ △BFE∽△ODE.∴ =,即=.∴ BF=2.∴ 在Rt△BFE中,EF==
(1) 如图,连接OF.∵ OF=OA,∴ ∠OAN=∠OFN.∵ ME 与⊙O相切与点F,∴ OF⊥ME,即∠OFN+∠MFN=90°.∵ CD⊥AB,∴ ∠OAN+∠ANH=90°.∴ ∠MFN=∠ANH.又∵ ME∥AC,∴ ∠MFN=∠NAC.∴ ∠ANH=∠NAC.∴ CA=CN (2) ∵ ∠DFA=∠ACH,cos∠DFA=,∴ cos∠ACH=.∵ CD⊥AB,∴ 在Rt△AHC中,设AC=5a,则HC=4a,AH==3a.由(1)知,CA=CN,∴ NH=a.在 Rt△AHN中,利用勾股定理,得AH2+NH2=AN2,即(3a)2+a2=(2)2,解得a=2.∴ AH=6,HC=8.如图,连接OC,在Rt△OHC中,利用勾股定理,得OH2+HC2=OC2.设⊙O的半径为R,则(R-6)2+82=R2,解得R=.∴ 2R=,即⊙O的直径为
(1) 如图,连接OP,OA,OD,设OP交AD于点E.∵ PA=PD,∴ =,∠AOP=∠DOP.∵ OA=OD,∴ OP⊥AD,AE=DE.∴ ∠1+∠OPA=90°.∵ OP=OA,∴ ∠OAP=∠OPA.∴ ∠1+∠OAP=90°.∵ 四边形ABCD为菱形,∴ 易证∠1=∠2.∴ ∠2+∠OAP=90°,即∠OAB=90°.∴ OA⊥AB.∵ OA是⊙O的半径,∴ AB是⊙O的切线 (2) 如图,连接BD,交AC于点F.∵ 四边形ABCD为菱形,∴ DB与AC互相垂直平分.∵ AC=8,tan∠BAC=,∴ AF=4,tan∠DAC==.∴ DF=2.∴ 在Rt△AFD中,AD==2.∴ AE=.∵ ∠1=∠2,∴ 在Rt△PAE中,tan∠1==.∴ PE=.设⊙O的半径为R,则OE=R-,OA=R.在Rt△OAE中,由OA2=OE2+AE2,得R2=(R-)2+()2,解得R=.∴ ⊙O的半径为
一、 选择题
1.以坐标原点O为圆心,作半径为2的圆.若直线y=-x+b与⊙O相交,则b的取值范围是( )
A. 0≤b<2 B. -2≤b≤2 C. -2
A. 5 B. 6 C. 7 D. 8
3.如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠B的度数为( )
A. 20° B. 25° C. 30° D. 40°
4.如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的度数为( )
A. 29° B. 32° C. 42° D. 58°
5. 如图,直线AD是⊙O的切线,A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A. 54° B. 36° C. 30° D. 27°
6. 如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线垂直于边AD所在的直线于点M.若∠ABC=55°,则∠ACD的度数为( )
A. 20° B. 35° C. 40° D. 55°
7. 如图,⊙O是△ABC的内切圆,则O是△ABC的( )
A. 三条边的垂直平分线的交点 B. 三条角平分线的交点
C. 三条中线的交点 D. 三条高的交点
8.如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的度数为( )
A. 114° B. 122° C. 123° D. 132°
9.已知一个三角形的三边长分别为5,7,8,则其内切圆的半径为( )
A. B. C. D. 2
10. 若正方形的外接圆半径为2,则其内切圆的半径为( )
A. B. 2 C. D. 1
11.如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A. B. C. D.
12.如图,AB是⊙O的直径,PA 切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A. 5 B. 5 C. 5 D.
13.如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径为( )
A. 5 B. 6 C. 2 D. 3
二、 填空题
14.如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________°.
15. (2017·齐齐哈尔)如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠A=50°,则∠COD的度数为________.
16. 如图,AB是⊙O的直径,AC与⊙O相切,切点为A,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°.
17. 如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=________°.
18. 如图,线段AB与⊙O相切于点B,线段AO与⊙O相交于点C,AB=12,AC=8,则⊙O的半径为________.
19.如图,在Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,则弦BE的长为________ .
20.如图,∠AOB=30°,在射线OA上取点O1,以点O1为圆心的圆与OB相切;在射线O1A上取点O2,以点O2为圆心、O2O1为半径的圆与OB相切;在射线O2A上取点O3,以点O3为圆心、O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以点O10为圆心、O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径是________.
21.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于点E,F,连接BD.
(1) AF,EF所在直线的位置关系是________;
(2) 若AC=6,CF=2,则⊙O的半径为________.
22. 如图,⊙C的半径为3,圆外一定点O满足OC=5,P为⊙C上一动点,经过点O的直线l上有两点A,B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为________.
23. 如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=-x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是________.
24.如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是(3,0),(0,2).动点P在直线y=x上运动,以点P为圆心、PB长为半径的⊙P随点P运动.当⊙P与?ABCO的边相切时,点P的坐标为____________________.
三、 解答题
25.已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1) 如图①,求∠T和∠CDB的大小;
(2) 如图②,当BE=BC时,求∠CDO的大小.
26. 如图,⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,∠P=30°.
(1) 求弦AC的长;
(2) 求证:BC∥PA.
27.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1) 求证:DE⊥AC;
(2) 若DE+EA=8,⊙O的半径为10,求AF的长度.
28.如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1) 求证:PO平分∠APC;
(2) 连接DB,若∠C=30°,求证:DB∥AC.
29. 如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.
(1) 求证:AP=AB;
(2) 若OB=4,AB=3,求线段BP的长.
30. 如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1) 求证:∠A=∠ADE;
(2) 若AD=16,DE=10,求BC的长.
31.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1) 判断直线DE与⊙O的位置关系,并说明理由;
(2) 若AC=6,BC=8,OA=2,求线段DE的长.
32.如图,△ABD是⊙O的内接三角形,E是弦BD的中点,C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1) 求证:BC是⊙O的切线;
(2) 若⊙O的半径为6,BC=8,求弦BD的长.
33. 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1) 若点A的坐标为(0,6),点N的坐标为(0,2),∠ABN=30°,求点B的坐标;
(2) 若D为线段NB的中点,求证:直线CD是⊙M的切线.
34如图,在等腰三角形ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB的延长线于点E,垂足为F.
(1) 判断DE与⊙O的位置关系,并说明理由;
(2) 若⊙O的半径R=5,tan C=,求EF的长.
35. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,与AC平行的⊙O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1) 求证:CA=CN;
(2) 连接DF,若cos∠DFA=,AN=2,求⊙O的直径.
36.如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
(1) 求证:AB是⊙O的切线;
(2) 若AC=8,tan∠BAC=,求⊙O的半径.
参考答案
一、 D D B B D A B C C A B A C
二、 50 80° 120 60 5 2 29
(1) AF⊥EF (2) 5 4 2 (0,0)或或
三、 (1) 如图①,连接AC.∵ AT是⊙O的切线,AB是⊙O的直径,∴ AT⊥AB.∴ ∠TAB=90°.∵ ∠ABT=50°,∴ ∠T=90°-∠ABT=40°.∵ AB是⊙O的直径,∴ ∠ACB=90°.∴ ∠CAB=90°-∠ABC=40°.∴ ∠CDB=∠CAB=40° (2) 如图②,连接AD.∵ 在△BCE中,BE=BC,∠EBC=50°,∴ ∠BCE=∠BEC=65°.∴ ∠BAD=∠BCD=65°.∵ OA=OD,∴ ∠ODA=∠OAD=65°.∵ ∠ADC=∠ABC=50°,∴ ∠CDO=∠ODA-∠ADC=65°-50°=15°
(1) 连接OA.∵ PA是⊙O的切线,OA为⊙O的半径,∴ ∠PAO=90°.∵ 在Rt△PAO中,∠P=30°,OA=5,∴ OP=2OA=10,PA==5.∵ AC⊥PB,∴ OP×AD=PA×OA,即×10×AD=×5×5,解得AD=.∵ AC⊥PB,PB过圆心O,∴ AD=DC.∴ AC=2AD=5 (2) ∵ AC⊥PB,∠P=30°,∴ ∠PAC=60°.∵ 在Rt△PAO中,∠P=30°,∴ ∠AOP=60°.∴ ∠BOA=180°-∠AOP=120°.∴ ∠BCA=∠BOA=60°.∴ ∠PAC=∠BCA.∴ BC∥PA
(1) ∵ OB=OD,∴ ∠ABC=∠ODB.∵ AB=AC,∴ ∠ABC=∠ACB.∴ ∠ODB=∠ACB.∴ OD∥AC.∵ DE 是⊙O的切线,OD是半径,∴ DE⊥OD.∴ DE⊥AC (2) 过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,∴ 四边形ODEH是矩形.∴ OD=EH,OH=DE.设AH=x.∵ DE+AE=8,OD=10,∴ AE=10-x,OH=DE=8-(10-x)=x-2.在Rt△AOH中,由勾股定理,知AH2+OH2=OA2,即x2+(x-2)2=102,解得x1=8,x2=-6(不合题意,舍去).∴ AH=8.∵ OH⊥AF,∴ AH=FH=AF.∴ AF=2AH=2×8=16
(1) 连接OB.∵ PA,PB是⊙O的切线,∴ OA⊥AP,OB⊥BP.又∵ OA=OB,∴ PO平分∠APC (2) ∵ OA⊥AP,OB⊥BP,∴ ∠CAP=∠OBP=90°.∵ ∠C=30°,∴ ∠APC=90°-∠C=90°-30°=60°.∵ PO平分∠APC,∴ ∠OPC=∠APC=×60°=30°.∴ ∠POB=90°-∠OPC=90°-30°=60°.又∵ OD=OB,∴ △ODB是等边三角形.∴ ∠OBD=60°.∴ ∠DBP=∠OBP-∠OBD=90°-60°=30°.∴ ∠DBP=∠C.∴ DB∥AC
(1) ∵ OC=OB,∴ ∠OCB=∠OBC.∵ AB是⊙O的切线,∴ OB⊥AB.∴ ∠OBA=90°.∴ ∠ABP+∠OBC=90°.∵ OC⊥AO,∴ ∠AOC=90°.∴ ∠OCB+∠CPO=90°.又∵ ∠APB=∠CPO,∴ ∠APB=∠ABP.∴ AP=AB (2) 过点O作OH⊥BC于点H.∵ 在Rt△OAB中,OB=4,AB=3,∴ OA==5.∵ AP=AB=3,∴ OP=2.∴ 在Rt△POC中,PC==2.∵ OC⊥OA,OH⊥BC,∴ S△COP=PC·OH=OC·OP.∴ OH==.∴ 在Rt△CHO中,CH==.∵ OH⊥BC,OH过圆心O,∴ CH=BH.∴ BC=2CH=.∴ BP=BC-PC=-2=
(1) 如图,连接OD.∵ DE是切线,∴ ∠ODE=90°.∴ ∠ADE+∠BDO=90°.∵ ∠ACB=90°,∴ ∠A+∠B=90°.∵ OD=OB,∴ ∠B=∠BDO.∴ ∠A=∠ADE (2) 如图,连接CD.∵ ∠ADE=∠A,∴ AE=DE.∵ BC是⊙O的直径,∠ACB=90°,∴ EC是⊙O的切线.∴ ED=EC.∴ AE=EC.∵ DE=10,∴ AC=2DE=20.∵ AE=DE=CE,∴ ∠A=∠EDA,∠EDC=∠ECD.∵ ∠A+∠EDA+∠EDC+∠ECD=180°,∴ ∠ADE+∠EDC=×180°=90°.∴ 在Rt△ADC中,DC==12.∵ BC是⊙O的直径,∴ ∠BDC=90°.设BD=x,在 Rt△BDC中,BC2=x2+122;在Rt△ABC中,BC2=(x+16)2-202.∴ x2+122=(x+16)2-202,解得x=9,即BD=9.∴ 在Rt△BDC中,BC==15
(1) 直线DE与⊙O相切 理由:如图,连接OD.∵ OD=OA,∴ ∠A=∠ODA.∵ EF是BD的垂直平分线,∴ EB=ED.∴ ∠B=∠EDB.∵ ∠C=90°,∴ ∠A+∠B=90°.∴ ∠ODA+∠EDB=90°.∴ ∠ODE=180°-90°=90°,即OD⊥DE.∵ OD是⊙O的半径,∴ 直线DE与⊙O相切.
(2) 如图,连接OE.设DE=x,则EB=ED=x,CE=8-x.∵ ∠C=∠ODE=90°,∴ OC2+CE2=OE2=OD2+DE2.∵ AC=6,AO=2,∴ OC=4.∴ 42+(8-x)2=22+x2,解得x=4.75.∴ DE=4.75
(1) 如图,连接OB,OD.∵ E是弦BD的中点,∴ BE=DE,BD=2BE.∵ OB=OD,∴ OE⊥BD,∠BOF=∠DOF,即∠BOD=2∠BOF.∵ ∠BOD=2∠A,∴ ∠BOF=∠A.∵ ∠DBC=∠A,∴ ∠BOF=∠DBC.∵ 在Rt△BEO中,∠DBO+∠BOF=90°,∴ ∠DBO+∠DBC=90°,即∠CBO=90°.∴ CB⊥OB.∵ OB是⊙O的半径,∴ BC是⊙O的切线 (2) ∵ ∠CBO=90°,OB=6,BC=8,∴ OC==10.∵ BE⊥OC,∴ S△OBC=OC·BE=OB·BC.∴ BE===4.8.∴ BD=2BE=9.6
(1) ∵ 点A的坐标为(0,6),点N的坐标为(0,2),∴ ON=2,AN=4.∵ NB∥x轴,x轴⊥y轴,∴ NB⊥y轴.∴ ∠ANB=90°.∵ 在Rt△ANB中,∠ABN=30°,∴ AB=2AN=8.∴ 由勾股定理,可知NB==4.∴ 点B的坐标为(4,2) (2) 如图,连接MC,NC.∵ AN 是⊙M的直径,∴ ∠ACN=90°.∴ ∠NCB=90°.在Rt△NCB中,D为NB的中点,∴ CD=NB=ND.∴ ∠CND=∠NCD.∵ MC=MN,∴ ∠MCN=∠MNC.∵ ∠ANB=∠MNC+∠CND=90°,∴ ∠MCN+∠NCD=90°,即∠MCD=90°.∴ MC⊥CD.∵ MC是⊙M的半径,∴ 直线CD是⊙M的切线
(1) DE与⊙O相切 理由:如图,连接OD.∵ OC=OD,∴ ∠C=∠ODC.∵ AB=BC,∴ ∠C=∠A.∴ ∠ODC=∠A.∴ OD∥AB.∵ DE⊥AB,∴ DE⊥OD.∵ OD是⊙O的半径,∴ DE与⊙O相切. (2) 如图,连接BD,过点D作DH⊥BC于点H.∵ BC 为⊙O的直径,∴ ∠CDB=90°.∴ tan C==.不妨设BD=k,则CD=2k,BC==k.∵ BC=2R=10,∴ k=2,即BD=2,CD=4.∵ 在Rt△CDB中,S△CDB=BC·DH=CD·BD,∴ DH==4.∴ 在Rt△OHD中,OH==3.∵ DE⊥OD,DH⊥BC,∴ ∠ODE=∠OHD=90°.∵ ∠DOH=∠EOD,∴ △DOH∽△EOD.∴ =,即=.∴ OE=.∴ EB=OE-OB=-5=.∵ OD∥AB,即BF∥OD,∴ △BFE∽△ODE.∴ =,即=.∴ BF=2.∴ 在Rt△BFE中,EF==
(1) 如图,连接OF.∵ OF=OA,∴ ∠OAN=∠OFN.∵ ME 与⊙O相切与点F,∴ OF⊥ME,即∠OFN+∠MFN=90°.∵ CD⊥AB,∴ ∠OAN+∠ANH=90°.∴ ∠MFN=∠ANH.又∵ ME∥AC,∴ ∠MFN=∠NAC.∴ ∠ANH=∠NAC.∴ CA=CN (2) ∵ ∠DFA=∠ACH,cos∠DFA=,∴ cos∠ACH=.∵ CD⊥AB,∴ 在Rt△AHC中,设AC=5a,则HC=4a,AH==3a.由(1)知,CA=CN,∴ NH=a.在 Rt△AHN中,利用勾股定理,得AH2+NH2=AN2,即(3a)2+a2=(2)2,解得a=2.∴ AH=6,HC=8.如图,连接OC,在Rt△OHC中,利用勾股定理,得OH2+HC2=OC2.设⊙O的半径为R,则(R-6)2+82=R2,解得R=.∴ 2R=,即⊙O的直径为
(1) 如图,连接OP,OA,OD,设OP交AD于点E.∵ PA=PD,∴ =,∠AOP=∠DOP.∵ OA=OD,∴ OP⊥AD,AE=DE.∴ ∠1+∠OPA=90°.∵ OP=OA,∴ ∠OAP=∠OPA.∴ ∠1+∠OAP=90°.∵ 四边形ABCD为菱形,∴ 易证∠1=∠2.∴ ∠2+∠OAP=90°,即∠OAB=90°.∴ OA⊥AB.∵ OA是⊙O的半径,∴ AB是⊙O的切线 (2) 如图,连接BD,交AC于点F.∵ 四边形ABCD为菱形,∴ DB与AC互相垂直平分.∵ AC=8,tan∠BAC=,∴ AF=4,tan∠DAC==.∴ DF=2.∴ 在Rt△AFD中,AD==2.∴ AE=.∵ ∠1=∠2,∴ 在Rt△PAE中,tan∠1==.∴ PE=.设⊙O的半径为R,则OE=R-,OA=R.在Rt△OAE中,由OA2=OE2+AE2,得R2=(R-)2+()2,解得R=.∴ ⊙O的半径为
