华东师大版八年级数学下册单元测试题 :第19章 矩形、菱形与正方形(Word版 含答案)
文档属性
| 名称 | 华东师大版八年级数学下册单元测试题 :第19章 矩形、菱形与正方形(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:19:06 | ||
图片预览



文档简介
第19章 矩形、菱形与正方形
一、选择题(本大题共10个小题,每小题3分,共30分)
1.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分 C.对角线平分一组对角 D.对角线互相垂直
2.如图,四边形ABCD是平行四边形,连接AC,BD.下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当 AC⊥BD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
第2题图 第3题图 第4题图
3.如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
4.如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A,C重合)且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是( )
A.52 B.2 C.3 D.53
5.在探索“尺规三等分角”这个数学名题的过程中,曾利用了下图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是( )
A.7° B.21° C.23° D.24°
第5题图 第6题图 第7题图
6.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
7.如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A.2 B.22 C.3 D.32
8.如图,在矩形ABCD中,AD=3AB,点G,H分别在AD,BC上,连接BG,DH,且BG∥DH.若四边形BHDG为菱形,则AGAD=( )
A.45 B.35 C.49 D.38
第8题图 第9题图 第10题图
9.如图,在平面直角坐标系xOy中,直线y=-2x+4与x 轴、y轴分别相交于点A,B,四边形ABCD是正方形,双曲线y=kx(k≠0)第一象限的部分经过点D,若使得点C的对应点恰好落在双曲线上,则需将正方形ABCD沿x轴向左平移( )
A.8个单位 B.6个单位 C.4个单位 D.2个单位
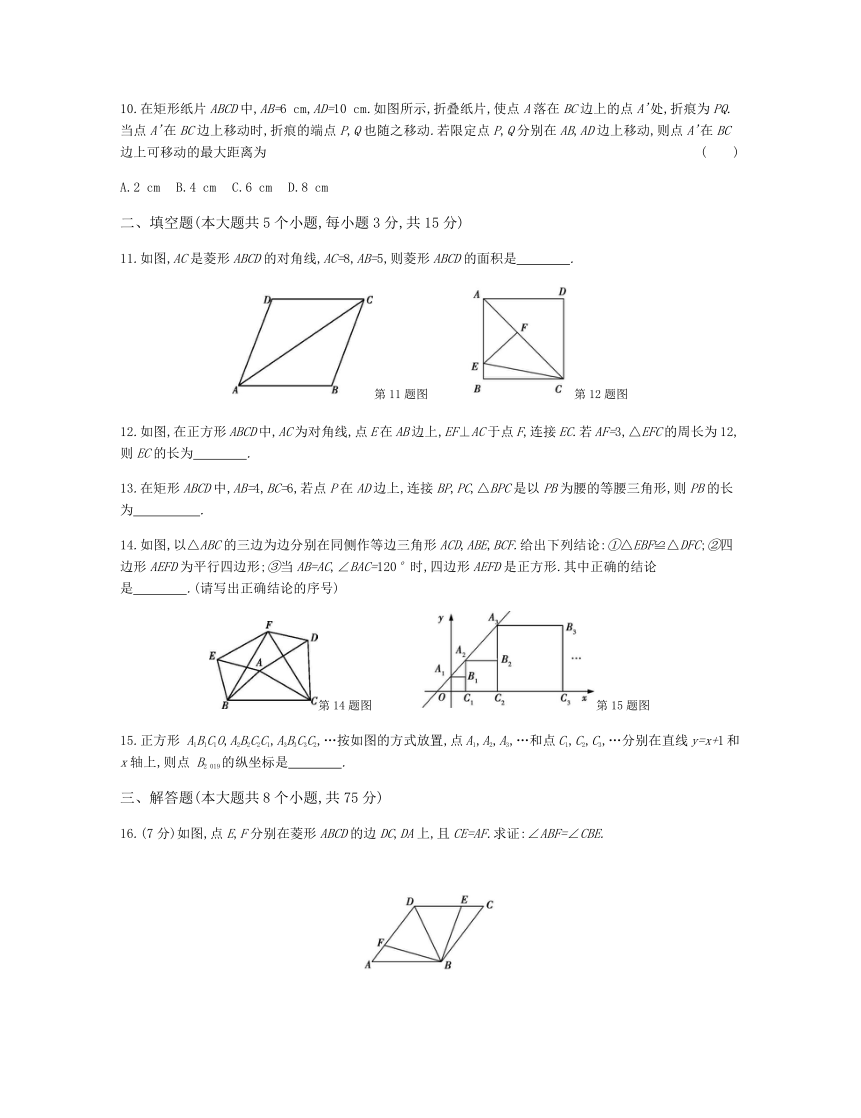
10.在矩形纸片ABCD中,AB=6 cm,AD=10 cm.如图所示,折叠纸片,使点A落在BC边上的点A'处,折痕为PQ.当点A'在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A'在BC边上可移动的最大距离为( )
A.2 cm B.4 cm C.6 cm D.8 cm
二、填空题(本大题共5个小题,每小题3分,共15分)
11.如图,AC是菱形ABCD的对角线,AC=8,AB=5,则菱形ABCD的面积是 .?
第11题图 第12题图
12.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC.若AF=3,△EFC的周长为12,则EC的长为 .?
13.在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP,PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .?
14.如图,以△ABC的三边为边分别在同侧作等边三角形ACD,ABE,BCF.给出下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 .(请写出正确结论的序号)?
第14题图 第15题图
15.正方形 A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点 B2 019的纵坐标是 .?
三、解答题(本大题共8个小题,共75分)
16.(7分)如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.求证:∠ABF=∠CBE.
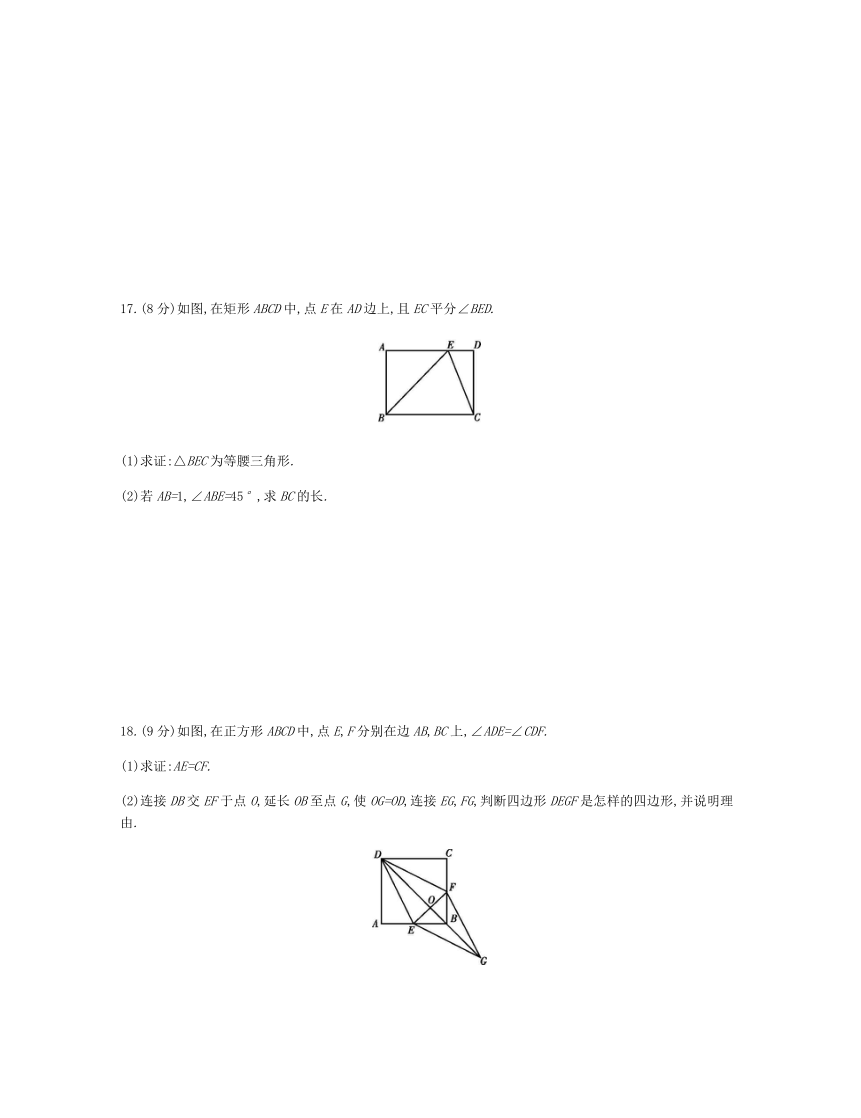
17.(8分)如图,在矩形ABCD中,点E在AD边上,且EC平分∠BED.
(1)求证:△BEC为等腰三角形.
(2)若AB=1,∠ABE=45°,求BC的长.
18.(9分)如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF.
(2)连接DB交EF于点O,延长OB至点G,使OG=OD,连接EG,FG,判断四边形DEGF是怎样的四边形,并说明理由.
19.(9分)如图,将?ABCD的边DA延长到点F,使DA=AF,CF交边AB于点E.
(1)求证:BE=AE.
(2)若2∠D=∠BEF,求证:四边形ACBF是矩形.
20.(10分)如图,正方形ABCD的边长为8 cm,E,F,G,H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形.
(2)判断直线EG是否经过某一定点,并说明理由.
21.(10分)如图,将?ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF.
(2)连接BD,CE.若∠BFD=2∠A,求证:四边形BECD是矩形.
22.(10分)(1)如图1,矩形ABCD的对角线AC,BD相交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.
(2)如果题目中的矩形变为菱形,如图2,结论应变为什么?说明理由.
(3)如果题目中的矩形变为正方形,如图3,结论又应变为什么?说明理由.
23.(12分) 如图1,在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 .?
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,(1)中的结论是否仍然成立?请作出判断并给予说明.
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,(1)中的结论都能成立吗?请作出判断,并给予说明.
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
A
C
C
B
C
D
B
11.24 12.5 13.5或6 14.①② 15.22 018
16. ∵四边形ABCD是菱形,
∴∠A=∠C,AB=BC.
又∵AF=CE,
∴△ABF≌△CBE,
∴∠ABF=∠CBE.
17. (1)∵四边形ABCD是矩形,
∴AD∥BC,∴∠DEC=∠BCE.
∵EC平分∠DEB,∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC,∴△BEC是等腰三角形.
(2)∵四边形ABCD是矩形,∴∠A=90°.
∵∠ABE=45°,
∴∠AEB=∠ABE=45°,
∴AB=AE=1.
在Rt△ABE中,由勾股定理得,BE=12+12=2,
∴BC=BE=2.
18. (1)∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°.
在△DAE和△DCF中,∠ADE=∠CDF,DA=DC,∠A=∠C,
∴△DAE≌△DCF,∴AE=CF.
(2)四边形DEGF是菱形.理由如下:
由(1)知△DAE≌△DCF,∴DE=DF.
∵AE=CF,∴BE=BF,
∴DG是EF的垂直平分线,∴GE=GF.
∵OG=OD,DG⊥EF,∴ED=EG,
∴DE=EG=GF=FD,
∴四边形DEGF是菱形.
19. (1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵DA=AF,∴AF=BC,
∴四边形ACBF是平行四边形,
∴BE=AE.
(2)∵四边形ABCD是平行四边形,∴∠D=∠ABC.
∵2∠D=∠BEF,∠BEF=∠ABC+∠ECB,
∴2∠ABC=∠ABC+∠ECB,
∴∠ECB=∠ABC, ∴CE=BE.
∵四边形ACBF是平行四边形,
∴AE=BE,CE=EF,
∴AB=CF,∴平行四边形ACBF是矩形.
20. (1)∵四边形ABCD是正方形,
∴∠A=∠B=90°,AB=DA.
又∵AE=DH,∴BE= AH.
∵AH=BE,∠A=∠B,AE=BF,
∴△AEH≌△BFE,
∴EH=FE,∠AHE=∠BEF.
同理可得FE=GF=HG,∴EH= FE=GF=HG,
∴四边形EFGH是菱形.
∵∠A=90°,∴∠AHE+∠AEH=90°,
又∵∠AHE=∠BEF,
∴∠BEF+∠AEH=90°,
∴∠FEH=90°,∴四边形EFGH是正方形.
(2)直线EG经过正方形ABCD的中心.理由如下:
如图,连接BD,EG相交于点O.
∵四边形ABCD是正方形,
∴AB∥DC,AB=DC,
∴∠EBD=∠GDB.
∵AE=CG,AB=DC,∴BE=DG.
∵∠EOB=∠GOD,∠EBO=∠GDO,BE=DG,
∴△EOB≌△GOD,
∴BO=DO,即点O为BD的中点,
∴直线EG经过正方形ABCD的中心.
21. (1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∵BE=AB,∴BE=CD.
∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,
在△BEF与△CDF中,∠BEF=∠CDF,BE=CD,∠EBF=∠DCF,
∴△BEF≌△CDF.
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠A=∠DCB.
∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,
∴BF=CF,EF=DF.
∵∠BFD=2∠A,
∴∠BFD=2∠DCF,∴∠DCF=∠FDC,
∴DF=CF,∴DE=BC,
∴四边形BECD是矩形.
22. (1)四边形CODP是菱形.理由如下:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=12AC,OB=OD=12BD,∴OC=OD.
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形.
又∵OC=OD,∴四边形CODP是菱形.
(2)四边形CODP是矩形.理由如下:
∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°.
∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.
又∵∠DOC=90°,∴四边形CODP是矩形.
(3)四边形CODP是正方形.理由如下:
∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=12AC,OB=OD=12BD,
∴∠DOC=90°,OD=OC.
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形.
又∵∠DOC=90°,OD=OC,
∴四边形CODP是正方形.
23. (1)相等 互相垂直
(2)(1)中的结论仍然成立.理由如下:
设AF与BE交于点M.
∵四边形ABCD是正方形,
∴AB=AD=DC.
在△ADE和△DCF中,
∵AE=DF,ED=FC,AD=DC,
∴△ADE≌△DCF,∴∠DAE=∠CDF.
∵四边形ABCD是正方形,∴∠BAD=∠ADC=90°,
∴∠BAE=∠ADF.
在△ABE和△DAF中,AB=DA,∠BAE=∠ADF,AE=DF,∴△ABE≌△DAF,∴BE=AF,∠ABE=∠DAF.
又∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.
∴在△ABM中,∠AMB=180°-(∠ABM+∠BAM)=90°,
∴BE⊥AF.
(3)(1)中的结论都能成立.理由如下:
设AF与BE交于点M'.
∵四边形ABCD是正方形,∴AB=AD=DC.
在△ADE和△DCF中,
AE=DF,ED=FC,AD=DC,
∴△ADE≌△DCF,∴∠DAE=∠CDF.
∵四边形ABCD是正方形,
∴∠BAD=∠ADC=90°,∴∠BAE=∠ADF.
在△ABE和△DAF中,∵AB=DA,∠BAE=∠ADF,AE=DF,
∴△ABE≌△DAF,∴BE=AF,∠ABM'=∠DAF.
又∵∠DAF+∠BAM'=90°,∴∠ABM'+∠BAM'=90°,
∴在△ABM'中,∠AM'B=180°-(∠ABM'+∠BAM')=90°,
∴BE⊥AF.
一、选择题(本大题共10个小题,每小题3分,共30分)
1.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分 C.对角线平分一组对角 D.对角线互相垂直
2.如图,四边形ABCD是平行四边形,连接AC,BD.下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当 AC⊥BD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
第2题图 第3题图 第4题图
3.如图,在?ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )
A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
4.如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A,C重合)且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是( )
A.52 B.2 C.3 D.53
5.在探索“尺规三等分角”这个数学名题的过程中,曾利用了下图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是( )
A.7° B.21° C.23° D.24°
第5题图 第6题图 第7题图
6.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
7.如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A.2 B.22 C.3 D.32
8.如图,在矩形ABCD中,AD=3AB,点G,H分别在AD,BC上,连接BG,DH,且BG∥DH.若四边形BHDG为菱形,则AGAD=( )
A.45 B.35 C.49 D.38
第8题图 第9题图 第10题图
9.如图,在平面直角坐标系xOy中,直线y=-2x+4与x 轴、y轴分别相交于点A,B,四边形ABCD是正方形,双曲线y=kx(k≠0)第一象限的部分经过点D,若使得点C的对应点恰好落在双曲线上,则需将正方形ABCD沿x轴向左平移( )
A.8个单位 B.6个单位 C.4个单位 D.2个单位
10.在矩形纸片ABCD中,AB=6 cm,AD=10 cm.如图所示,折叠纸片,使点A落在BC边上的点A'处,折痕为PQ.当点A'在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A'在BC边上可移动的最大距离为( )
A.2 cm B.4 cm C.6 cm D.8 cm
二、填空题(本大题共5个小题,每小题3分,共15分)
11.如图,AC是菱形ABCD的对角线,AC=8,AB=5,则菱形ABCD的面积是 .?
第11题图 第12题图
12.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC.若AF=3,△EFC的周长为12,则EC的长为 .?
13.在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP,PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .?
14.如图,以△ABC的三边为边分别在同侧作等边三角形ACD,ABE,BCF.给出下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 .(请写出正确结论的序号)?
第14题图 第15题图
15.正方形 A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点 B2 019的纵坐标是 .?
三、解答题(本大题共8个小题,共75分)
16.(7分)如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.求证:∠ABF=∠CBE.
17.(8分)如图,在矩形ABCD中,点E在AD边上,且EC平分∠BED.
(1)求证:△BEC为等腰三角形.
(2)若AB=1,∠ABE=45°,求BC的长.
18.(9分)如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF.
(2)连接DB交EF于点O,延长OB至点G,使OG=OD,连接EG,FG,判断四边形DEGF是怎样的四边形,并说明理由.
19.(9分)如图,将?ABCD的边DA延长到点F,使DA=AF,CF交边AB于点E.
(1)求证:BE=AE.
(2)若2∠D=∠BEF,求证:四边形ACBF是矩形.
20.(10分)如图,正方形ABCD的边长为8 cm,E,F,G,H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形.
(2)判断直线EG是否经过某一定点,并说明理由.
21.(10分)如图,将?ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF.
(2)连接BD,CE.若∠BFD=2∠A,求证:四边形BECD是矩形.
22.(10分)(1)如图1,矩形ABCD的对角线AC,BD相交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.
(2)如果题目中的矩形变为菱形,如图2,结论应变为什么?说明理由.
(3)如果题目中的矩形变为正方形,如图3,结论又应变为什么?说明理由.
23.(12分) 如图1,在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 .?
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,(1)中的结论是否仍然成立?请作出判断并给予说明.
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,(1)中的结论都能成立吗?请作出判断,并给予说明.
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
A
C
C
B
C
D
B
11.24 12.5 13.5或6 14.①② 15.22 018
16. ∵四边形ABCD是菱形,
∴∠A=∠C,AB=BC.
又∵AF=CE,
∴△ABF≌△CBE,
∴∠ABF=∠CBE.
17. (1)∵四边形ABCD是矩形,
∴AD∥BC,∴∠DEC=∠BCE.
∵EC平分∠DEB,∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC,∴△BEC是等腰三角形.
(2)∵四边形ABCD是矩形,∴∠A=90°.
∵∠ABE=45°,
∴∠AEB=∠ABE=45°,
∴AB=AE=1.
在Rt△ABE中,由勾股定理得,BE=12+12=2,
∴BC=BE=2.
18. (1)∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°.
在△DAE和△DCF中,∠ADE=∠CDF,DA=DC,∠A=∠C,
∴△DAE≌△DCF,∴AE=CF.
(2)四边形DEGF是菱形.理由如下:
由(1)知△DAE≌△DCF,∴DE=DF.
∵AE=CF,∴BE=BF,
∴DG是EF的垂直平分线,∴GE=GF.
∵OG=OD,DG⊥EF,∴ED=EG,
∴DE=EG=GF=FD,
∴四边形DEGF是菱形.
19. (1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵DA=AF,∴AF=BC,
∴四边形ACBF是平行四边形,
∴BE=AE.
(2)∵四边形ABCD是平行四边形,∴∠D=∠ABC.
∵2∠D=∠BEF,∠BEF=∠ABC+∠ECB,
∴2∠ABC=∠ABC+∠ECB,
∴∠ECB=∠ABC, ∴CE=BE.
∵四边形ACBF是平行四边形,
∴AE=BE,CE=EF,
∴AB=CF,∴平行四边形ACBF是矩形.
20. (1)∵四边形ABCD是正方形,
∴∠A=∠B=90°,AB=DA.
又∵AE=DH,∴BE= AH.
∵AH=BE,∠A=∠B,AE=BF,
∴△AEH≌△BFE,
∴EH=FE,∠AHE=∠BEF.
同理可得FE=GF=HG,∴EH= FE=GF=HG,
∴四边形EFGH是菱形.
∵∠A=90°,∴∠AHE+∠AEH=90°,
又∵∠AHE=∠BEF,
∴∠BEF+∠AEH=90°,
∴∠FEH=90°,∴四边形EFGH是正方形.
(2)直线EG经过正方形ABCD的中心.理由如下:
如图,连接BD,EG相交于点O.
∵四边形ABCD是正方形,
∴AB∥DC,AB=DC,
∴∠EBD=∠GDB.
∵AE=CG,AB=DC,∴BE=DG.
∵∠EOB=∠GOD,∠EBO=∠GDO,BE=DG,
∴△EOB≌△GOD,
∴BO=DO,即点O为BD的中点,
∴直线EG经过正方形ABCD的中心.
21. (1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.
∵BE=AB,∴BE=CD.
∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,
在△BEF与△CDF中,∠BEF=∠CDF,BE=CD,∠EBF=∠DCF,
∴△BEF≌△CDF.
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠A=∠DCB.
∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,
∴BF=CF,EF=DF.
∵∠BFD=2∠A,
∴∠BFD=2∠DCF,∴∠DCF=∠FDC,
∴DF=CF,∴DE=BC,
∴四边形BECD是矩形.
22. (1)四边形CODP是菱形.理由如下:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=12AC,OB=OD=12BD,∴OC=OD.
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形.
又∵OC=OD,∴四边形CODP是菱形.
(2)四边形CODP是矩形.理由如下:
∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°.
∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.
又∵∠DOC=90°,∴四边形CODP是矩形.
(3)四边形CODP是正方形.理由如下:
∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=12AC,OB=OD=12BD,
∴∠DOC=90°,OD=OC.
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形.
又∵∠DOC=90°,OD=OC,
∴四边形CODP是正方形.
23. (1)相等 互相垂直
(2)(1)中的结论仍然成立.理由如下:
设AF与BE交于点M.
∵四边形ABCD是正方形,
∴AB=AD=DC.
在△ADE和△DCF中,
∵AE=DF,ED=FC,AD=DC,
∴△ADE≌△DCF,∴∠DAE=∠CDF.
∵四边形ABCD是正方形,∴∠BAD=∠ADC=90°,
∴∠BAE=∠ADF.
在△ABE和△DAF中,AB=DA,∠BAE=∠ADF,AE=DF,∴△ABE≌△DAF,∴BE=AF,∠ABE=∠DAF.
又∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.
∴在△ABM中,∠AMB=180°-(∠ABM+∠BAM)=90°,
∴BE⊥AF.
(3)(1)中的结论都能成立.理由如下:
设AF与BE交于点M'.
∵四边形ABCD是正方形,∴AB=AD=DC.
在△ADE和△DCF中,
AE=DF,ED=FC,AD=DC,
∴△ADE≌△DCF,∴∠DAE=∠CDF.
∵四边形ABCD是正方形,
∴∠BAD=∠ADC=90°,∴∠BAE=∠ADF.
在△ABE和△DAF中,∵AB=DA,∠BAE=∠ADF,AE=DF,
∴△ABE≌△DAF,∴BE=AF,∠ABM'=∠DAF.
又∵∠DAF+∠BAM'=90°,∴∠ABM'+∠BAM'=90°,
∴在△ABM'中,∠AM'B=180°-(∠ABM'+∠BAM')=90°,
∴BE⊥AF.
