华东师大版八年级数学下册单元测试题: 第20章 数据的整理与初步处理(Word版 含答案)
文档属性
| 名称 | 华东师大版八年级数学下册单元测试题: 第20章 数据的整理与初步处理(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 634.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:19:50 | ||
图片预览




文档简介
第20章 数据的整理与初步处理
一、选择题(本大题共10个小题,每题3分,共30分)
1.某同学参加数学、物理、化学三科竞赛,平均成绩是93分,其中数学97分,化学89分,那么物理成绩是( )
A.91分 B.92分 C.93分 D.94分
2.统计学校排球队员的年龄,结果如下表:
年龄(岁)
12
13
14
15
人数
2
4
6
8
根据表中信息可以判断该学校排球队员的平均年龄为( )
A.13岁 B.14岁 C.13.5岁 D.15岁
3.下列说法错误的是( )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
4.对于一组统计数据3,3,6,5,3,下列说法错误的是( )
A.众数是3 B.平均数是4 C.方差是1.6 D.中位数是6
5.为落实中央扶贫攻坚工作,实施精准扶贫方略,广泛动员全社会力量参与扶贫,校团委开展爱心捐款活动,将某班50名学生捐款情况绘制成了统计图(如图),根据图中提供的信息,此次捐款的众数和中位数分别是( )
A.20元、20元 B.30元、20元 C. 30元、30元 D.20元、30元
第5题图 第6题图
6.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调查结果绘制成如图所示的条形统计图和扇形统计图.根据图中信息,这些学生成绩的平均数和中位数分别是( )
A.2.95分、10分 B.2.5分、2分 C.2.95分、3分 D.3分、4分
7.如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( )
A.甲的数学成绩高于班级平均分,且成绩比较稳定
B.乙的数学成绩在班级平均分附近波动,且比丙好
C.丙的数学成绩低于班级平均分,但成绩逐次提高
D.就甲、乙、丙三个人而言,乙的数学成绩最不稳定
8.某校合唱团有30名成员,合唱团成员的年龄分布统计表如下:
年龄(岁)
13
14
15
16
频数
5
15
x
10-x
则对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数 B.平均数、方差 C.众数、中位数 D.众数、方差
9.在某次考试中,甲、乙、丙、丁四位同学的数学成绩(百分制)分别为85分,90分,x分,80分,若这组数据的众数与平均数相等,则这组数据的中位数是( )
A.85 B.90 C.80 D.70
10.甲、乙两班举行电脑汉字输入比赛,参赛学生人数及每分钟输入汉字的个数经统计计算后的结果如下表:
班级
参加人数
中位数(个)
方差
平均数(个)
甲
55
149
191
135
乙
55
151
110
135
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀(每分钟输入汉字个数大于等于150为优秀)的人数多于甲班优秀的人数;③甲班成绩的波动比乙班成绩的波动小.
上述结论中正确的是( )
A.①②③ B.①② C.①③ D.②③
二、填空题(本大题共5个小题,每题3分,共15分)
11.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
一周在校的体育锻炼时间(h)
5
6
7
8
人数
2
5
6
2
那么这15名学生这一周在校的体育锻炼时间的众数是 h.?
12.在学校的卫生检查中,规定各班的教室桌面和黑板卫生成绩占30%,地面卫生成绩占40%,个人卫生成绩占30%.八年级(1)班这三项成绩分别为85分,90分和95分,则该班卫生检查的总成绩为 .?
13.已知一组数据x1,x2,x3的平均数是5,方差是2,那么另一组数据2x1-4,2x2-4,2x3-4的平均数和方差分别是 .?
14.若3,a,4,5的众数是4,则这组数据的平均数是 .?
15.已知20个数据的平均数为6,且这20个数据的平方和为800,则这组数据的方差等于 .?
三、解答题(本大题共8个小题,共75分)
16.(8分)为了宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数.
17.(8分)某厂为了检验甲、乙两车间生产的同一种零件的直径(单位:mm)的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:
170~174
175~179
180~184
185~189
甲车间
1
3
4
2
乙车间
0
6
2
2
(1)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(2)若该零件的直径在175~184 mm的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
18.(8分)某单位招聘员工,采取笔试与面试相结合的方式,两项成绩的原始分均为100分.前6名选手的得分如下:
项目序号
1
2
3
4
5
6
笔试成绩(分)
85
92
84
90
84
80
面试成绩(分)
90
88
86
90
80
85
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是 分,众数是 分;?
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)在(2)的条件下,求出其余5名选手的综合成绩,并以综合成绩排序确定前2名人选.
19.(9分)两组数据3,a,2b,5与a,6,b的平均数都是8,将这两组数据合并为一组数据.
(1)求出a,b的值;
(2)求合并后这组数据的众数和中位数.
20.(9分)某射击队教练为了了解队员的训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数(环)
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
(1)求甲命中环数的中位数和乙命中环数的众数;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定;
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”“变小”或“不变”)?
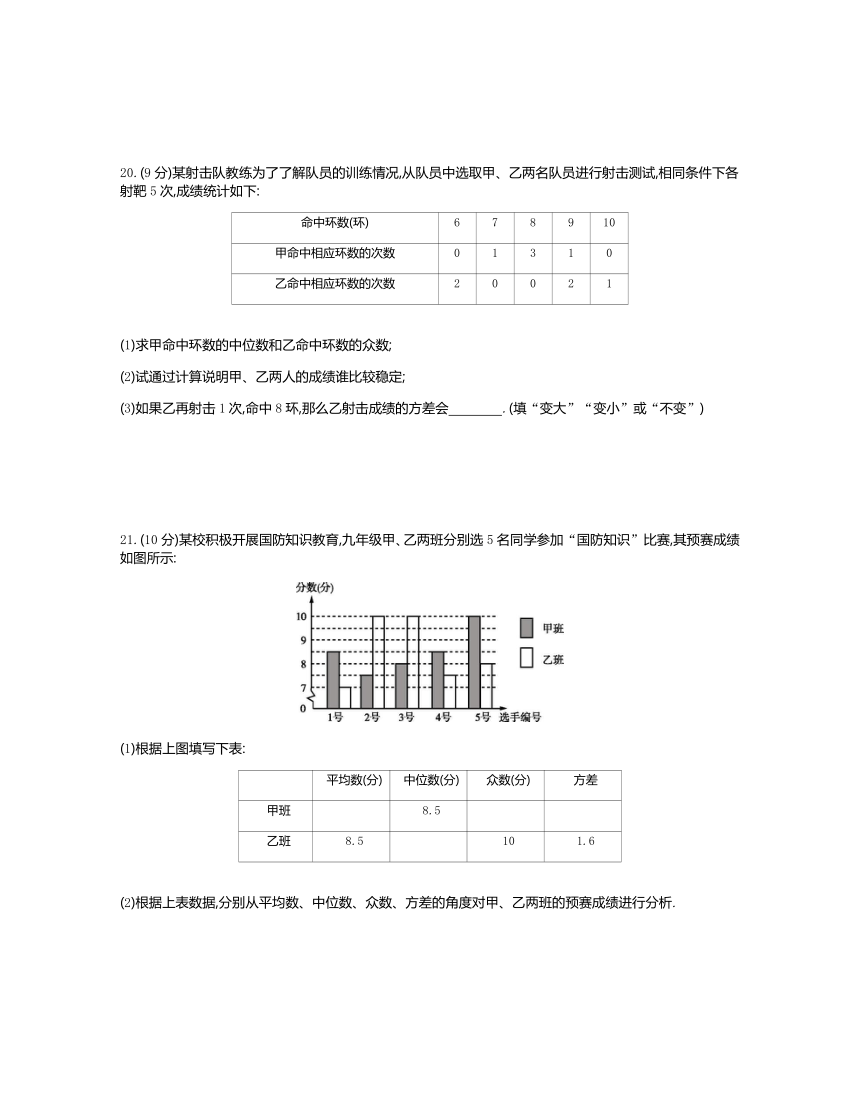
21.(10分)某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据上图填写下表:
平均数(分)
中位数(分)
众数(分)
方差
甲班
8.5
乙班
8.5
10
1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲、乙两班的预赛成绩进行分析.
22.(11分)甲、乙两校参加县教育局举办的2020年学生汉字听写大赛,且两校参赛人数相等.比赛结束后,学生成绩分别为7分、8分、9分、10分(满分为10分),依据统计数据绘制了如下尚不完整的统计图表:
甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
8
(1)在图1中,“7分”所在扇形的圆心角等于 °;请你将甲校成绩统计表和图2的乙校成绩条形统计图补充完整;?
(2)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数,并从平均分和中位数的角度分析哪个学校成绩较好;
(3)如果县教育局要组织一个8人的代表队参加市汉字听写大赛,为了便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
23.(12分)某校举办了一次环保知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩的条形统计图如图所示.
(1)补充完成下面的成绩统计分析表:
组别
平均数(分)
中位数(分)
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)?
(3)甲组学生说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
C
D
C
A
B
11.7 12.90分 13.6,8 14.4 15.4
16.(1)小明一共调查的家庭户数是1+1+3+6+4+2+2+1=20.
(2)因为在这组数据中,4出现了6次,出现的次数最多,
所以这组数据的众数是4.
因为将这组数据按从小到大的顺序排列,其中处于最中间的两个数的平均数是4+42=4,
所以这组数据的中位数是4.
这组数据的平均数是120×(1×1+2×1+3×3+4×6+5×4+6×2+7×2+8×1)=4.5.
故所调查家庭3月份用水量的众数为4吨,中位数为4吨,平均数为4.5吨.
17.(1)甲车间生产的零件直径的中位数在180~184小组内,乙车间生产的零件直径的中位数在175~179小组内,但众数不一定在其相应的小组内,众数是出现次数最多的数,这里只列举出每组中数据的个数,没有给出每个数据具体是多少,不能确定众数会落在哪个小组.
(2)甲车间生产的零件直径合格率为710×100=70%,乙车间生产的零件直径合格率为810×100%=80%,70%<80%.
所以乙车间生产的零件直径合格率高.
18.(1)84.5 84
把这组数据按从小到大的顺序排列为80,84,84,85,90,92,
最中间两个数的平均数是(84+85)÷2=84.5,
则这6名选手笔试成绩的中位数是84.5分.
因为84出现了2次,出现的次数最多,所以这6名选手笔试成绩的众数是84分.
(2)设笔试成绩和面试成绩占的百分比分别是x,1-x,
根据题意得85x+90(1-x)=88,解得x=0.4,
所以笔试成绩和面试成绩占的百分比分别是40%,60%.
(3)2号选手的综合成绩为92×0.4+88×0.6=89.6(分),
3号选手的综合成绩为84×0.4+86×0.6=85.2(分),
4号选手的综合成绩为90×0.4+90×0.6=90(分),
5号选手的综合成绩为84×0.4+80×0.6=81.6(分),
6号选手的综合成绩为80×0.4+85×0.6=83(分),
所以前2名的人选是4号和2号.
19.(1)∵两组数据3,a,2b,5与a,6,b的平均数都是8,
∴a+2b=32-3-5,a+b=24-6,
解得a=12,b=6.
(2)若将这两组数据合并为一组数据,按从小到大的顺序排列为3,5,6,6,12,12,12,
一共7个数,第4个数是6,∴这组数据的中位数是6,
12出现了3次,出现的次数最多,∴众数为12.
20.(1)把甲命中的环数(单位:环)从小到大排列为7,8,8,8,9,这组数据最中间的数是8,所以甲命中环数的中位数是8环;
在乙命中的环数中,6和9都出现了2次,出现的次数最多,则乙命中环数的众数是6环和9环.
(2)甲命中环数的平均数是(7+8+8+8+9)÷5=8(环),
则甲命中环数的方差是15×[(7-8)2+3×(8-8)2+(9-8)2]=0.4,
乙命中环数的平均数是(6+6+9+9+10)÷5=8(环),
则乙命中环数的方差是15×[2×(6-8)2+2×(9-8)2+(10-8)2]=2.8.
因为0.4<2.8,
所以甲的成绩比较稳定.
(3)变小
21.(1)甲班预赛成绩的平均数是(8.5+7.5+8+8.5+10)÷5=8.5(分).
因为8.5出现了2次,出现的次数最多,
所以甲班预赛成绩的众数为8.5分,
s甲2=15×[(8.5-8.5)2+(7.5-8.5)2+(8-8.5)2+(8.5-8.5)2+(10-8.5)2]=0.7.
乙班预赛成绩的中位数是8分.
填写完整的表格如下:
平均数(分)
中位数(分)
众数(分)
方差
甲班
8.5
8.5
8.5
0.7
乙班
8.5
8
10
1.6
(2)从平均数看,两班预赛成绩的平均数相同,则甲、乙两班的成绩一样高;
从中位数看,甲班预赛成绩的中位数大,所以甲班的成绩较好;
从众数看,乙班预赛成绩的众数大,所以乙班的成绩较好;
从方差看,甲班预赛成绩的方差小,所以甲班的成绩更稳定.
22.(1)144
由题意可得,乙校参赛的总人数为4÷72360=20.
题图1中,“7分”所在扇形的圆心角等于360°×820=144°,甲校得9分的人数为20-(11+0+8)=1,乙校得8分的人数为20×54360=3.
补全的甲校成绩统计表如下:
甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
1
8
补全的乙校成绩条形统计图如图所示:
(2)甲校成绩的平均数为120(7×11+8×0+9×1+10×8)=8.3(分),
将甲校成绩从低到高排列,第10个与第11个成绩都是7分,
故甲校成绩的中位数为12(7+7)=7(分).
由于两校的平均分相等,乙校成绩的中位数大于甲校成绩的中位数,
所以从平均分和中位数的角度分析,乙校的成绩较好.
(3)因为要选8名学生参加市汉字听写大赛,甲校得10分的有8人,而乙校得10分的只有5人,所以应选甲校.
23.(1)甲组学生的成绩(单位:分)分别为3,6,6,6,6,6,7,8,9,10,易知中位数为6分,乙组学生成绩的平均数为5×2+6×1+7×2+8×4+9×110=7.1(分).
故补充完整的成绩统计分布表如下:
组别
平均数(分)
中位数(分)
方差
合格率
优秀率
甲组
6.7
6
3.41
90%
20%
乙组
7.1
7.5
1.69
80%
10%
(2)甲
(3)①乙组学生的平均分高于甲组;②乙组学生成绩的方差小,比甲组稳定.(答案不唯一)
一、选择题(本大题共10个小题,每题3分,共30分)
1.某同学参加数学、物理、化学三科竞赛,平均成绩是93分,其中数学97分,化学89分,那么物理成绩是( )
A.91分 B.92分 C.93分 D.94分
2.统计学校排球队员的年龄,结果如下表:
年龄(岁)
12
13
14
15
人数
2
4
6
8
根据表中信息可以判断该学校排球队员的平均年龄为( )
A.13岁 B.14岁 C.13.5岁 D.15岁
3.下列说法错误的是( )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
4.对于一组统计数据3,3,6,5,3,下列说法错误的是( )
A.众数是3 B.平均数是4 C.方差是1.6 D.中位数是6
5.为落实中央扶贫攻坚工作,实施精准扶贫方略,广泛动员全社会力量参与扶贫,校团委开展爱心捐款活动,将某班50名学生捐款情况绘制成了统计图(如图),根据图中提供的信息,此次捐款的众数和中位数分别是( )
A.20元、20元 B.30元、20元 C. 30元、30元 D.20元、30元
第5题图 第6题图
6.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调查结果绘制成如图所示的条形统计图和扇形统计图.根据图中信息,这些学生成绩的平均数和中位数分别是( )
A.2.95分、10分 B.2.5分、2分 C.2.95分、3分 D.3分、4分
7.如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( )
A.甲的数学成绩高于班级平均分,且成绩比较稳定
B.乙的数学成绩在班级平均分附近波动,且比丙好
C.丙的数学成绩低于班级平均分,但成绩逐次提高
D.就甲、乙、丙三个人而言,乙的数学成绩最不稳定
8.某校合唱团有30名成员,合唱团成员的年龄分布统计表如下:
年龄(岁)
13
14
15
16
频数
5
15
x
10-x
则对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数 B.平均数、方差 C.众数、中位数 D.众数、方差
9.在某次考试中,甲、乙、丙、丁四位同学的数学成绩(百分制)分别为85分,90分,x分,80分,若这组数据的众数与平均数相等,则这组数据的中位数是( )
A.85 B.90 C.80 D.70
10.甲、乙两班举行电脑汉字输入比赛,参赛学生人数及每分钟输入汉字的个数经统计计算后的结果如下表:
班级
参加人数
中位数(个)
方差
平均数(个)
甲
55
149
191
135
乙
55
151
110
135
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀(每分钟输入汉字个数大于等于150为优秀)的人数多于甲班优秀的人数;③甲班成绩的波动比乙班成绩的波动小.
上述结论中正确的是( )
A.①②③ B.①② C.①③ D.②③
二、填空题(本大题共5个小题,每题3分,共15分)
11.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
一周在校的体育锻炼时间(h)
5
6
7
8
人数
2
5
6
2
那么这15名学生这一周在校的体育锻炼时间的众数是 h.?
12.在学校的卫生检查中,规定各班的教室桌面和黑板卫生成绩占30%,地面卫生成绩占40%,个人卫生成绩占30%.八年级(1)班这三项成绩分别为85分,90分和95分,则该班卫生检查的总成绩为 .?
13.已知一组数据x1,x2,x3的平均数是5,方差是2,那么另一组数据2x1-4,2x2-4,2x3-4的平均数和方差分别是 .?
14.若3,a,4,5的众数是4,则这组数据的平均数是 .?
15.已知20个数据的平均数为6,且这20个数据的平方和为800,则这组数据的方差等于 .?
三、解答题(本大题共8个小题,共75分)
16.(8分)为了宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数.
17.(8分)某厂为了检验甲、乙两车间生产的同一种零件的直径(单位:mm)的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:
170~174
175~179
180~184
185~189
甲车间
1
3
4
2
乙车间
0
6
2
2
(1)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(2)若该零件的直径在175~184 mm的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
18.(8分)某单位招聘员工,采取笔试与面试相结合的方式,两项成绩的原始分均为100分.前6名选手的得分如下:
项目序号
1
2
3
4
5
6
笔试成绩(分)
85
92
84
90
84
80
面试成绩(分)
90
88
86
90
80
85
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是 分,众数是 分;?
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)在(2)的条件下,求出其余5名选手的综合成绩,并以综合成绩排序确定前2名人选.
19.(9分)两组数据3,a,2b,5与a,6,b的平均数都是8,将这两组数据合并为一组数据.
(1)求出a,b的值;
(2)求合并后这组数据的众数和中位数.
20.(9分)某射击队教练为了了解队员的训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数(环)
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
(1)求甲命中环数的中位数和乙命中环数的众数;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定;
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”“变小”或“不变”)?
21.(10分)某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据上图填写下表:
平均数(分)
中位数(分)
众数(分)
方差
甲班
8.5
乙班
8.5
10
1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲、乙两班的预赛成绩进行分析.
22.(11分)甲、乙两校参加县教育局举办的2020年学生汉字听写大赛,且两校参赛人数相等.比赛结束后,学生成绩分别为7分、8分、9分、10分(满分为10分),依据统计数据绘制了如下尚不完整的统计图表:
甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
8
(1)在图1中,“7分”所在扇形的圆心角等于 °;请你将甲校成绩统计表和图2的乙校成绩条形统计图补充完整;?
(2)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数,并从平均分和中位数的角度分析哪个学校成绩较好;
(3)如果县教育局要组织一个8人的代表队参加市汉字听写大赛,为了便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
23.(12分)某校举办了一次环保知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩的条形统计图如图所示.
(1)补充完成下面的成绩统计分析表:
组别
平均数(分)
中位数(分)
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)?
(3)甲组学生说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
C
D
C
A
B
11.7 12.90分 13.6,8 14.4 15.4
16.(1)小明一共调查的家庭户数是1+1+3+6+4+2+2+1=20.
(2)因为在这组数据中,4出现了6次,出现的次数最多,
所以这组数据的众数是4.
因为将这组数据按从小到大的顺序排列,其中处于最中间的两个数的平均数是4+42=4,
所以这组数据的中位数是4.
这组数据的平均数是120×(1×1+2×1+3×3+4×6+5×4+6×2+7×2+8×1)=4.5.
故所调查家庭3月份用水量的众数为4吨,中位数为4吨,平均数为4.5吨.
17.(1)甲车间生产的零件直径的中位数在180~184小组内,乙车间生产的零件直径的中位数在175~179小组内,但众数不一定在其相应的小组内,众数是出现次数最多的数,这里只列举出每组中数据的个数,没有给出每个数据具体是多少,不能确定众数会落在哪个小组.
(2)甲车间生产的零件直径合格率为710×100=70%,乙车间生产的零件直径合格率为810×100%=80%,70%<80%.
所以乙车间生产的零件直径合格率高.
18.(1)84.5 84
把这组数据按从小到大的顺序排列为80,84,84,85,90,92,
最中间两个数的平均数是(84+85)÷2=84.5,
则这6名选手笔试成绩的中位数是84.5分.
因为84出现了2次,出现的次数最多,所以这6名选手笔试成绩的众数是84分.
(2)设笔试成绩和面试成绩占的百分比分别是x,1-x,
根据题意得85x+90(1-x)=88,解得x=0.4,
所以笔试成绩和面试成绩占的百分比分别是40%,60%.
(3)2号选手的综合成绩为92×0.4+88×0.6=89.6(分),
3号选手的综合成绩为84×0.4+86×0.6=85.2(分),
4号选手的综合成绩为90×0.4+90×0.6=90(分),
5号选手的综合成绩为84×0.4+80×0.6=81.6(分),
6号选手的综合成绩为80×0.4+85×0.6=83(分),
所以前2名的人选是4号和2号.
19.(1)∵两组数据3,a,2b,5与a,6,b的平均数都是8,
∴a+2b=32-3-5,a+b=24-6,
解得a=12,b=6.
(2)若将这两组数据合并为一组数据,按从小到大的顺序排列为3,5,6,6,12,12,12,
一共7个数,第4个数是6,∴这组数据的中位数是6,
12出现了3次,出现的次数最多,∴众数为12.
20.(1)把甲命中的环数(单位:环)从小到大排列为7,8,8,8,9,这组数据最中间的数是8,所以甲命中环数的中位数是8环;
在乙命中的环数中,6和9都出现了2次,出现的次数最多,则乙命中环数的众数是6环和9环.
(2)甲命中环数的平均数是(7+8+8+8+9)÷5=8(环),
则甲命中环数的方差是15×[(7-8)2+3×(8-8)2+(9-8)2]=0.4,
乙命中环数的平均数是(6+6+9+9+10)÷5=8(环),
则乙命中环数的方差是15×[2×(6-8)2+2×(9-8)2+(10-8)2]=2.8.
因为0.4<2.8,
所以甲的成绩比较稳定.
(3)变小
21.(1)甲班预赛成绩的平均数是(8.5+7.5+8+8.5+10)÷5=8.5(分).
因为8.5出现了2次,出现的次数最多,
所以甲班预赛成绩的众数为8.5分,
s甲2=15×[(8.5-8.5)2+(7.5-8.5)2+(8-8.5)2+(8.5-8.5)2+(10-8.5)2]=0.7.
乙班预赛成绩的中位数是8分.
填写完整的表格如下:
平均数(分)
中位数(分)
众数(分)
方差
甲班
8.5
8.5
8.5
0.7
乙班
8.5
8
10
1.6
(2)从平均数看,两班预赛成绩的平均数相同,则甲、乙两班的成绩一样高;
从中位数看,甲班预赛成绩的中位数大,所以甲班的成绩较好;
从众数看,乙班预赛成绩的众数大,所以乙班的成绩较好;
从方差看,甲班预赛成绩的方差小,所以甲班的成绩更稳定.
22.(1)144
由题意可得,乙校参赛的总人数为4÷72360=20.
题图1中,“7分”所在扇形的圆心角等于360°×820=144°,甲校得9分的人数为20-(11+0+8)=1,乙校得8分的人数为20×54360=3.
补全的甲校成绩统计表如下:
甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
1
8
补全的乙校成绩条形统计图如图所示:
(2)甲校成绩的平均数为120(7×11+8×0+9×1+10×8)=8.3(分),
将甲校成绩从低到高排列,第10个与第11个成绩都是7分,
故甲校成绩的中位数为12(7+7)=7(分).
由于两校的平均分相等,乙校成绩的中位数大于甲校成绩的中位数,
所以从平均分和中位数的角度分析,乙校的成绩较好.
(3)因为要选8名学生参加市汉字听写大赛,甲校得10分的有8人,而乙校得10分的只有5人,所以应选甲校.
23.(1)甲组学生的成绩(单位:分)分别为3,6,6,6,6,6,7,8,9,10,易知中位数为6分,乙组学生成绩的平均数为5×2+6×1+7×2+8×4+9×110=7.1(分).
故补充完整的成绩统计分布表如下:
组别
平均数(分)
中位数(分)
方差
合格率
优秀率
甲组
6.7
6
3.41
90%
20%
乙组
7.1
7.5
1.69
80%
10%
(2)甲
(3)①乙组学生的平均分高于甲组;②乙组学生成绩的方差小,比甲组稳定.(答案不唯一)
