华东师大版七年级上册数学学案:4.1生活中的立体图形(无答案)
文档属性
| 名称 | 华东师大版七年级上册数学学案:4.1生活中的立体图形(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 14:21:29 | ||
图片预览

文档简介
4.1生活中的立体图形
导学目标:
1、知识与能力
1.认识什么是柱体、锥体、球体及多面体.
2、过程与方法
1.能把生活中的立体图形抽象成几何图形.
3、情感、态度与价值观
1.提高空间想象能力,培养好奇心和求知欲.
导学重点难点:
1.感受图形世界的丰富多彩.
2.认识圆柱、圆锥、正方体、长方体、棱柱、球,并能用自己的语言描述它们得到某种特征.
导学过程:
问题探究:在小学中我们已学过哪些图形?你能把它们分类吗?它们各有什么特点?
合作交流:生1:小学学过许多图形,如:长方形、正方形、三角形、梯形、平行四边形、圆等.
生2:我们还学过正方体、长方体.
生3:前面两个同学说的图形是不同的两类图形,前者是平面图形,后者是立体图形. 学了本节你将会知道更多的立体图形!
教材知识
知识点1 生活中常见的立体图形及其分类
立体图形是从实物中抽象出的数学模型,如图4—1—1所示是生活中常见的立体图形.
253365099060
立体图形主要分为柱体、锥体、球体.
1. 柱体分为两类:一类是圆柱,如图4—1—1(7)所示,一类是棱柱,如图4—1—1(1)(2)(3)(4)所示.
(1)柱体的上、下底面是两个完全相同的面,圆柱的底面是圆,棱柱的底面是多边形.
(2)棱柱可按底面多边形的边数分为三棱柱、四棱柱、…、n棱柱.
2. 锥体也分为两类:一类是圆锥,如图4—1—1(8)所示,一类是棱锥,如图4—1—1(5)(6)所示.
(1)圆锥的底面是圆,棱锥的底面是多边形.
473392599060(2)棱锥可按底面多边形的边数分为三棱锥、四棱锥、…、n棱锥.
3. 球体由一个曲面围成. 如图4—1—1(9)所示.
注意:(1)立体图形是由一个或几个面围成的,例如,球只由一个面围成,而长方体由六个面围成.
(2)组成棱柱与棱锥的面是平的,而组成圆锥、圆柱、球的面中有曲的.
知识点2 多面体
由平面围成的立体图形称为多面体.
注意:(1)多面体中围成立体图形的面都是平面,如棱柱、棱锥,没有曲面,而圆柱、圆锥的侧面及球的表面是曲面,所以它们都不是多面体.
(2)多面体根据组成这个立体图形的面数决定是几面体,如正方体、长方体都是六面体,五棱锥也是六面体.
课堂检测
基本概念题
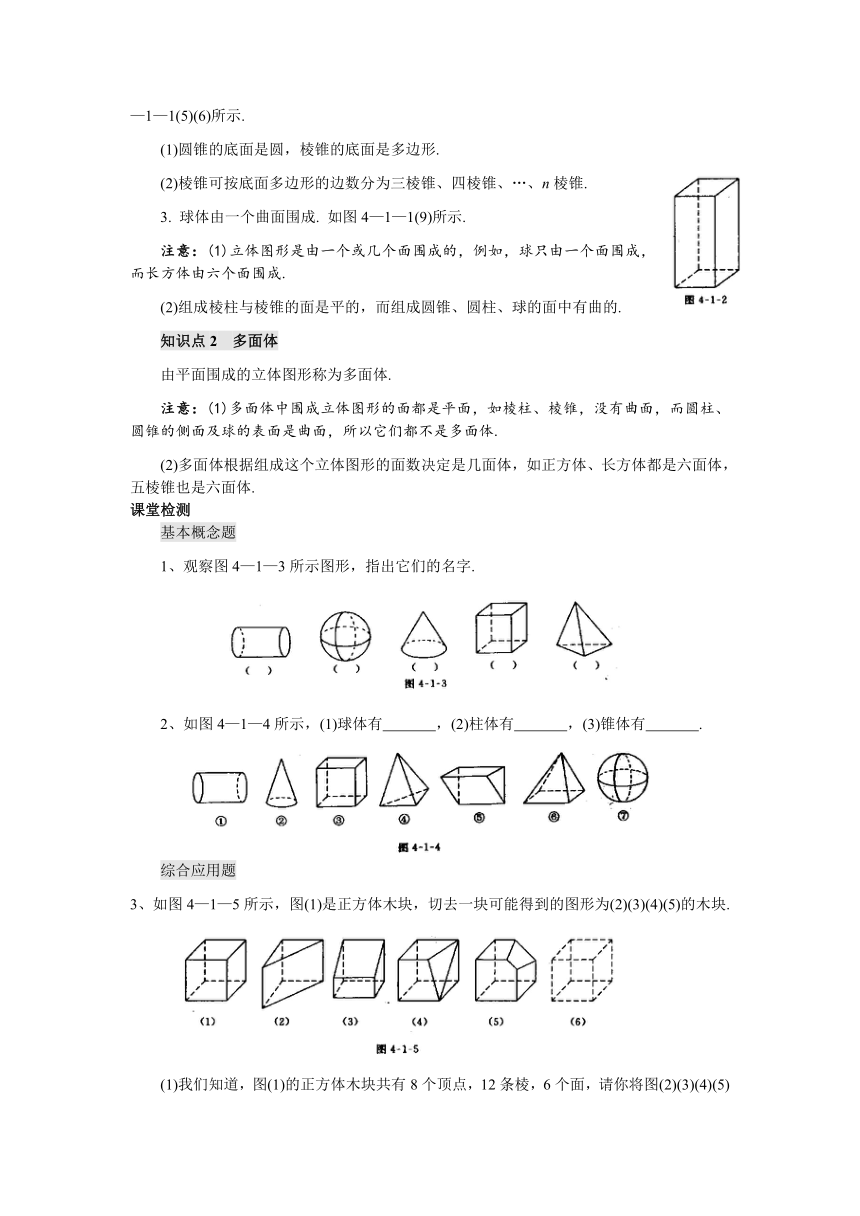
1、观察图4—1—3所示图形,指出它们的名字.
2、如图4—1—4所示,(1)球体有 ,(2)柱体有 ,(3)锥体有 .
综合应用题
3、如图4—1—5所示,图(1)是正方体木块,切去一块可能得到的图形为(2)(3)(4)(5)的木块.
(1)我们知道,图(1)的正方体木块共有8个顶点,12条棱,6个面,请你将图(2)(3)(4)(5)中的木块的顶点数、棱数、面数填入下表.
图
顶点数(V)
棱数(E)
面数(F)
(1)
8
12
6
(2)
(3)
(4)
(5)
(2)观察上表,请你归纳上述各种木块的顶点数、棱数、面数之间的关系,这种数量关系为 .
(3)图(6)是用虚线画的正方体木块. 请你想象一种与图(2)(3)(4)(5)不同的切法,则切去一块后得到的一块木块的顶点数为 ,棱数为 ,面数为 . 这与你在第(2)题中归纳的关系是否相符?
4、如图4—1—7所示,分别指出下列物体的形状类似于哪种立体图形.
探索创新题
5、下列图形绕虚线旋转一周,能得到图4—1—8的是( )
体验中考
1、直四棱柱、长方体和正方体之间的包含关系是( )
2、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(v)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式. 请你观察图4-1-9几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
面点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
你发现顶点数(V),面数(F),棱数(E)之间存在的关系式是 ;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 ;
(3)某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱. 设该多面体外表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
导学反思:
本节亮点
2、待改进处
导学目标:
1、知识与能力
1.认识什么是柱体、锥体、球体及多面体.
2、过程与方法
1.能把生活中的立体图形抽象成几何图形.
3、情感、态度与价值观
1.提高空间想象能力,培养好奇心和求知欲.
导学重点难点:
1.感受图形世界的丰富多彩.
2.认识圆柱、圆锥、正方体、长方体、棱柱、球,并能用自己的语言描述它们得到某种特征.
导学过程:
问题探究:在小学中我们已学过哪些图形?你能把它们分类吗?它们各有什么特点?
合作交流:生1:小学学过许多图形,如:长方形、正方形、三角形、梯形、平行四边形、圆等.
生2:我们还学过正方体、长方体.
生3:前面两个同学说的图形是不同的两类图形,前者是平面图形,后者是立体图形. 学了本节你将会知道更多的立体图形!
教材知识
知识点1 生活中常见的立体图形及其分类
立体图形是从实物中抽象出的数学模型,如图4—1—1所示是生活中常见的立体图形.
253365099060
立体图形主要分为柱体、锥体、球体.
1. 柱体分为两类:一类是圆柱,如图4—1—1(7)所示,一类是棱柱,如图4—1—1(1)(2)(3)(4)所示.
(1)柱体的上、下底面是两个完全相同的面,圆柱的底面是圆,棱柱的底面是多边形.
(2)棱柱可按底面多边形的边数分为三棱柱、四棱柱、…、n棱柱.
2. 锥体也分为两类:一类是圆锥,如图4—1—1(8)所示,一类是棱锥,如图4—1—1(5)(6)所示.
(1)圆锥的底面是圆,棱锥的底面是多边形.
473392599060(2)棱锥可按底面多边形的边数分为三棱锥、四棱锥、…、n棱锥.
3. 球体由一个曲面围成. 如图4—1—1(9)所示.
注意:(1)立体图形是由一个或几个面围成的,例如,球只由一个面围成,而长方体由六个面围成.
(2)组成棱柱与棱锥的面是平的,而组成圆锥、圆柱、球的面中有曲的.
知识点2 多面体
由平面围成的立体图形称为多面体.
注意:(1)多面体中围成立体图形的面都是平面,如棱柱、棱锥,没有曲面,而圆柱、圆锥的侧面及球的表面是曲面,所以它们都不是多面体.
(2)多面体根据组成这个立体图形的面数决定是几面体,如正方体、长方体都是六面体,五棱锥也是六面体.
课堂检测
基本概念题
1、观察图4—1—3所示图形,指出它们的名字.
2、如图4—1—4所示,(1)球体有 ,(2)柱体有 ,(3)锥体有 .
综合应用题
3、如图4—1—5所示,图(1)是正方体木块,切去一块可能得到的图形为(2)(3)(4)(5)的木块.
(1)我们知道,图(1)的正方体木块共有8个顶点,12条棱,6个面,请你将图(2)(3)(4)(5)中的木块的顶点数、棱数、面数填入下表.
图
顶点数(V)
棱数(E)
面数(F)
(1)
8
12
6
(2)
(3)
(4)
(5)
(2)观察上表,请你归纳上述各种木块的顶点数、棱数、面数之间的关系,这种数量关系为 .
(3)图(6)是用虚线画的正方体木块. 请你想象一种与图(2)(3)(4)(5)不同的切法,则切去一块后得到的一块木块的顶点数为 ,棱数为 ,面数为 . 这与你在第(2)题中归纳的关系是否相符?
4、如图4—1—7所示,分别指出下列物体的形状类似于哪种立体图形.
探索创新题
5、下列图形绕虚线旋转一周,能得到图4—1—8的是( )
体验中考
1、直四棱柱、长方体和正方体之间的包含关系是( )
2、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(v)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式. 请你观察图4-1-9几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
面点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
你发现顶点数(V),面数(F),棱数(E)之间存在的关系式是 ;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 ;
(3)某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱. 设该多面体外表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
导学反思:
本节亮点
2、待改进处
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
