2020-2021学年北师大初一上数学6.3数据的表示检测练习(word解析版)
文档属性
| 名称 | 2020-2021学年北师大初一上数学6.3数据的表示检测练习(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 248.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-21 00:00:00 | ||
图片预览



文档简介
2020-2021学年北师大初一上数学6.3数据的表示检测练习
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分)
在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组所占的百分比之和为,则第5组的频数是
A.
9
B.
10
C.
8
D.
7
将40个统计数据分成6组,若某一组的频率为,则该组的频数为
A.
6
B.
C.
D.
1
下列说法:条形统计图就是频数分布直方图条形统计图各个“条形”之间有间隙,而频数分布直方图没有频数分布直方图用横轴表示考察对象数据的变化范围,用纵轴表示相应范围内数据的频数其中正确的是?
?
A.
B.
C.
D.
在n个数据的频数分布直方图中,下列结论成立的是
A.
各小组频率之和等于n
B.
各小组频数之和等于1
C.
各小组频数之和等于n
D.
各小组长方形高的和等于1
频率分布直方图的纵轴表示
A.
B.
C.
D.
某中学为了调查不同面额纸币上的细菌数量与使用次数的关系,分别从银行、商店、农贸市场及医院收费处随机采集了6种面额的纸币各30张,分别用无菌生理盐水漂洗这些纸币,对洗出液进行细菌培养,测得数据如下表:
面额
5角
1元
5元
10元
50元
100元
细菌总数
个张
147400
381150
98800
145500
25700
12250
这组数据获得的方法为?
???
A.
直接观察
B.
调查
C.
互联网查询
D.
实验
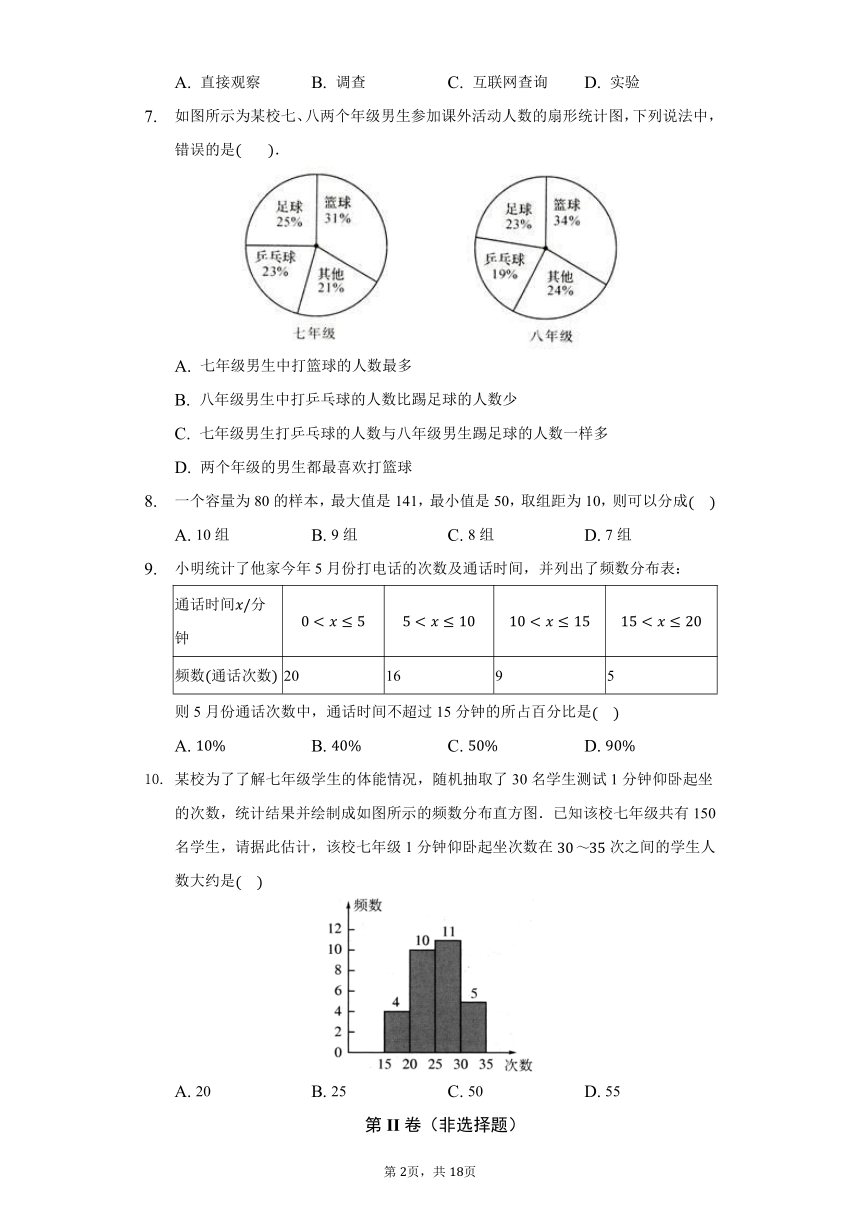
如图所示为某校七、八两个年级男生参加课外活动人数的扇形统计图,下列说法中,错误的是?
?
?.
A.
七年级男生中打篮球的人数最多
B.
八年级男生中打乒乓球的人数比踢足球的人数少
C.
七年级男生打乒乓球的人数与八年级男生踢足球的人数一样多
D.
两个年级的男生都最喜欢打篮球
一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分成
A.
10组
B.
9组
C.
8组
D.
7组
小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间分钟
频数通话次数
20
16
9
5
则5月份通话次数中,通话时间不超过15分钟的所占百分比是
A.
B.
C.
D.
某校为了了解七年级学生的体能情况,随机抽取了30名学生测试1分钟仰卧起坐的次数,统计结果并绘制成如图所示的频数分布直方图.已知该校七年级共有150名学生,请据此估计,该校七年级1分钟仰卧起坐次数在次之间的学生人数大约是
A.
20
B.
25
C.
50
D.
55
第II卷(非选择题)
二、填空题(本大题共4小题,共16.0分)
已知全班共有40名学生,他们上学有的步行,有的骑车,还有的乘车其中步行的频数是13,骑车的频数是11,则乘车的频率是_____.
一只不透明的袋子中装有红球和白球50个,这些球除了颜色外都相同,某个学习小组做摸球试验,将球搅匀后任意摸出一个球,记下颜色后放回、搅匀,通过多次重复试验,算得摸到红球的频率是,则袋中有______个红球.
在一个样本容量为80的样本所绘制的频数分布直方图中,4个小组所对应的各个长方形高的比为2:3:4:1,那么第二组频数是______.
武侯区某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据单位:分钟:10、12、15、8、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、若将这些数据以4为组距进行分组,则组数是_____组.
三、解答题(本大题共6小题,共54.0分)
七年级320名学生参加安全知识竞赛活动,小明随机调查了部分学生的成绩分数为整数,绘制了频率分布表和频数分布直方图不完整,请结合图表信息回答下列问题:
成绩分
频数
2
8
12
10
6
2
补全频数直方图;
小明调查的学生人数是______;频率分布表的组距是______;
七年级参加本次竞赛活动,分数x在范围内的学生约有多少人.
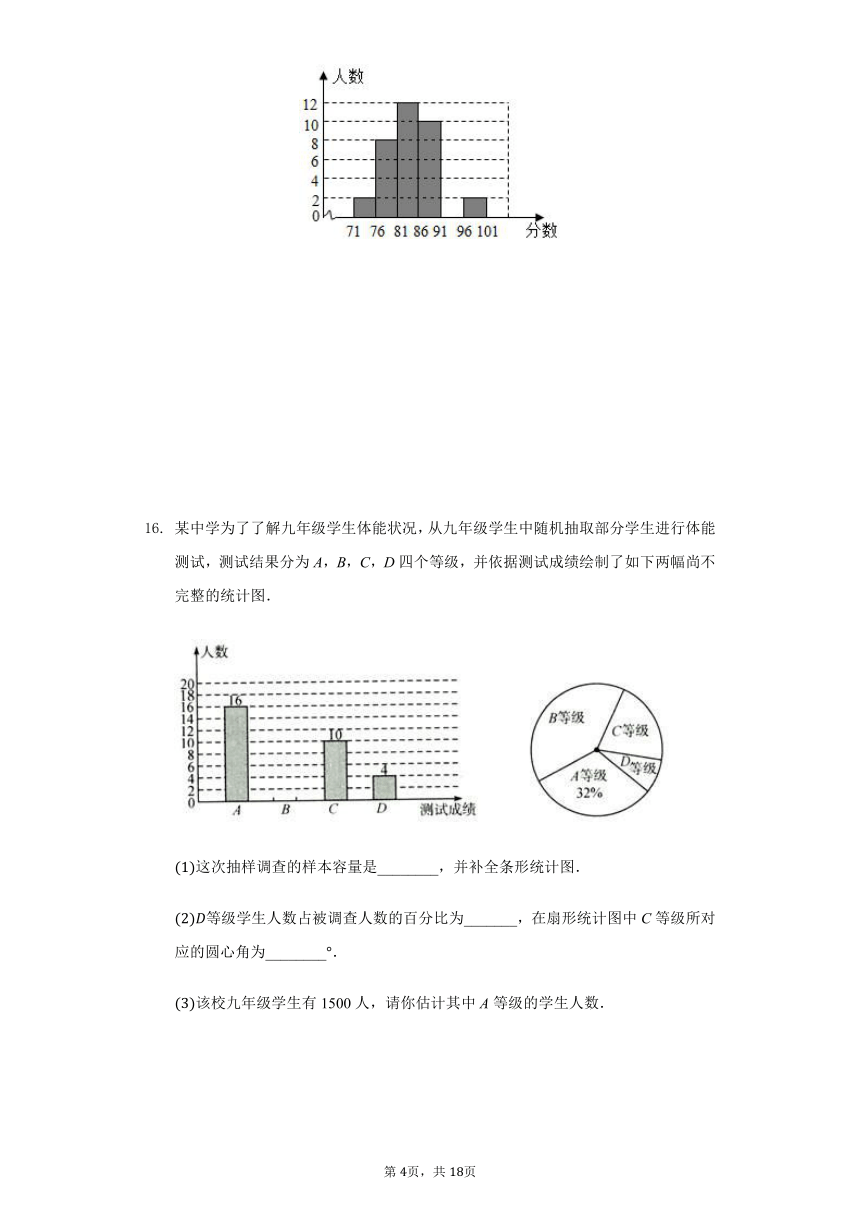
某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图.
这次抽样调查的样本容量是________,并补全条形统计图.
等级学生人数占被调查人数的百分比为_______,在扇形统计图中C等级所对应的圆心角为________.
该校九年级学生有1500人,请你估计其中A等级的学生人数.
垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某校举行一场学生在线参与垃圾分类处理知识测试满分100分,得分均为整数,学校从全校2800名学生中随机抽取部分学生的成绩,绘制成如图不完整的统计图表.
抽取的部分学生测试成绩的频数分布表
成绩分
频数人
百分比
10
15
n
m
40
15
由图表中给出的信息回答下列问题:
频数分布表中,_____,_____本次抽样调查的样本容量是_____.
补全频数分布直方图.
如果成绩在80分以上包括80分为优秀,估计该校本次测试成绩优秀的学生人数.
体育委员统计了全班同学60秒跳绳的次数,绘制出频数分布表和部分频数分布直方图,如图所示.请根据以下信息,解答下列问题:
次数x
频数
2
4
20
12
8
3
1
Ⅰ补全直方图;
Ⅱ全班有学生______名,频数分布表的组距是______,组数是______;
Ⅲ跳绳次数x在范围内的学生有______,占全班学生的百分之______。
某校八年级学生进行体育测试,八年级班男生的立定跳远成绩绘制成如图所示的频数分布直方图,图中从左到右各矩形的高之比是,最后一组的频数是6,根据直方图所表达的信息,解答下列问题.
该班有多少名男生?
若立定跳远的成绩在以上包括为合格,则该班的这项测试合格率是多少?
“微信运动“被越来越多的人关注和喜爱,某兴趣小组随机调查了某市50名教师某日微信运动中的步数情况并进行统计整理,绘制了如图的统计图表不完整,请根据以上信息,解答下列问题:
组别
步数万步
频
第1组
8
第2组
15
第3组
12
第4组
10
第5组
3
第6组
a
______,______;
补全频数分布直方图;
若该市约有40000名教师,估计日行走步数超过万步包含万步的教师约有多少名?
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查频数与频率,解题的关键是掌握频数之和等于总数、频率之和等于1,频率频数总数根据频率之和等于1求得第5组的频率,再由频数频率总数计算可得.
【解答】
解:第一组到第四组所占的百分比之和为,
第五组的所占的百分比之为,
则第五组的频数为.
故选B.
2.【答案】A
【解析】
【分析】
本题考查频率公式.根据频率公式:,频数频率总数,把频率,总数代入计算即可.
【解答】
解:,
频数频率总数.
故选A.
3.【答案】B
【解析】
【分析】本题主要考查条形统计图与频数分布直方图之间的关系,只要重点掌握其各自的特点,再加以区分即可解答,频数分布直方图条与条之间无间隔,而条形统计图有;条形统计图是用条形的高度表示频数的大小,而直方图是用长方形的面积表示频数,当长方形的宽相等的时候,把组距看成“1”,用矩形的的高表示频数;根据这些作判断即可.
【解答】
解:条形图是用条形的高度表示频数的大小,而直方图实际上是用长方形的面积表示频数,二者有很大的区别,故错误;
条形统计图各个“条形”之间有间隙,而频数分布直方图没有,故描述正确;
频数分布直方图用横轴表示考察对象数据的变化范围,用纵轴表示相应范围内数据的频数,故描述正确;
故选B.
4.【答案】C
【解析】
【分析】
本题主要考查了频数分布直方图,解答此题的关键是弄清频数分布直方图的横坐标与纵坐标表示的意义,解答此题根据频数分布直方图的意义解答即可.
【解答】
解:各小组的频率之和应等于1,故错误;
B.各小组的频数之和应等于总数据n,故错误;
C.各小组频数之和等于n,正确;
D.各小组的长方形高的和不是1,故错误.
故选C.
5.【答案】A
【解析】解:频率分布直方图的纵轴表示,
故选:A.
根据频率分布直方图中纵横坐标的意义即可得.
本题考查频率直方图中横纵坐标表示的意义.
6.【答案】D
【解析】
【分析】
此题考查了数据的获取方法,实验法.分别从不同的地方获取一定数量的实验数据,注意数学知识和生活实际的联系.
【解答】
解:为了调查不同面额纸币上的细菌数量与使用次数的关系,分别从银行、商店、农贸市场及医院收费处随机采集了6种面额的纸币各30张,得到数据,这种方法为实验法.
故选D.
7.【答案】C
【解析】
【分析】
本题考查扇形统计图的知识,比较简单,解答本题的关键是充分理解扇形统计图的特点,扇形统计图只能反应所占某个总体的百分比,不能判断具体数量.观察扇形统计图,扇形统计图反应了七、八年级男生参加各种课外活动的人数占总人数的百分比,不能具体判断不同年级参加某项课外活动的人数多少.
【解答】
解:由题意可得本题的各年级的男生人数无法确定,故不能确定七年级男生打乒乓球与八年级男生踢足球的具体人数.
所以C选项错误.
故选C.
8.【答案】A
【解析】
【分析】
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数最大值最小值组距计算,注意小数部分要进位.
【解答】
解:在样本数据中最大值为141,最小值为50,它们的差是,
已知组距为10,那么由于,
故可以分成10组.
故选A.
9.【答案】D
【解析】解:5月份通话次数中,通话时间不超过15分钟的所占百分比是,
故选:D.
根据表格可以得到总的频数和通话时间不超过15分钟的频数,从而可以求得通话时间不超过15分钟的百分比.
本题考查频数分布表,解题的关键是明确题意,找出所求问题需要的条件.
10.【答案】B
【解析】解:该校九年级1分钟仰卧起坐次数在次之间的学生人数大约是人,
故选:B.
用总人数乘以样本中仰卧起坐次数在次之间的学生人数占被调查人数的比例即可得.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
11.【答案】?
【解析】
【试题解析】
【分析】
本题考查了频数与频率,解题关键是知道各量之间的关系.
由步行的频数是13,骑车的频数是11,从而得到则乘车的频率.
【解答】
解:乘车的频率是:.
故答案为?.
12.【答案】10
【解析】解:一只不透明的袋子中装有红球和白球50个,摸到红球的频率是,
袋中有红球:个.
故答案为:10.
直接利用频率的意义进而分析得出答案.
此题主要考查了频率,正确理解频率的意义是解题关键.
13.【答案】24
【解析】解:.
故答案是:24.
频数分布直方图中,各个长方形的高之比依次为2:3:4:1,则指各组频数之比为2:3:4:1,据此即可求出第二小组的频数.
此题考查了频数率分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.
14.【答案】5
【解析】
【分析】
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数最大值最小值组距计算,注意小数部分要进位.则,所以组数为5.
【解答】
解:根据组数最大值最小值组距小数部分要进位
则
所以组数为5.
故答案为5.
15.【答案】40?
5
【解析】解:由频数分布表可知,
这一组的频数是6,
补全的频数分布直方图如右图所示;
小明调查的学生人数是:,
频率分布表的组距是,
故答案为:40,5;
人,
答:分数x在范围内的学生约有128人.
根据频数分布表中的数据,可以将频数分布直方图补充完整;
根据频数分布表中的数据,可以计算出小明调查的学生人数,再根据直方图中的数据,可以计算出组距;
根据频数分布表中的数据,可以计算出分数x在范围内的学生约有多少人.
本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
16.【答案】解:;
补全条形图如图所示:
;
;72;
该校九年级学生有1500人,
估计其中A等级的学生人数人.
【解析】
【分析】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
由A等级的人数和其所占的百分比即可求出抽样调查的样本容量;求出B等级的人数即可补全条形图;
用B等级的人数除以总人数即可得到其占被调查人数的百分比;求出C等级所占的百分比,即可求出C等级所对应的圆心角;
由扇形统计图可知A等级所占的百分比,进而可求出九年级学生其中A等级的学生人数.
【解答】
解:由条形统计图和扇形统计图可知总人数人,所以B等级的人数人,
故答案为50;
等级学生人数占被调查人数的百分比;
在扇形统计图中C等级所对应的圆心角,
故答案为;72;
见答案.
17.【答案】解:,,100;
由知,,
补全的频数分布直方图如图所示;
,
人.
答:估计该校本次测试成绩优秀的学生人数为1540人.
【解析】
【试题解析】
【分析】
本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
根据这一组的频数和所占的百分比,可以求得本次抽取的人数,然后即可计算出m、n的值;
根据中m的值,可以将频数分布直方图补充完整;
根据频数分布表中的数据,可以得到成绩为优秀的人数占被抽取人数的百分比,进而得解.
【解答】
解:随机抽取的学生总人数为:,
,
,
故答案为:20,,100;
见答案;
见答案.
18.【答案】解:Ⅰ在有4人,有8人,补全直方图如下:
Ⅱ,20,7;
Ⅲ人,64.
【解析】
【分析】
本题主要考查的是频数分布表和频数分布直方图的应用,能够从统计图和统计表中获取有效信息是解题的关键.
Ⅰ根据频数统计表可知跳绳次数在之间的频数是4,之间的频数为8,从而可补全直方图;
Ⅱ把所有的频数加起来得出全班学生数,再根据图表给出的数据即可得出频数分布表的组距和组数;
Ⅲ把数x在范围内的频数加起来得出次数x在范围内的学生数,再除以总数即可得出占全班学生的百分比.
解:Ⅰ见答案
Ⅱ全班有学生人,
频数分布表的组距是20;组数是7;
故答案为:50,20,7;
Ⅲ?根据题意得:
人,
则跳绳次数x在范围内的学生有32人;
占全班学生人数的百分比是:.
故答案为32人,64.
19.【答案】解:人,即该班有40名男生;
,即立定跳远的成绩在米以上包括米为合格,合格率是.
【解析】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
利用最后一组的频数所占的百分比八年级班男生人数;
用立定跳远的成绩在米以上的人数所占的比例和立定跳远的成绩在米以上包括米的合格率.
20.【答案】2?
16
【解析】,
第1组的占比为,因此.
故答案为:2,16.
画图如下:
根据题意:,和的总人数为:人.
占总人数的比例为:.
因此,全市日行走步数超过万步包含万步的教师约有:
人.
总共调查人数为50,因此,第1组的占比为.
根据求得的a的值画图即可.
需要先计算超过万步的占比,在计算人数.
本题是一道利用统计知识解答实际问题的重点考题,主要考查利用统计图表,处理数据的能力和利用样本估计总体的思想.解答这类题目,观察图表要细致,对应的图例及其关系不能错位,计算要认真准确.同时,解题方法要灵活多样,切忌死记硬背,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.
第18页,共18页
第17页,共18页
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分)
在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组所占的百分比之和为,则第5组的频数是
A.
9
B.
10
C.
8
D.
7
将40个统计数据分成6组,若某一组的频率为,则该组的频数为
A.
6
B.
C.
D.
1
下列说法:条形统计图就是频数分布直方图条形统计图各个“条形”之间有间隙,而频数分布直方图没有频数分布直方图用横轴表示考察对象数据的变化范围,用纵轴表示相应范围内数据的频数其中正确的是?
?
A.
B.
C.
D.
在n个数据的频数分布直方图中,下列结论成立的是
A.
各小组频率之和等于n
B.
各小组频数之和等于1
C.
各小组频数之和等于n
D.
各小组长方形高的和等于1
频率分布直方图的纵轴表示
A.
B.
C.
D.
某中学为了调查不同面额纸币上的细菌数量与使用次数的关系,分别从银行、商店、农贸市场及医院收费处随机采集了6种面额的纸币各30张,分别用无菌生理盐水漂洗这些纸币,对洗出液进行细菌培养,测得数据如下表:
面额
5角
1元
5元
10元
50元
100元
细菌总数
个张
147400
381150
98800
145500
25700
12250
这组数据获得的方法为?
???
A.
直接观察
B.
调查
C.
互联网查询
D.
实验
如图所示为某校七、八两个年级男生参加课外活动人数的扇形统计图,下列说法中,错误的是?
?
?.
A.
七年级男生中打篮球的人数最多
B.
八年级男生中打乒乓球的人数比踢足球的人数少
C.
七年级男生打乒乓球的人数与八年级男生踢足球的人数一样多
D.
两个年级的男生都最喜欢打篮球
一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分成
A.
10组
B.
9组
C.
8组
D.
7组
小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间分钟
频数通话次数
20
16
9
5
则5月份通话次数中,通话时间不超过15分钟的所占百分比是
A.
B.
C.
D.
某校为了了解七年级学生的体能情况,随机抽取了30名学生测试1分钟仰卧起坐的次数,统计结果并绘制成如图所示的频数分布直方图.已知该校七年级共有150名学生,请据此估计,该校七年级1分钟仰卧起坐次数在次之间的学生人数大约是
A.
20
B.
25
C.
50
D.
55
第II卷(非选择题)
二、填空题(本大题共4小题,共16.0分)
已知全班共有40名学生,他们上学有的步行,有的骑车,还有的乘车其中步行的频数是13,骑车的频数是11,则乘车的频率是_____.
一只不透明的袋子中装有红球和白球50个,这些球除了颜色外都相同,某个学习小组做摸球试验,将球搅匀后任意摸出一个球,记下颜色后放回、搅匀,通过多次重复试验,算得摸到红球的频率是,则袋中有______个红球.
在一个样本容量为80的样本所绘制的频数分布直方图中,4个小组所对应的各个长方形高的比为2:3:4:1,那么第二组频数是______.
武侯区某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据单位:分钟:10、12、15、8、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、若将这些数据以4为组距进行分组,则组数是_____组.
三、解答题(本大题共6小题,共54.0分)
七年级320名学生参加安全知识竞赛活动,小明随机调查了部分学生的成绩分数为整数,绘制了频率分布表和频数分布直方图不完整,请结合图表信息回答下列问题:
成绩分
频数
2
8
12
10
6
2
补全频数直方图;
小明调查的学生人数是______;频率分布表的组距是______;
七年级参加本次竞赛活动,分数x在范围内的学生约有多少人.
某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图.
这次抽样调查的样本容量是________,并补全条形统计图.
等级学生人数占被调查人数的百分比为_______,在扇形统计图中C等级所对应的圆心角为________.
该校九年级学生有1500人,请你估计其中A等级的学生人数.
垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某校举行一场学生在线参与垃圾分类处理知识测试满分100分,得分均为整数,学校从全校2800名学生中随机抽取部分学生的成绩,绘制成如图不完整的统计图表.
抽取的部分学生测试成绩的频数分布表
成绩分
频数人
百分比
10
15
n
m
40
15
由图表中给出的信息回答下列问题:
频数分布表中,_____,_____本次抽样调查的样本容量是_____.
补全频数分布直方图.
如果成绩在80分以上包括80分为优秀,估计该校本次测试成绩优秀的学生人数.
体育委员统计了全班同学60秒跳绳的次数,绘制出频数分布表和部分频数分布直方图,如图所示.请根据以下信息,解答下列问题:
次数x
频数
2
4
20
12
8
3
1
Ⅰ补全直方图;
Ⅱ全班有学生______名,频数分布表的组距是______,组数是______;
Ⅲ跳绳次数x在范围内的学生有______,占全班学生的百分之______。
某校八年级学生进行体育测试,八年级班男生的立定跳远成绩绘制成如图所示的频数分布直方图,图中从左到右各矩形的高之比是,最后一组的频数是6,根据直方图所表达的信息,解答下列问题.
该班有多少名男生?
若立定跳远的成绩在以上包括为合格,则该班的这项测试合格率是多少?
“微信运动“被越来越多的人关注和喜爱,某兴趣小组随机调查了某市50名教师某日微信运动中的步数情况并进行统计整理,绘制了如图的统计图表不完整,请根据以上信息,解答下列问题:
组别
步数万步
频
第1组
8
第2组
15
第3组
12
第4组
10
第5组
3
第6组
a
______,______;
补全频数分布直方图;
若该市约有40000名教师,估计日行走步数超过万步包含万步的教师约有多少名?
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查频数与频率,解题的关键是掌握频数之和等于总数、频率之和等于1,频率频数总数根据频率之和等于1求得第5组的频率,再由频数频率总数计算可得.
【解答】
解:第一组到第四组所占的百分比之和为,
第五组的所占的百分比之为,
则第五组的频数为.
故选B.
2.【答案】A
【解析】
【分析】
本题考查频率公式.根据频率公式:,频数频率总数,把频率,总数代入计算即可.
【解答】
解:,
频数频率总数.
故选A.
3.【答案】B
【解析】
【分析】本题主要考查条形统计图与频数分布直方图之间的关系,只要重点掌握其各自的特点,再加以区分即可解答,频数分布直方图条与条之间无间隔,而条形统计图有;条形统计图是用条形的高度表示频数的大小,而直方图是用长方形的面积表示频数,当长方形的宽相等的时候,把组距看成“1”,用矩形的的高表示频数;根据这些作判断即可.
【解答】
解:条形图是用条形的高度表示频数的大小,而直方图实际上是用长方形的面积表示频数,二者有很大的区别,故错误;
条形统计图各个“条形”之间有间隙,而频数分布直方图没有,故描述正确;
频数分布直方图用横轴表示考察对象数据的变化范围,用纵轴表示相应范围内数据的频数,故描述正确;
故选B.
4.【答案】C
【解析】
【分析】
本题主要考查了频数分布直方图,解答此题的关键是弄清频数分布直方图的横坐标与纵坐标表示的意义,解答此题根据频数分布直方图的意义解答即可.
【解答】
解:各小组的频率之和应等于1,故错误;
B.各小组的频数之和应等于总数据n,故错误;
C.各小组频数之和等于n,正确;
D.各小组的长方形高的和不是1,故错误.
故选C.
5.【答案】A
【解析】解:频率分布直方图的纵轴表示,
故选:A.
根据频率分布直方图中纵横坐标的意义即可得.
本题考查频率直方图中横纵坐标表示的意义.
6.【答案】D
【解析】
【分析】
此题考查了数据的获取方法,实验法.分别从不同的地方获取一定数量的实验数据,注意数学知识和生活实际的联系.
【解答】
解:为了调查不同面额纸币上的细菌数量与使用次数的关系,分别从银行、商店、农贸市场及医院收费处随机采集了6种面额的纸币各30张,得到数据,这种方法为实验法.
故选D.
7.【答案】C
【解析】
【分析】
本题考查扇形统计图的知识,比较简单,解答本题的关键是充分理解扇形统计图的特点,扇形统计图只能反应所占某个总体的百分比,不能判断具体数量.观察扇形统计图,扇形统计图反应了七、八年级男生参加各种课外活动的人数占总人数的百分比,不能具体判断不同年级参加某项课外活动的人数多少.
【解答】
解:由题意可得本题的各年级的男生人数无法确定,故不能确定七年级男生打乒乓球与八年级男生踢足球的具体人数.
所以C选项错误.
故选C.
8.【答案】A
【解析】
【分析】
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数最大值最小值组距计算,注意小数部分要进位.
【解答】
解:在样本数据中最大值为141,最小值为50,它们的差是,
已知组距为10,那么由于,
故可以分成10组.
故选A.
9.【答案】D
【解析】解:5月份通话次数中,通话时间不超过15分钟的所占百分比是,
故选:D.
根据表格可以得到总的频数和通话时间不超过15分钟的频数,从而可以求得通话时间不超过15分钟的百分比.
本题考查频数分布表,解题的关键是明确题意,找出所求问题需要的条件.
10.【答案】B
【解析】解:该校九年级1分钟仰卧起坐次数在次之间的学生人数大约是人,
故选:B.
用总人数乘以样本中仰卧起坐次数在次之间的学生人数占被调查人数的比例即可得.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
11.【答案】?
【解析】
【试题解析】
【分析】
本题考查了频数与频率,解题关键是知道各量之间的关系.
由步行的频数是13,骑车的频数是11,从而得到则乘车的频率.
【解答】
解:乘车的频率是:.
故答案为?.
12.【答案】10
【解析】解:一只不透明的袋子中装有红球和白球50个,摸到红球的频率是,
袋中有红球:个.
故答案为:10.
直接利用频率的意义进而分析得出答案.
此题主要考查了频率,正确理解频率的意义是解题关键.
13.【答案】24
【解析】解:.
故答案是:24.
频数分布直方图中,各个长方形的高之比依次为2:3:4:1,则指各组频数之比为2:3:4:1,据此即可求出第二小组的频数.
此题考查了频数率分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.
14.【答案】5
【解析】
【分析】
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数最大值最小值组距计算,注意小数部分要进位.则,所以组数为5.
【解答】
解:根据组数最大值最小值组距小数部分要进位
则
所以组数为5.
故答案为5.
15.【答案】40?
5
【解析】解:由频数分布表可知,
这一组的频数是6,
补全的频数分布直方图如右图所示;
小明调查的学生人数是:,
频率分布表的组距是,
故答案为:40,5;
人,
答:分数x在范围内的学生约有128人.
根据频数分布表中的数据,可以将频数分布直方图补充完整;
根据频数分布表中的数据,可以计算出小明调查的学生人数,再根据直方图中的数据,可以计算出组距;
根据频数分布表中的数据,可以计算出分数x在范围内的学生约有多少人.
本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
16.【答案】解:;
补全条形图如图所示:
;
;72;
该校九年级学生有1500人,
估计其中A等级的学生人数人.
【解析】
【分析】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
由A等级的人数和其所占的百分比即可求出抽样调查的样本容量;求出B等级的人数即可补全条形图;
用B等级的人数除以总人数即可得到其占被调查人数的百分比;求出C等级所占的百分比,即可求出C等级所对应的圆心角;
由扇形统计图可知A等级所占的百分比,进而可求出九年级学生其中A等级的学生人数.
【解答】
解:由条形统计图和扇形统计图可知总人数人,所以B等级的人数人,
故答案为50;
等级学生人数占被调查人数的百分比;
在扇形统计图中C等级所对应的圆心角,
故答案为;72;
见答案.
17.【答案】解:,,100;
由知,,
补全的频数分布直方图如图所示;
,
人.
答:估计该校本次测试成绩优秀的学生人数为1540人.
【解析】
【试题解析】
【分析】
本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
根据这一组的频数和所占的百分比,可以求得本次抽取的人数,然后即可计算出m、n的值;
根据中m的值,可以将频数分布直方图补充完整;
根据频数分布表中的数据,可以得到成绩为优秀的人数占被抽取人数的百分比,进而得解.
【解答】
解:随机抽取的学生总人数为:,
,
,
故答案为:20,,100;
见答案;
见答案.
18.【答案】解:Ⅰ在有4人,有8人,补全直方图如下:
Ⅱ,20,7;
Ⅲ人,64.
【解析】
【分析】
本题主要考查的是频数分布表和频数分布直方图的应用,能够从统计图和统计表中获取有效信息是解题的关键.
Ⅰ根据频数统计表可知跳绳次数在之间的频数是4,之间的频数为8,从而可补全直方图;
Ⅱ把所有的频数加起来得出全班学生数,再根据图表给出的数据即可得出频数分布表的组距和组数;
Ⅲ把数x在范围内的频数加起来得出次数x在范围内的学生数,再除以总数即可得出占全班学生的百分比.
解:Ⅰ见答案
Ⅱ全班有学生人,
频数分布表的组距是20;组数是7;
故答案为:50,20,7;
Ⅲ?根据题意得:
人,
则跳绳次数x在范围内的学生有32人;
占全班学生人数的百分比是:.
故答案为32人,64.
19.【答案】解:人,即该班有40名男生;
,即立定跳远的成绩在米以上包括米为合格,合格率是.
【解析】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
利用最后一组的频数所占的百分比八年级班男生人数;
用立定跳远的成绩在米以上的人数所占的比例和立定跳远的成绩在米以上包括米的合格率.
20.【答案】2?
16
【解析】,
第1组的占比为,因此.
故答案为:2,16.
画图如下:
根据题意:,和的总人数为:人.
占总人数的比例为:.
因此,全市日行走步数超过万步包含万步的教师约有:
人.
总共调查人数为50,因此,第1组的占比为.
根据求得的a的值画图即可.
需要先计算超过万步的占比,在计算人数.
本题是一道利用统计知识解答实际问题的重点考题,主要考查利用统计图表,处理数据的能力和利用样本估计总体的思想.解答这类题目,观察图表要细致,对应的图例及其关系不能错位,计算要认真准确.同时,解题方法要灵活多样,切忌死记硬背,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.
第18页,共18页
第17页,共18页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
